本文结合 代码随想录 + leetcode官方解答，做了学习和总结，仅个人记录学习。
代码随想录网址代码随想录
动态规划大致分为以下几个问题：
1.基础动态规划
2.背包问题
3.打家劫舍
4.股票问题
5.子序列问题
1.基础动态规划
基础使用场景：多为计算最少个数，返回一般为一个整数
解决基本思路：
1考虑前一个状态和该状态的影响关系（递推公式）
2注意起始状态（初始化）
3考虑遍历时需要的基础存储量（如数组，变量），决定了循环的层数
2.背包问题
2.1 01背包问题
2.1.1基础背包问题
问题：背包总承重量、物品重量+物品价值，每个物品最多取1次，求背包装载最大价值。
解法：二维数组，dp[i][j],i表示物品，j表示0-m（m为背包承受的最大重量），dp[i][j]表示j重量下前 i 个物品所能达到的最大价值。
横向遍历：前i个物品所能装载到该重量下的最大价值。
赋值：第i个物品在j重量下只有两个状态，要么装要么不装，所以只用对两个值比较选最大
不装：为dp[i-1][j]的值
装：为dp[i-1][j-w]的值
比较后取最大值。
结果：取dp[i][j]
eg.）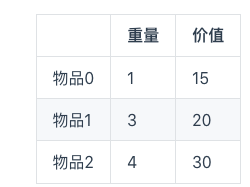
2.1.1变种背包
问题：从数据集中选出部分数，使这些数总和达到某个值n，数据集中的每个数最多取1次。
解法：二维数组，dp[i][j],i表示数字，j表示0-n（n为到达值），dp[i][j]表示j数值下前i个数是否能
到达该值，为bool。
关键不同点为dp[i][j]为bool值，核心为是否能到达这个值。
判断方式和01背包相同，要么取值，要么不取值。
即 取：dp[i-1][j-n[I]]为true，则为true
不取：dp[i-1][j]为true，则为true
优化：
dp[0] = truefor _, weight := range stones {for j := m; j >= weight; j-- {dp[j] = dp[j] || dp[j-weight]}}目标和中，dfs可以解决，但复杂度高。考虑前一状态是否会影响到现状态，发现确实有影响，再考虑变化情况：
图片摘自力扣
因为数组下标从0开始，所以对整个数组计数进行了偏移，即向右平移sum个单位。
把数值变量变化为了数组，比如之前的是0，1，2，3，现在变为了[0,0],[0,1],[1,0]...[5,3]
总结：
背包一般能解决的问题：
（1）能到达的最大值（返回int）
（2）是否能到达该值（返回bool）
（3）到达该值的种数（返回int）
2.2 完全背包
和01背包问题相比，物品选择的次数是0次和多次。其余部分和01背包问题来说没有什么大差别。
新物品放入最新状态，可以影响后一状态，体现在循环的时候可以从小到大遍历。
下题中，排列顺序影响数值结果，考虑递推规律：
以4为示例：
最后一次选1，则为剔除选择1的所有情况，到达4-1=3的所有情况
最后一次选2，到达4-2=3的所有情况
最后一次选3，到达4-3=1的所有情况
则4的所有可能性为，dp[3]+dp[2]+dp[1]
比较最小情况，初始化赋值为amount+1
通过是否达到下标进行问题转换。 
3打家劫舍系列
4股票系列
121. 买卖股票的最佳时机
122. 买卖股票的最佳时机 II
714. 买卖股票的最佳时机含手续费
123. 买卖股票的最佳时机 III
188. 买卖股票的最佳时机 IV
309. 最佳买卖股票时机含冷冻期
如 5位置，持有状态即要么买要么不买，买为-5，不买为原值-1
不持状态即要么卖要么不卖，卖为5-1，不卖为0.
均取最大值保存
其实也类似贪心，持有的时候保存最小买入值，卖出的时候保存最大卖出值。
第一题仅能卖一次，第二题能够卖多次，所以主要不同为，卖的过程中必须把之前买的卖掉才能购买。
买卖多次状态中再增加一个交易费用，即卖出状态下-fee
设置四个状态，第一次买入，第一次卖出，第二次买入，第二次卖出。
第一次买入选价格最低点；第一次卖出为当前价格+第一次买入价格；第二次买入为第一次卖出持有收益-当前价格；第二次卖出为当前价格+第二次买入持有收益。
和上一题相比，唯一的不同是次数限制不止为两次，交易一次，分为买入/持有，卖出/持有两种状态，所以状态数增加到2*k种，为增加普适度，添加dp[0]=0状态。
出现冷冻状态，增加冷冻状态、非冷冻持有状态。
买入状态的值影响的有：冷冻状态买入、非冷冻状态买入、原买入状态
卖出状态：买入状态+物价
非冷冻持有状态值变化：原非冷冻、冷冻
冷冻状态：买入状态。
5子序列问题
300. 最长递增子序列详解
感觉上面的链接讲得很细，贴一个
因为同一个字符只能算一个，所以需要和斜对角的数进行比较ˇ
视频图解 动态规划 最长公共子序列
换了个描述，解法和上一题完全一致
连续子数组转换为二维数组，需要和斜对角数进行比较。
和不相交的线 、最长公共子序列解法一致。
做多了动态规划可能会被某几个定式给框住，这时候需要会归到最简单的情况，从一两个字符开始分析问题，并且把所有方案给列出来进行思考。
上题的详细解析编辑距离图解
上述为暴力解法
上述为动态规划解法
