前缀树

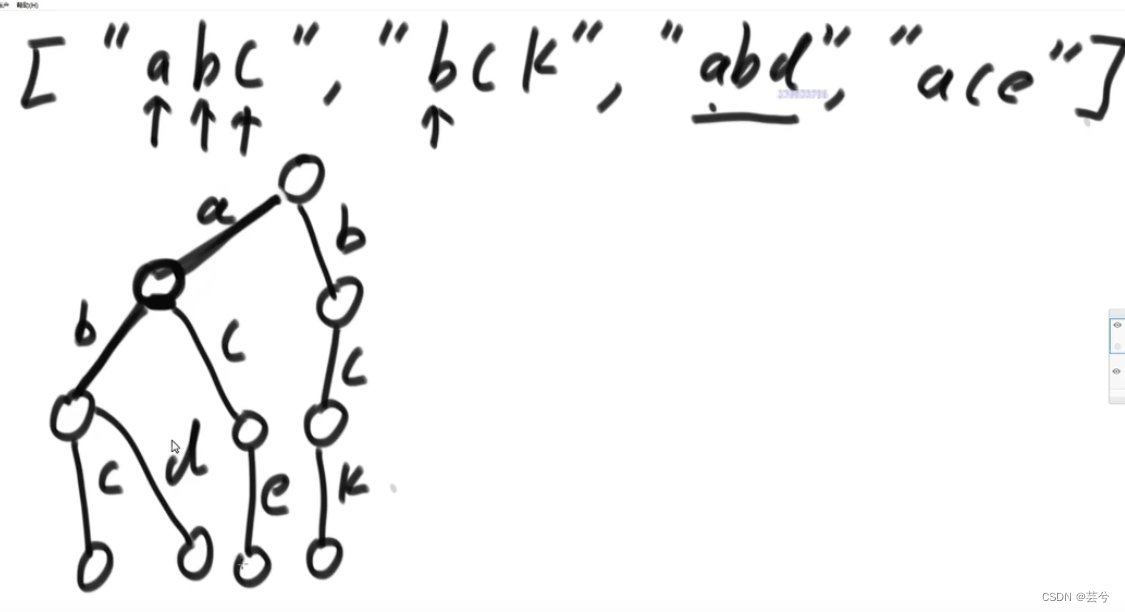
通常为了使用方便，会构造一个结点，丰富结点信息。

class TrieNode{
public:int pass; // 该节点被通过的次数int end; // 以该节点为终点的节点的个数vector<TrieNode> nexts; //该节点下边的节点TrieNode() {pass = 0;end = 0;nexts = new vector<TrieNode>(26);}
}

通过pass和end两个值，可以很方便的查询前缀树以某个字段为前缀的字符串数。

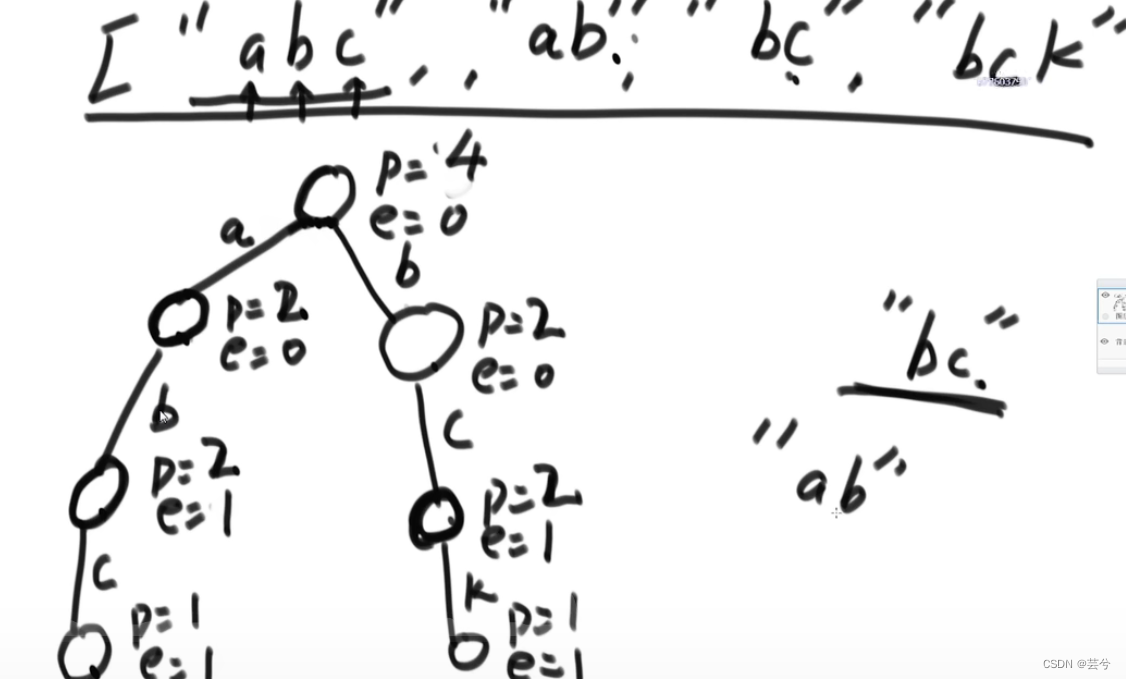
构造前缀树的过程：

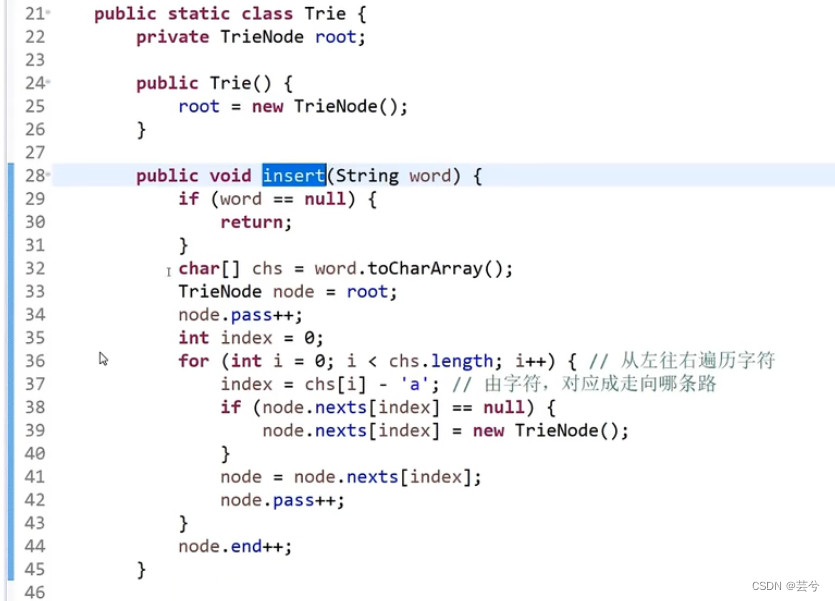
根据前缀树搜索一个Word加入了几次：
将word中每个字母遍历完，如果遍历过程中发现next为空，表面该Word没有插入过，否则可以完成遍历，遍历完成时的节点的end值就是所求。

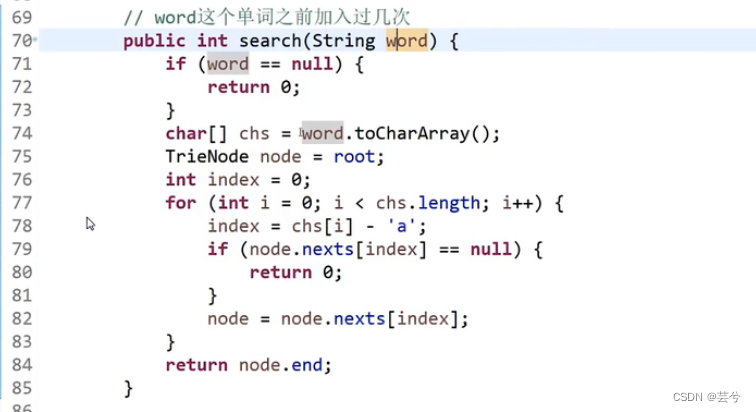
同理根据前缀树搜索一个前缀pre的次数，如果不能完成遍历（遍历到空值）则表面没有插入过，否则返回遍历完成时的节点的pass值。

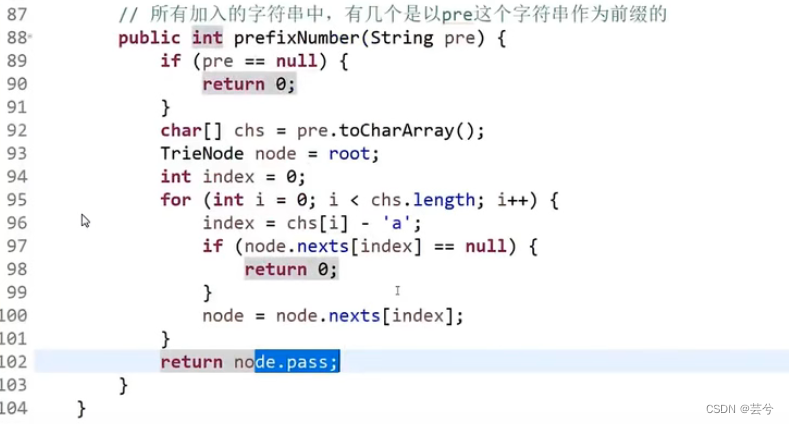
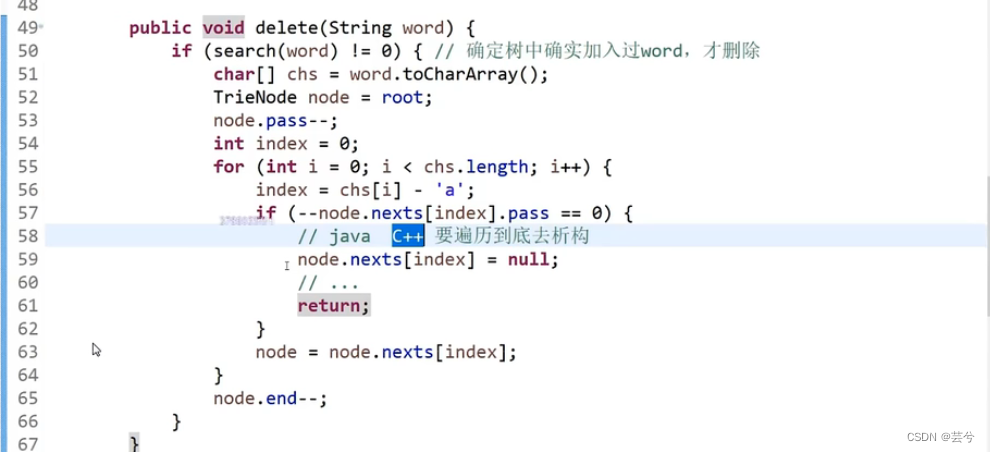
删除某个Word的过程：
首先执行搜索Word，确认Word有被插入后，遍历该Word，将所经过的节点pass–，遍历结束时的节点还需end–。特殊地，当pass–过程中发现pass已经减为0，则该节点后边的节点都需要删除掉，即在之后的遍历过程中直接手动删除每个节点，由于直接删节点会导致无法遍历这个节点后边的节点，因此需要记录下要删的节点，可以存放在栈中，遍历完成时。再遍历一次栈，一个个删除栈中的节点。

贪心算法

有限时间完成最多次的会议

有限时间内安排完成最多次的会议
思路，先根据会议结束的时间进行排序，然后按照会议结束的时间最早的先安排。
代码实现，先设置一个比较器，根据结束时间比较。

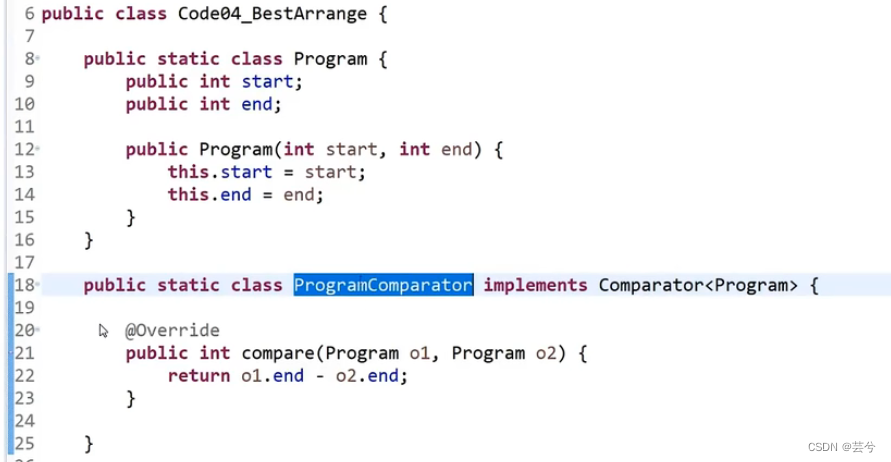
真正安排会议时：
先判断根据排好的顺序遍历会议，如果会议开始的时间在设置的时间timePoint前，则进行会议安排，result++，并将时间点timePoint设置为该会议的结束点。

最省钱的切割金条方法

比较经典的哈夫曼编码问题
将数组中的数据构成小根堆，每次取出小根堆头两个数的结合值sum，代码增加sum，将sum再插入小根堆，再取小根堆头两个数，直至小根堆中只有一个数。

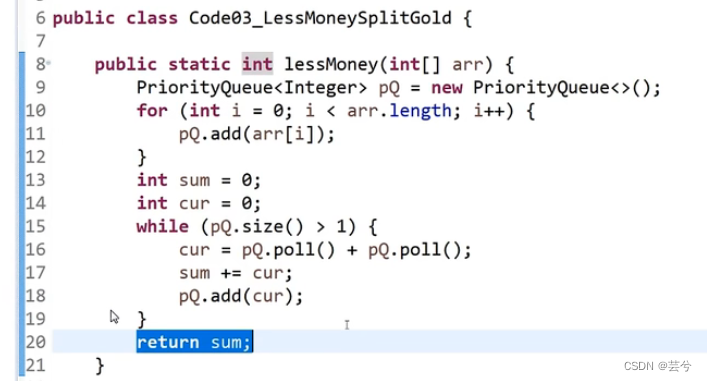
赚钱最多的项目安排方案

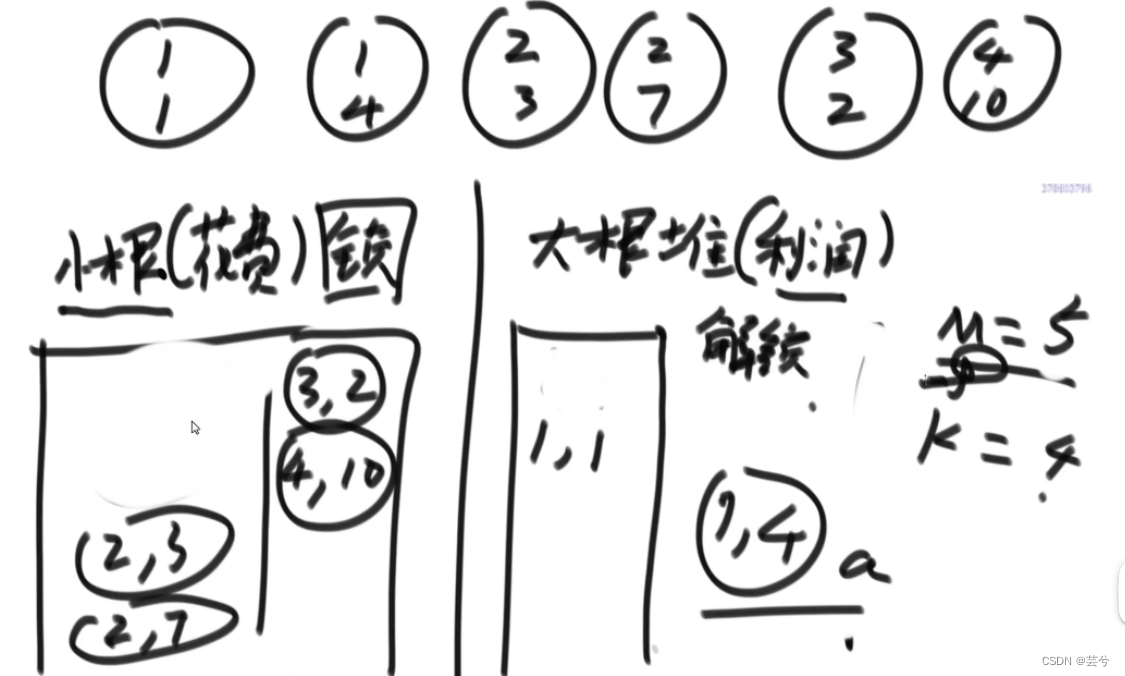
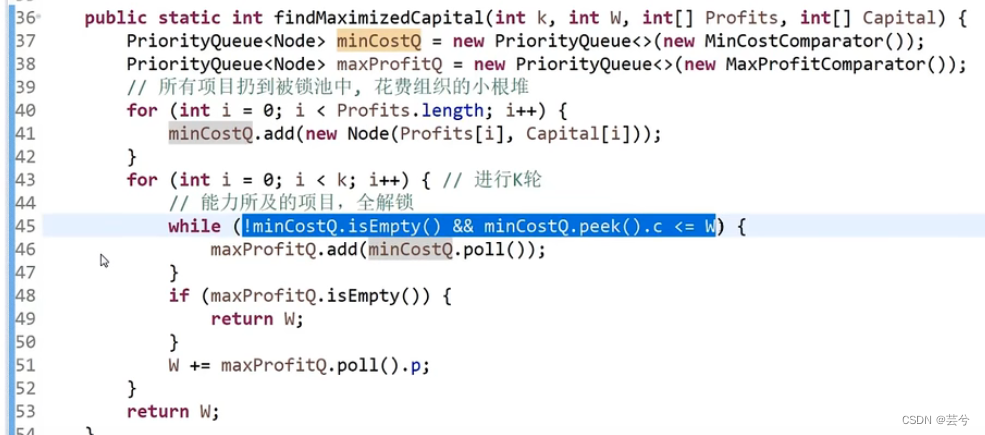
每个项目（上边代表项目需要的投入资金，下边代表项目获取的净利润值）。启动资金是1，如何安排项目能够最快获取利润。
思路：
将项目按照投入资金存入小根堆，弹出投入资金≤当前资金的项目（解锁的项目），将解锁的项目按照利润存入大根堆，每次弹出利润最大的项目，将当前资金累加上弹出项目的利润值。

字典序比较方法

字典序就是字典中单词排列的顺序。
如果两个单词长度一致，将单词看做27进制数比较大小，如果两单词长度不一致，将短的单词尾用0补全为长单词一样的长度，然后比较大小。

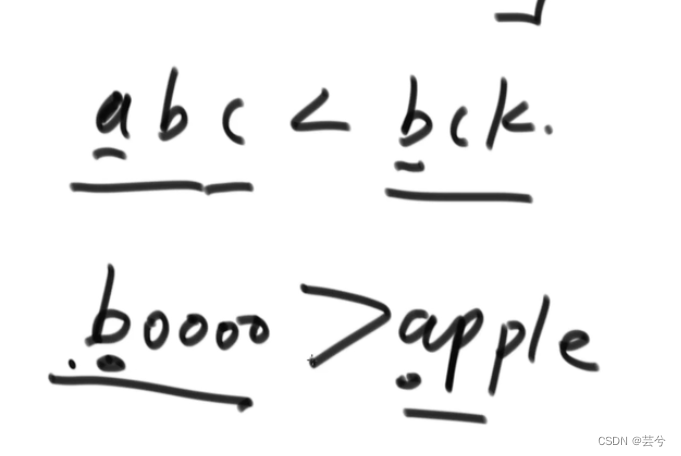
一个数据流中随时可以取得中位数

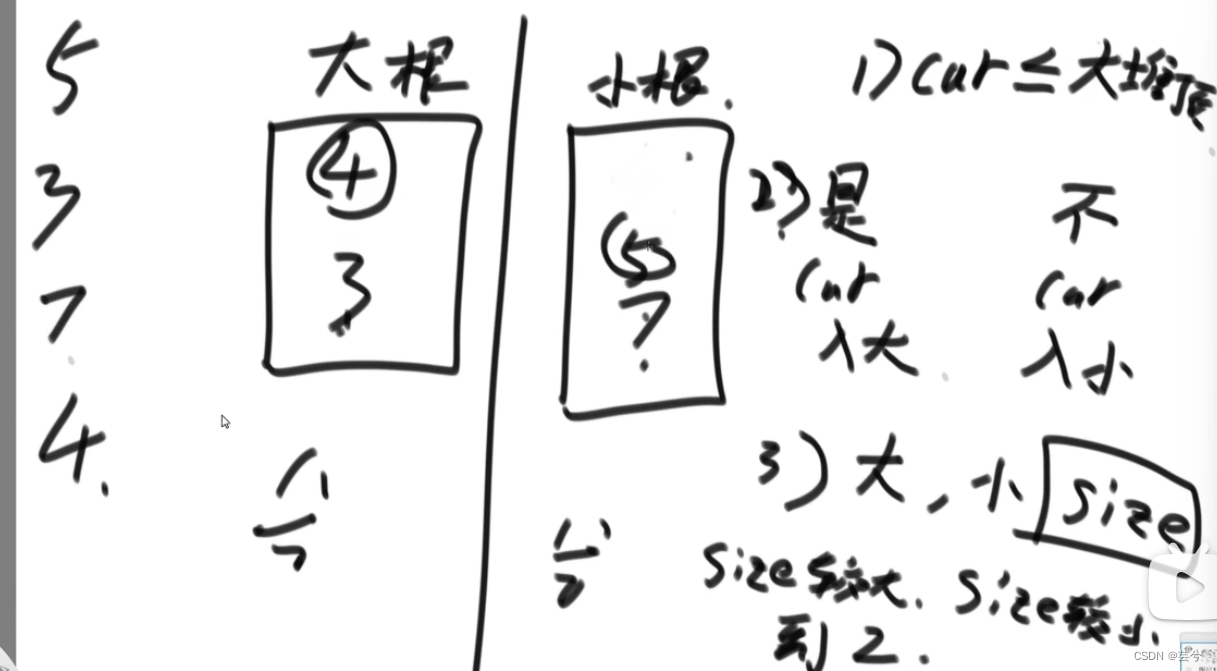
• 准备一个大根堆和一个小根堆。
• 第一个数进大根堆。
• 后边的数，如果值≤大根堆头，入大根堆，如果小，入小根堆。
  比较两个堆的大小，如果两个堆的大小相差＞2，则将较大的堆中堆头弹出，插入长度较小的堆中去。
• 在这种规则下，大根堆的头是大根堆最大的数，小根堆的头是小根堆中最小的数，而根据规则，小根堆中的数都大于大根堆，且两个堆的大小不超过1，因此，大小根堆的堆头就是数据流中最中间的两个元素。
• 如果两个堆的大小之和为奇数，那么较大的那个堆的头结点就是中位数，如果两个堆的大小之和为偶数，那么两个堆的头结点的平均数就是中位数。
  

N皇后问题

record数组用于表示第i行的皇后放到了第几列，i就是数组下标，对应的值代表放到列号。
递归体process1，输入参数依次是

• 当前排列到第几行
• record记录数组
• 整体要排多少个
• 返回值是合理的排列方法总数。

假如能来到第n行，说明找到一种有效排列，返回1.
非第n行，则需判断当前行的皇后放到1-n中的那一列上是有效的。如果有效，则更新record，继续process1处理（第i+1行的皇后）。

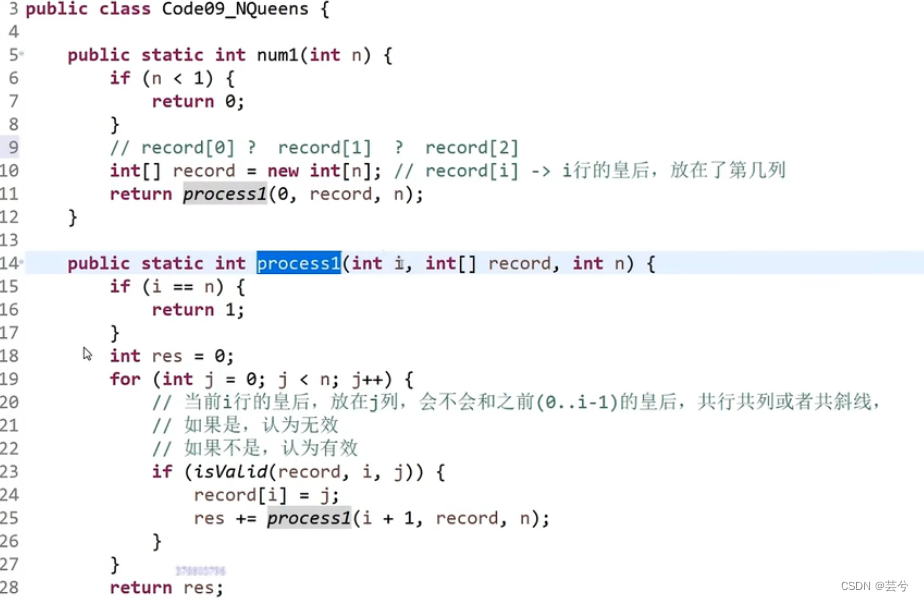
关于判断是否有效 isValid（record, i, j）。
record记录，第i个放到第j列。
首先由于是按行遍历，行号必不相同，故只需判断是否共列和共斜线 。
共列：判断列号j是否与之前record中的元素值相同
共列：判断两皇后所为位置连线斜率是否为45°或者135°，即列号相减的绝对值是否等于行号相减的绝对值。

/*
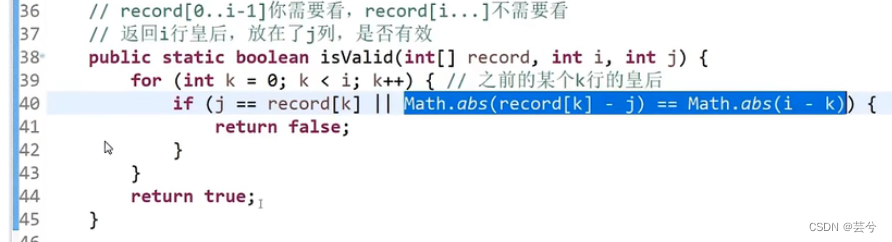
* 8皇后问题，在方形棋盘摆皇后，皇后不同行，不同列，不共对角线输入 n，代表给定n行n列的棋盘
返回所有解法的solution数组，solution
eg1:输入：n = 4输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]解释：如上图所示，4 皇后问题存在两个不同的解法。
eg2:输入：n = 1输出：[["Q"]]
*/ // 在已有queen数组基础上判断，将第i行的j列放置皇后是否符合规格
// queen数组是对解法的记录，他的索引代表行号，而值代表当前行皇后所在的列号
bool isValid(vector<int>& queen, int i, int j) {for (int k = 0; k < i; k++) {if (queen[k] == j || abs(queen[k] - j) == abs(i - k)) {return false;}}return true;
}// 根据queen数组转为要求的棋盘输出
vector<string> generateBoard(vector<int> & queen) {int n = queen.size();  // 获取棋盘长度auto board = vector<string>(); // 结果是字符串数组for (int i = 0; i < n; i++) {string row = string(n, '.');row[queen[i]] = 'Q';board.push_back(row);}return board;
}// 递归尝试解法
// i代表当前尝试到第i行，queen是当前记录的数组
void queenRecursion(int i, vector<vector<string>> &solution, vector<int> &queen) {// 能来带到第n行，表示已经得到可行解，将queen转为board数组压入解法数组solutionint n = queen.size();if (i == n) {solution.push_back(generateBoard(queen));}else {// 否则一个一个尝试将第i行的j列放上皇后是否有效for (int j = 0; j < n; j++) {if (isValid(queen, i, j)) {queen[i] = j;queenRecursion(i + 1, solution, queen);}}}return;
}// 8皇后递归调用入口
vector<vector<string>> eightQueens(int n){auto solution = vector<vector<string>>();auto queen = vector<int>(n, -1);queenRecursion(0, solution, queen);return solution;
}

位运算优化的N皇后问题

只能处理不超过32位。
用一个二进制数来表示皇后放置的位置。
limit的含义是将一个数后n位赋值为1，其他为0，以此用于限制设置位运算的范围。

判断皇后位置是否合法可以通过位运算优化。
依旧是只考虑共列和共斜线的情况，共斜线分为左斜线与右斜线。三种情况求或就是所有可以排除的情况。
这三种情况可以直接通过某个皇后所在位置，左移、右移来确定。

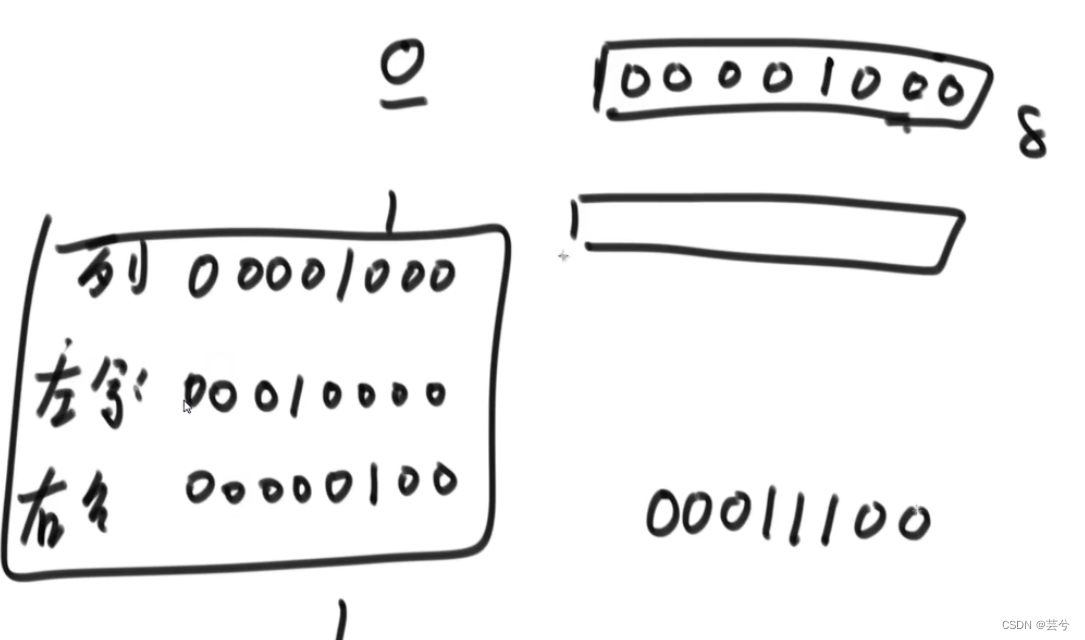
递归体process2（）函数
输入参数：

• 位限制limit
• 列限制colLim
• 左对角限制leftDiaLim
• 右对角限制rightDiaLim

当列限制与位限制相同时，表示有效位上都填上了皇后，找到一种合理的方法。

将所有限制情况取或，得到所有限制的位置，取反后，1的位置代表可以放的位置，再与位限制limit求与运算得到pos，pos中1的位置代表的就是可以插入的位置。

当pos不为0，代表还有可以放置的位置，从最右侧的1开始放置，放置后，更新pos，pos = pos - mostRightOne。更新三种限制，继续递归。
列限制为原有限制与mostRightOne的或，左右对角线的限制为原有限制与mostRightOne或运算后在左右移位。
注意：左右对角限制对一行的限制是左右移位的地方，但对于再下一行需要接着左右移位。因此这里是左右对角限制DiaLim先与mostRightOne求或运算后，整体左右移位。如果定式思维，先mostRightOne左右移位再与DiaLim求或这就是刻舟求剑了。因为对于第一行所需的皇后，对角限制使得第二行相应列左右移位1次被限制，而对第三行的限制是第一行列对应位置左右移位2次被限制，即移位操作是累积进行的，必须得是先或再移位，才能体现出改行移位1次，而上一行会多移位一次。

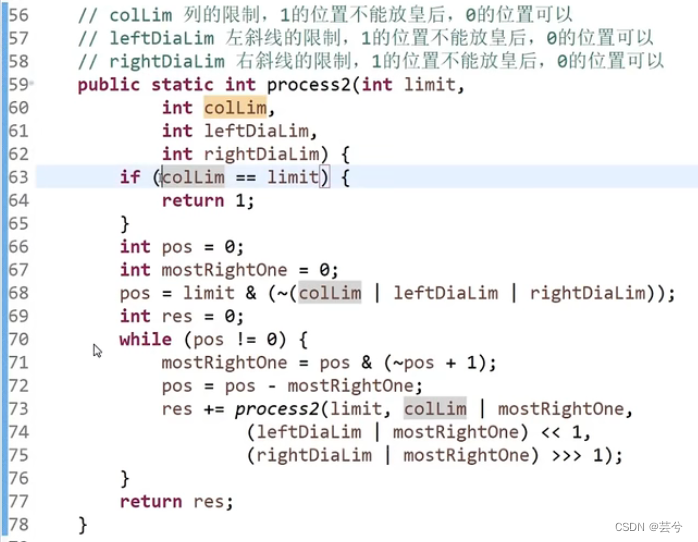
汉诺塔问题

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
示例1:

输入：A = [2, 1, 0], B = [], C = []
输出：C = [2, 1, 0]
示例2:

输入：A = [1, 0], B = [], C = []
输出：C = [1, 0]
（还有的题目要求移动的步数）

/*
在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
eg1:输入：A = [2, 1, 0], B = [], C = []输出：C = [2, 1, 0]eg2:输入：A = [1, 0], B = [], C = []输出：C = [1, 0]
*/// 问题拆解将A中除最大元素外的n-1个先放到B，将A最大的元素放到C，再将B中的n-1个元素放到C
void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {moveDisk(A.size(), A, B, C);
}void moveDisk(int n, vector<int>& A, vector<int>& B, vector<int>& C) {if (n == 1) {C.push_back(A.back());A.pop_back();return;}else {moveDisk(n - 1, A, C, B); // 将A的后n-1个移动到BC.push_back(A.back()); //将A中最大的放到CA.pop_back();  // A弹出最大moveDisk(n - 1, B, A, C); // 将B中n-1个移动到C}
}

打印一个字符的全部子序列

/*
打印一个字符串的全部子序列，包含空字符串
输入字符串str
*/// 思路从空开始（i=0， i指示子序列对于字符的选择来到第i个字符）构建子序列，每个字符要或不要两种选择
void recuseSubsquence(int i, string str) {if (i == str.length()) {cout << str;}// 保留当前字符的递归recuseSubsquence(i + 1, str);// 记录下当前字符char tmp = str[i];// 将当前字符设置为0,代表的字符为null即''，则这里相当于暂时删去了当前字符str[i] = 0;// 这里是不保留当前字符的递归recuseSubsquence(i + 1, str);// 还原字符串str[i] = tmp;
}void printAllSubsquence(string str) {recuseSubsquence(0, str);
}

获得字符串的全排列

/*
全排列
给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：
输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：
输入：nums = [1]
输出：[[1]]
*/// 思路：用i指示排列中字符数，从i=0（空字符串）开始构建排列，i前边是已经选择好的字符，不动
//，i的位置上，i后边的每个字符都有可能放置，通过交换的方式放置，再交换回去，当i的长度为
// 排列长度时获得排列，压入ans中void swap(vector<int>& arr, int i, int j) {int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;
}void getPermute(int i, vector<vector<int>> &ans, vector<int> &permutation) {if (i == permutation.size()) {ans.push_back(permutation);}for (int k = i; k < permutation.size(); k++) {swap(permutation, i, k);getPermute(i + 1, ans, permutation);swap(permutation, i, k);}
}vector<vector<int>> permute(vector<int>& nums) {auto ans = vector<vector<int>>();getPermute(0, ans, nums);return ans;
}

两聪明人玩牌

先手拿牌得分函数由f(arr, L, R)计算，后手由s(arr, L, R)计算。
先手情况下，当牌只剩一张（L==R）return arr[L]
否则决策是 arr[L] + s(arr, L+1, R)或者 arr[R] + s(arr,L, R-1)中的较大值

后手函数s(arr, L, R)
当L ==R时，return 0；
否则决策是
f(arr, L+1, R) 和f(arr, L, R-1)中的较小值。
因为是后手，所以别人一定在选择L和R时令自己的先手是最小的结果。

/*
整型数组arr代表不同纸牌排成一线，两玩家A和B轮流取牌且只能取数组左右两头的牌
规定A先B后，谁拿的牌大谁获胜，返回获胜者的分数。A和B都是聪明人。
eg1：
arr = [1, 2, 100, 4]
A会先拿1以保证B拿不到100，最终，A得1 + 100， B得4 + 2
return 101
eg2：
arr = [1, 100, 2]
A得 2 + 1
B得 100
return 100
*///先手拿牌得分函数由f(arr, L, R)计算，后手由s(arr, L, R)计算。
//先手情况下，当牌只剩一张（L == R）return arr[L]
//否则决策是 arr[L] + s(arr, L + 1, R)或者 arr[R] + s(arr, L, R - 1)中的较大值
//
//后手函数s(arr, L, R)
//当L == R时，return 0；
//否则决策是
//f(arr, L + 1, R) 和f(arr, L, R - 1)中的较小值。
//因为是后手，所以别人一定在选择L和R时令自己的先手是最小的结果。int redHand(vector<int>& arr, int L, int R);// 黑方，后手函数
int blackHand(vector<int> &arr, int L, int R) {if (L == R) {return 0;}int Lscore = redHand(arr, L + 1, R);int Rscore = redHand(arr, L, R - 1);return min(Lscore, Rscore);
}// 红方，先手函数
int redHand(vector<int>& arr, int L, int R) {if (L == R) {return arr[L];}int Lscore = L + blackHand(arr, L + 1, R);int Rscore = R + blackHand(arr, L, R - 1);return max(Lscore, Rscore);
}int winnerScore(vector<int>& arr) {if (arr.size() < 1) {return 0;}int red = redHand(arr, 0, arr.size());int black = blackHand(arr, 0, arr.size());return  max(red, black);
}

不借助额外数据结构逆序一个栈

先定义一个函数eraseLast()，移除并返回栈底元素，并维持栈中其他元素不变。

int eraseBottom(stack<int>& stk) {int top = stk.top();stk.pop();if (stk.empty()) {return top;}else {int bottom = eraseBottom(stk);stk.push(top);return bottom;}
}

根据上述取底的过程，可以递归来逆序栈。
不停的取底，直至栈为空，将取到的底压回栈中。栈为空时结束，第一个压回的元素实际上是是最后一次求的栈底，实际上是栈顶元素，由此实现了逆序。

stack<int> reverseStack(stack<int>& stk) {if (stk.empty()) {return;}int bottom = eraseBottom(stk);reverseStack(stk);stk.push(bottom);
}

数字字母编解码

思路：从左到右尝试解码，i表示当前来到第i个字符，假定i前边已经解码完成，先考虑i位置。
假如i位置为0，则return0 ，因为没有以0开头对应的字母。若i位置属于[3, 9]，则只能将i位置单独解码。若i位置属于[1, 2]，i为1时，既可以i位置单独解码，也可i位置与i+1合起来解码，若i位置为2，i+1位置如果属于[0,6]也是可以i位置和i+1位置两位一块解码，否则只能单独解码。

/*
decodeAlphabet
1-A, 2-B, 3-C …… 26-Z，给定数字组成的字符串str，返回str的字母解码方式数目
*/// 给定的数字字符串str，解码到第i位
int decodeRecursion(string str, int i) {if (i == str.length()) {return 1;}if (str[i] == '0') {return 0;}if (str[i] == '1') {int res = decodeRecursion(str, i + 1); // i单独解码if (i + 1 < str.length()) {// 假定i+1还不越界，可以i与i+1两位编码res += decodeRecursion(str, i + 2);}return res;}if (str[i] == '2') {int res = decodeRecursion(str, i + 1); // i位单独解码if (i + 1 < str.length() && (str[i+1] >= '0' && str[i+1] <= '6')) {// 假定i+1还不越界，且i+1位范围在[0-6],可以i与i+1两位编码res += decodeRecursion(str, i + 2);}return res;}// i为[3,9] 只能i位单独解码return decodeRecursion(str, i + 1);
}// 递归入口
int decodeAlphabet(string str) {return decodeRecursion(str, 0);
}

回溯算法

回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

回溯三部曲

以题目为例：
LeetCode39
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。
对于给定的输入，保证和为 target 的不同组合数少于 150 个。
示例 1：
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。
示例 2：
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3：
输入: candidates = [2], target = 1
输出: []

确定参数

从零构建一个组合，需要一个临时的path
最终包含所有可能的结果ans
剩余还要满足的目标值left
循环起始位置startIndex
组合问题中一般需要startIndex，避免重复的情况

确定终止条件

left为0时终止找到一个
left <0 时终止无效解

单层搜索与回溯

每次可以从candidates的startIndex开始选择元素，由于可以重复选择，因此每次选择后，startIndex也不必+1.
注意再次递归时需要将startIndex修改为i，避免重复选择，例如前边选择1 ，再选7， 而选了7， 则不可再选1.

void combinationSumBack1(int index, int left, vector<int>& cadidates, vector<int>& path, vector<vector<int>>& ans) {if (left == 0) {ans.emplace_back(path);}for (int i = index; i < cadidates.size(); i++){if (left - cadidates[i] >= 0 ) {path.push_back(cadidates[i]);combinationSumBack1(i, left - cadidates[i], cadidates, path, ans); // 这里需要将startIndex修改为ipath.pop_back();}}
}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector<vector<int>> ans;vector<int> path;combinationSumBack(0, target, candidates, path, ans);return ans;
}

利用回溯算法解决组合、子集、排列、分割与棋盘问题

组合

力扣题目77
给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

组合情况分支树如下：

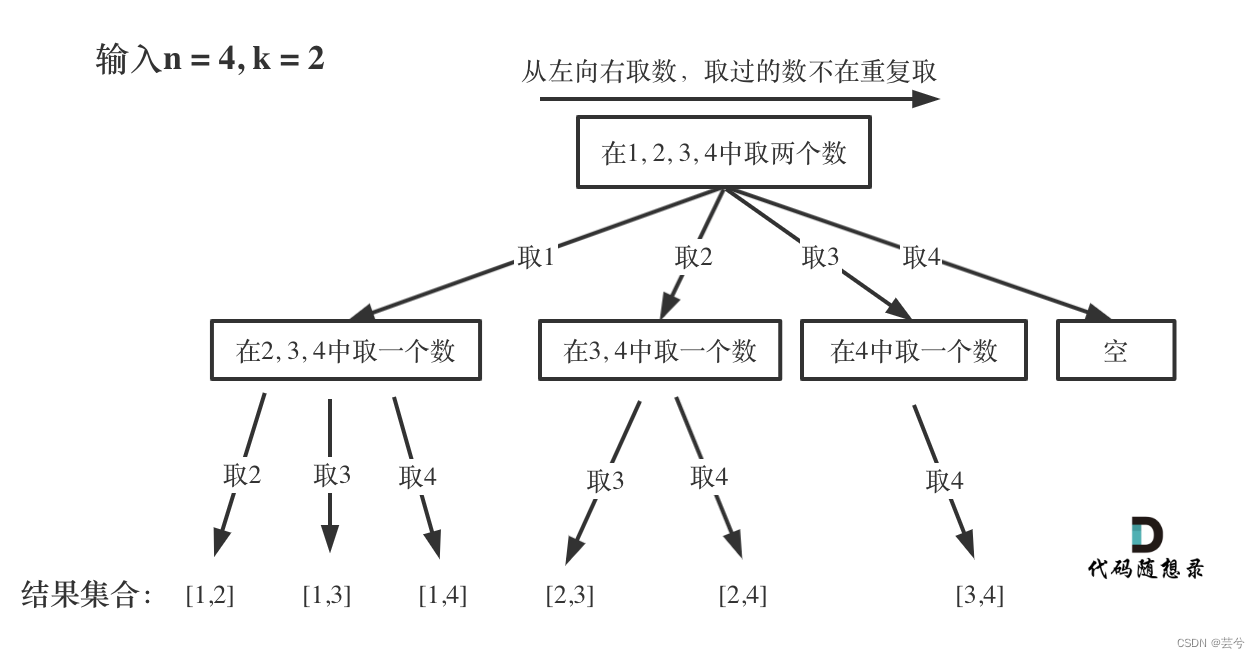
从图上可以看出组合问题我们会设置一个start，来控制数选择的范围，避免下一层选择时选到上边一层已经选过的元素。
第0层，start为0，故第0层可以选择的数为1,2，3,4
第1层，start为所选的元素，只能在所选元素右侧范围内继续选取。

确定参数

需要start确定组合数选择的左边界
需要index确定树的深度，即多少个数的组合
需要ans, path, 题目固定参数

终止条件 && 单层遍历

当所在分支来到深度为k时停止。

    if (path.size() == k) {ans.push_back(path);return;}

每层遍历时，path的当前可选节点为start开始的右边的每个元素
故本来for循环从start开始，到n结束
但是这里可以利用好k来剪枝，减少路径搜索。
因为下一层每次只能从i往后选择，最终需要k个数，假如某个时刻当前路径长度为path.size()，还需要k - path.size()个数，因此i右边至少还需要有k - path.size()
可供选择才可能有正解。故终止条件可以设置为
i <= n - (k - path.size()) + 1

void combineBacktracking(int index, int left, int n, int k, vector<int>& res, vector<vector<int>>& ans) {if (index == k) {if (res.size() == k) {ans.push_back(res);}return;}for (int i = left; i <= n - (k - res.size()) + 1; i++){res.push_back(i);combineBacktracking(index + 1, i + 1, n, k, res, ans);res.pop_back();}
}

子集

LeetCode78.子集
给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。
示例: 输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

确定参数

子集相对于组合，子集选择情况树中所有的节点，而组合只取叶子节点。

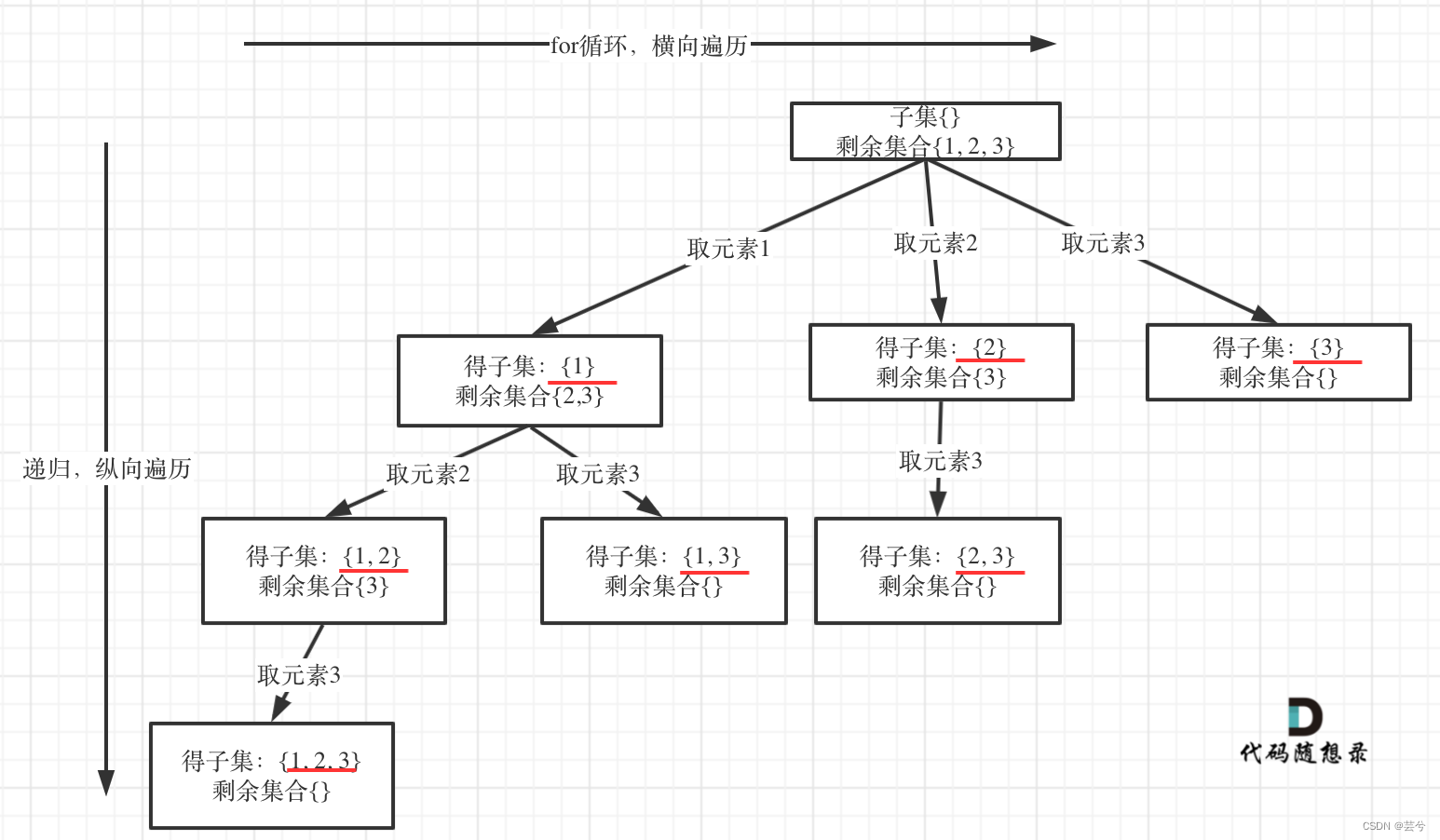
思路

每次递归都将当前的path添加到最终的ans中，依旧是用start参数，避免重复选择的问题。

void subsetsBacktracking(int start, vector<int> &nums,vector<int> &path, vector<vector<int>> &ans) {ans.emplace_back(path);for (int i = start; i < nums.size(); i++){path.push_back(nums[i]);subsetsBacktracking(i + 1, nums, path, ans);path.pop_back();}
}vector<vector<int>> subsets(vector<int>& nums) {vector<int> path;vector<vector<int>> ans;subsetsBacktracking(0, nums, path, ans);return ans;
}

子集去重

LeetCode90
给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。
示例:
输入: [1,2,2]
输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]

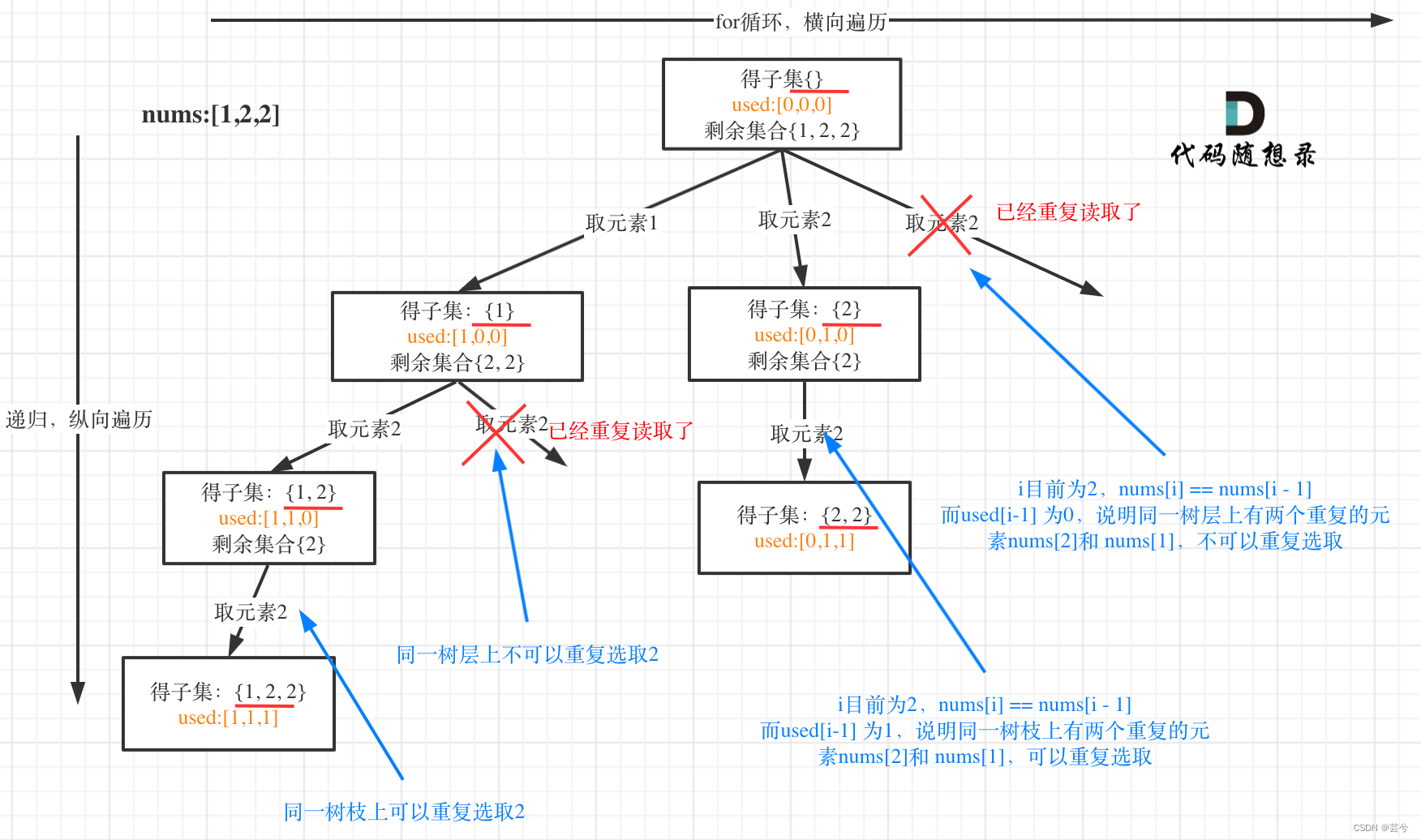
子集与组合的去重都是类似的，当同一层选择了同样的元素时，则后续就可能出现重复的组合或者子集，但是在纵向上，则可以允许有重复的元素

通用去重技巧：used数组

为避免重复，在每一层中使用set，记录填入path的元素，每次填入前检测set中是否已经有该元素，如果有直接跳过。
unordered_set<int> uset;定义在for循环外部，每层重置，每层中选取元素时，先判断uset中是否已经有元素了，如果有则跳过，如果该层没有选择过该元素，则path选择该元素，并将该元素填入到该层的uset中。

void subsetsWithDupBacktracking(int start, vector<int> &path, vector<int> &nums, vector<vector<int>> &ans) {ans.emplace_back(path);unordered_set<int> uset;for (int i = start; i < nums.size(); i++){if (uset.find(nums[i]) != uset.end()) {continue;}path.push_back(nums[i]);uset.insert(nums[i]);subsetsWithDupBacktracking(i + 1, path, nums, ans);path.pop_back();}
}

更快的去重

一种比较巧妙的做法是先对原有元素进行排序，将重复的元素放在一块：

sort(nums.begin(), nums.end());

在每层的for循环中添加：

  if (i > start && nums[i - 1] == nums[i]) {continue;}

这里的i > start && nums[i - 1] == nums[i]条件值得好好体会：
nums[i - 1] == nums[i]说明遇到了重复出现的元素，而i > start的限制保证了该层第一个重复的元素不会被 跳过，因此在纵向上允许选择一个重复元素，而在横向上，即每一层中不可再选择重复元素。

void subsetsWithDupBacktracking(int start, vector<int> &path, vector<int> &nums, vector<vector<int>> &ans) {ans.emplace_back(path);for (int i = start; i < nums.size(); i++){if (i > start && nums[i - 1] == nums[i]) {continue;}path.push_back(nums[i]);subsetsWithDupBacktracking(i + 1, path, nums, ans);path.pop_back();}
}vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end());vector<int> path;vector<vector<int>> ans;subsetsWithDupBacktracking(0, path, nums, ans);return ans;
}

这种使用数组去重的技巧需要先对数据进行排序，将重复元素放置在一起，然后通过允许每层中第一个元素出现相邻相等，其他元素不许相邻相等，从而实现了快速的去重。
但是这种方法在子序列题目中是不可以的！！！ 因此通用技巧更需要关注！！！

子序列

LeetCode491. 递增子序列
给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。
示例 1：
输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
示例 2：
输入：nums = [4,4,3,2,1]
输出：[[4,4]]

子序列是指每个元素都来自原序列，且元素直接的相对顺序保证不变
实际上，子序列可以看做是原序列num随机删除x（ 0<= x < num.size()）个元素后所得的序列

因为要保证相对顺序不变，而排序则会打乱原始顺序，故排序再利用数组去重的方法这里不可取，只能使用通用技巧，每层使用set来去重。
此外，这里要求是递增子序列，故如果发现不满足递增的情况，也需要跳过，判断是否递增：
取path最后一个元素，根据当前元素与其大小判断是否符合递增规则。

        if (path.size() > 0 && path[path.size() - 1] > nums[i]) {continue;}

void subsequencesBacktracking(int start, vector<int> &nums, vector<int> &path, vector<vector<int>> &ans) {if (path.size() > 1) {ans.emplace_back(path);}unordered_set<int> uset;for (int i = start; i < nums.size(); i++){if (path.size() > 0 && path[path.size() - 1] > nums[i]) {continue;}if (uset.find(nums[i]) != uset.end()) {continue;}uset.insert(nums[i]);path.push_back(nums[i]);subsequencesBacktracking(i + 1, nums, path, ans);path.pop_back();}
}vector<vector<int>> findSubsequences(vector<int>& nums) {vector<int> path;vector<vector<int>> ans;subsequencesBacktracking(0, nums, path, ans);return ans;
}

排列

LeetCode46.全排列
给定一个 没有重复 数字的序列，返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

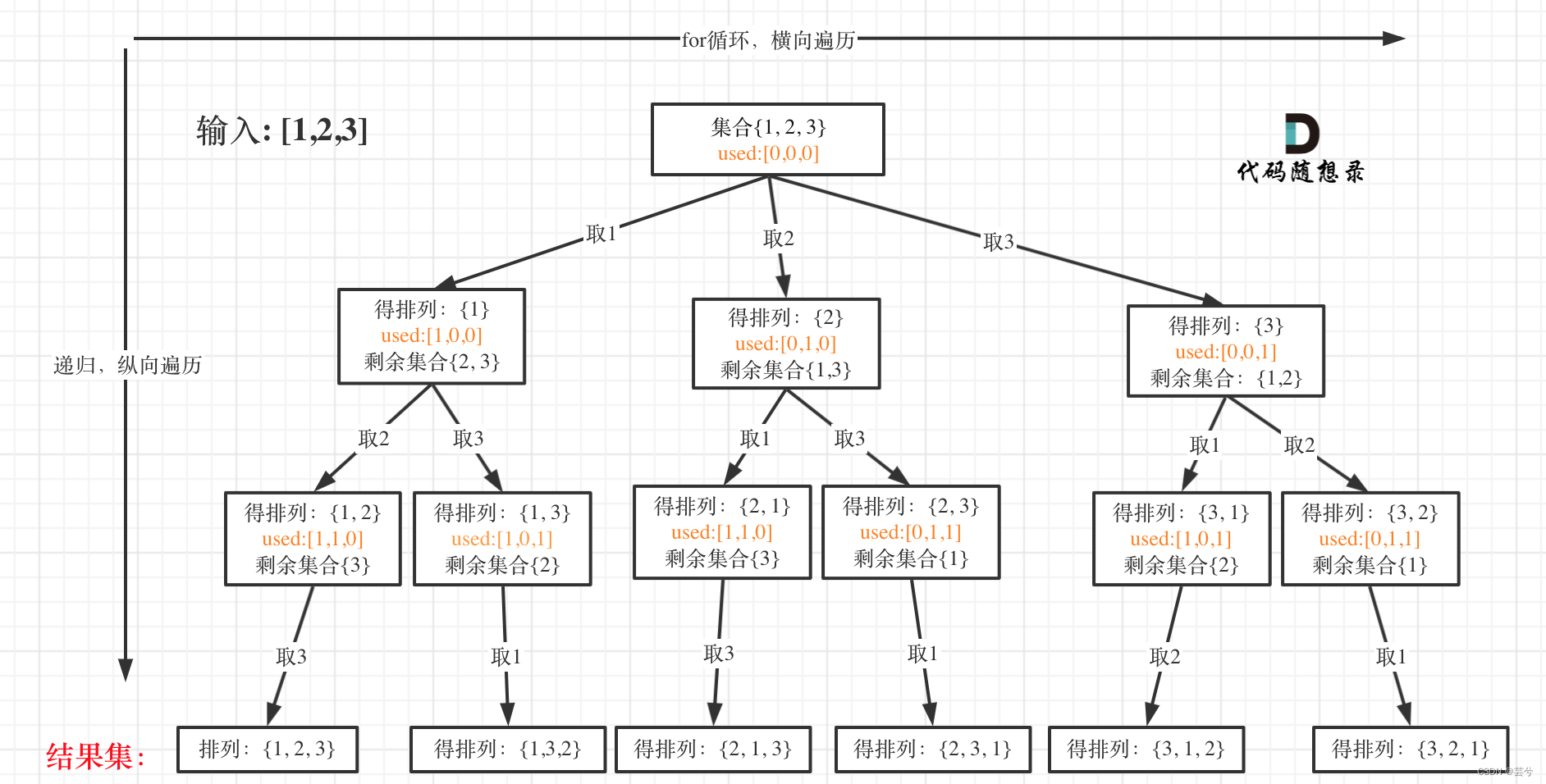
排列与组合最大的不同在于，排列所得每个路径分支的长度是一致的，这是因为排列是有序的，每个位置除了已经选择过的元素，都可以作为选择也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。因此排列问题不再需要start来限制元素选择范围，因为凡是之前没有选择的元素，都可以选择。

全排列通用解题技巧

终止条件：
每个排列的长度与原始数组num长度一致，因此当path分支深度达到num.size()时终止递归。

每层遍历：

排列问题通用的做法是，每次都从num数组的头遍历到尾，但是利用一个与num数组等大小的used数组，每次path填入元素num[i]后，将used[i]标记为已使用， used数组一般设置为bool类型:

vector<bool> used(nums.size(), false);

class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking (vector<int>& nums, vector<bool>& used) {// 此时说明找到了一组if (path.size() == nums.size()) {result.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {if (used[i] == true) continue; // path里已经收录的元素，直接跳过used[i] = true;path.push_back(nums[i]);backtracking(nums, used);path.pop_back();used[i] = false;}}vector<vector<int>> permute(vector<int>& nums) {result.clear();path.clear();vector<bool> used(nums.size(), false);backtracking(nums, used);return result;}
};

注：回溯时，除了path撤销，used数组同样需要撤销。
组合、子集问题从i = start开始遍历
排列问题从i = 0开始遍历

交换法实现全排列

既然每个排列最终长度与num保持一致，那么其实path可以不必从0开始一个个构建，而是可以直接由num换序得到。

考虑排序的规则：
定义递归：
index表示最终排列排到第index个数，这个数可以排index右边所有的数，因此可以用交换的方式，index右边所有的元素交换到该位置，回溯撤销时再交换一遍，换回去即可。

    vector<vector<int>> permute(vector<int>& nums) {auto ans = vector<vector<int>>();permutationBack(0, ans, nums);return ans;}void permutationBack(int index, vector<vector<int>> &ans, vector<int> &path) {if (index == path.size()) {ans.emplace_back(path);return;}for (int i = index; i < path.size(); i++){swap(path[i], path[index]);permutationBack(index + 1, ans, path);swap(path[i], path[index]);}}

排列去重

47.全排列 II
给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。
示例 1：
输入：nums = [1,1,2]
输出： [[1,1,2], [1,2,1], [2,1,1]]

排列本身需要used数组记录已经排过的元素，排列不像子序列那样需保证相对顺序，因此子集和组合中使用的两种去重方法，每层使用set去重和排序后把重复元素堆一块儿再去重的技巧都是可行的。
由于使用set比较慢，这里给出排序后堆一块再去重的解法：
先把重复的堆一块，在利用used数组判断重复的是上下层之间还是当前层内，因为当前层内used都是false，而上下层间，上层的used置为true。故可以利用这个进行层内的去重。

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking (vector<int>& nums, vector<bool>& used) {// 此时说明找到了一组if (path.size() == nums.size()) {result.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {// used[i - 1] == true，说明同一树枝nums[i - 1]使用过// used[i - 1] == false，说明同一树层nums[i - 1]使用过// 如果同一树层nums[i - 1]使用过则直接跳过if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}if (used[i] == false) {used[i] = true;path.push_back(nums[i]);backtracking(nums, used);path.pop_back();used[i] = false;}}}
public:vector<vector<int>> permuteUnique(vector<int>& nums) {result.clear();path.clear();sort(nums.begin(), nums.end()); // 排序vector<bool> used(nums.size(), false);backtracking(nums, used);return result;}
};

分割问题

LeetCode131.分割回文串
给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例: 输入: “aab” 输出: [ [“aa”,“b”], [“a”,“a”,“b”] ]
分割问题实际上是分割线位置的组合问题

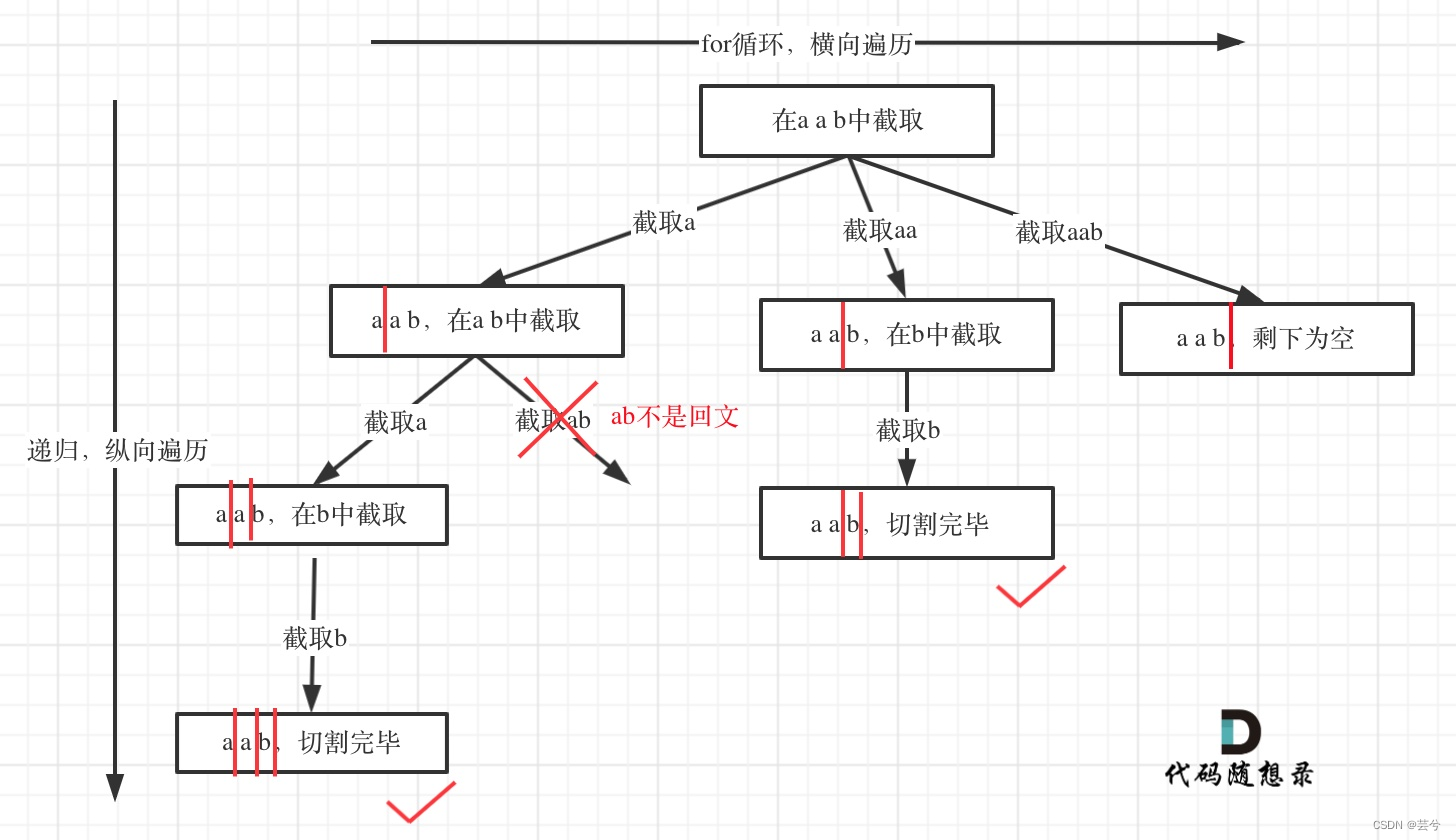
判断是否为回文字符串：
左右双指针法：

bool isPalindrome(string s) {int left = 0, right = s.length()-1;while ( left <= right){if (s[left] != s[right]) {return false;}left++;right--;}return true;
}

明确分割问题为分割线位置组合后，那么解法与组合问题是一致的。
for循环从i = start开始遍历，到s.length结束，终止条件为start到了原始字符串末尾。
每次切割下start到i之间的部分：
string tmp = s.substr(start, i - start + 1);
递归更新时，下一个start位置为分割线i位置的下一个:
partBacktracking(i + 1, ans, path, s)
如果分割出的是回文则继续递归，否则跳过。

void partBacktracking(int start, vector<vector<string>> &ans, vector<string> &path, string &s) {if (start == s.length()) {ans.emplace_back(path);return;}for (int i = start; i < s.length(); i++){string tmp = s.substr(start, i - start + 1);  if (isPalindrome(tmp)) {path.emplace_back(tmp);partBacktracking(i + 1, ans, path, s);path.pop_back();}else{continue;}}
}vector<vector<string>> partition(string s) {vector<string> path;vector<vector<string>> ans;partBacktracking(0, ans, path, s);return ans;
}

注：涉及到区间段和区间段长度，一定要明确区间开闭情况，例如我这里字符串截取是左右都是闭区间，左边是start，右边是i，闭区间，长度为 i - start + 1.

另外由于是闭区间，所以更新时，新的左边界为原来的右边界加1，即下一层的start变为了 i + 1