『牛角书』鸿蒙小游戏

黑白棋游戏

实现过程

一、绘制棋盘

首先我们使用css绘制棋盘，绘制一个14*14的正方形格子棋盘，但是需要注意，因为我们落子是落在四个格子之间的交界点上的，而不是落在格子里的，所以怎办呢？我们可以先绘制一个15*15的辅助正方形格子，然后再在其中间绘制一个14*14,这样落棋在15*15的格子里，而在14*14的格子里就可以看到落棋是在交界点里。

首先绘制一个15*15的正方形格子。

2. 然后再在其中间绘制一个14*14的正方形格子，这样的话，棋子就绘制在15*15的格子里，而在 14*14的棋盘里就显示是在格子交界点上了。

最后把15*15的边距去掉，就得到一个正常的14*14的棋盘了，怎样是不是很漂亮。

其实不需要这么麻烦的，直接绘制一个14*14的格子就可以了，可以使用css的::before和::after选择器来绘制格子线条。一开始也想用这么这样处理的，但是发现好像还没集成这两个选择器进来

二、实现落棋功能

首先在data声明一个arr为15*15的空数组，也就是长度为225的空数组。数组值只能更新为：

1：存放黑棋
-1：存放白棋

在标签里定义两个class来绘制黑棋和白棋

<divclass="li{{item == '1' ? 'black' : ''}} {{item == '-1' ? 'white': ''}}"for="{{(index,item) in arr}}"tid="item"οnclick="play(index)"
></div>

在点击play落棋时，传入当前落棋的位置

play(e){// 针对数组内的数据修改，请使用splice方法生效数据绑定变更this.arr.splice(e,1,'1'); 
}

上面代码传入1，则点击显示黑棋

到这里还不行，需要做交换走棋，黑棋走完，到白棋走，并且走过的位置不允许再走棋。

在data定义holder为当前持棋者：

1：存放黑棋，默认持黑棋先走
-1：存放白棋

play(e){if(this.arr[e] == '1' || this.arr[e] == '-1'){console.log('该处已经有棋了');return false;}// 针对数组内的数据修改，请使用splice方法生效数据绑定变更this.arr.splice(e,1,this.holder);// 交换走棋this.holder = this.holder == '1' ? '-1' : '1';},

三、计算赢棋方式

我们都知道要赢棋就得同色5颗棋子连成一条线，包括横向，竖向，斜向，斜向左边和斜向右边四种方式。那么我们就要把这几种方式拆分出来一一计算统计。

通过上面的序号，我们不难发现几个规律。

#### 1. 横向赢棋方式

横向赢棋方式是五个棋子每两两相差一个数值，所以每相邻棋子就是一个+1和-1的过程。

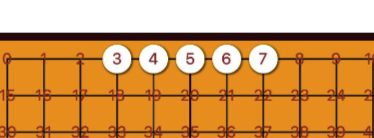
2. 竖向赢棋方式

竖向赢棋方式上下连成一排，我们知道一行只有15个格子，每个棋子都相差15数值，所以每相邻棋子之间都是+15和-15的过程。

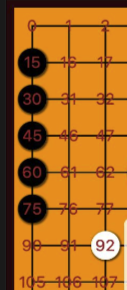
3. 左斜向赢棋

左斜方向通过观察不难发现每两两棋子之间相差+14和-14。

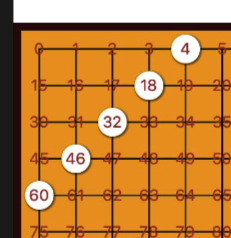
4. 右斜向赢棋

右边斜方向也可以看出每相邻棋子之间相差+16和16。

四、实现赢棋计算

通过上面一比较，是不是瞬间就觉得其实没那么难了呢，我们只要计算好每次落棋的序号和之前落棋的序号进行一对比，只要满足条件的五个棋子，就赢棋了。

实现思路： 以黑棋、横向为例子，通过递归算法，通过计算+1 || -1是否都有黑棋的记录，有则记录累计一次，每次计算完成，则去判断当前累计次数是否等于5，如果不是，则还没有赢，如果为5次，则说明赢棋了。

下面是实现代码：

//id: 当前棋子的序号 d: 计算方式，比如横向是 +1 和 -1，arr是累计下来的序号结果。 
compute(id,d,arr){id = parseInt(id);if(this.arr[id + d] && this.arr[id + d] == this.holder){arr.push(id);this.compute(id + d, d, arr);} else{arr.push(id);}},

下面代码是判断是否赢棋的方法

// 判断是否赢了
getResult(arr){if(arr.length > 5){console.log(this.holder + '赢棋'); //this.holder是定义的当前下棋的一方// 累计清0arr.length = 0;} else {// 累计清0arr.length = 0;}
},

我们在每次点击下棋的时候，都调用一次统计累计次数方法和计算赢棋的方法。

// 横向赢方法
this.compute(e, 1, this.arr1); //arr1是定义好的累计次数多数组
this.compute(e, -1, this.arr1);
this.getResult(this.arr1);

结合上面计算方式，我们其他的赢棋方式一样可以这样统计来计算。

// 点击下棋方法
play(e){if(this.isEnd) return;if(this.arr[e] == '1' || this.arr[e] == '-1'){console.log('该处已经有棋了');return false;}// 针对数组内的数据修改，请使用splice方法生效数据绑定变更this.arr.splice(e,1,this.holder);// 横向赢方法this.compute(e, 1, this.arr1);this.compute(e, -1, this.arr1);this.getResult(this.arr1);// 竖向赢方法this.compute(e, 15, this.arr1);this.compute(e, -15, this.arr1);this.getResult(this.arr1);//右斜赢方法this.compute(e, 14, this.arr1);this.compute(e, -14, this.arr1);this.getResult(this.arr1);// 左斜赢方法this.compute(e, 16, this.arr1);this.compute(e, -16, this.arr1);this.getResult(this.arr1);//    交换走棋this.holder = this.holder == '1' ? '-1' : '1';

下面看看效果。

到这里结束了吗？不，还没结束，这里还存在一些bug问题，比如说我们横向的时候是通过计算两棋子之间是否存在+1和-1的关系，但是如果两个棋子是14，15呢？这时候是已经换行了，显然是不能成立的，但是计算结果这种方式是成立的。所以我们要解决掉这个问题，包括斜向。

五、优化计算方法

其实无非两种结果，一种就是换行了，+1的时候换行到第一列数值了，-1的时候换行到最后一列数值了，那么我们把第一列和最后一列单独拉出来，进行比较，

是否在+1、-14，+16的数值是否在第一列存在，如果存在就不进行累计。
是否在-1、+14、-16的数值是否在最后一列存在，如果存在就不进行累计。
这里为什么没有+15和-15呢，因为竖向不存在这个问题。

下面我们来用代码实现。

// id: 为原id+d, d: 为计算方式。
scree(id,d){if((d == 1 && this.colOne.indexOf(id) > -1)|| (d == -1 && this.colEnd.indexOf(id) > -1)|| (d == 14 && this.colEnd.indexOf(id) > -1)|| (d == -14 && this.colOne.indexOf(id) > -1)|| (d == 16 && this.colOne.indexOf(id) > -1)|| (d == -16 && this.colEnd.indexOf(id) > -1)){return false;}return true;
},

最后，我们在计算判断的时候加上这个判断条件即可 this.scree(id+d,d)

compute(id,d,arr){id = parseInt(id);if(this.arr[id + d] && this.arr[id + d] == this.holder && this.scree(id+d,d)){arr.push(id);this.compute(id + d, d, arr);} else{arr.push(id);}
},

最后，我们来看看最终的效果

总结

该方法是使用div+css+js实现的双人对战游戏，在使用css的时候发现相比web端的属性，还是少了很多，比如绘制棋盘的时候想用::before和::after选择器来绘制，但是发现当前还没有这个属性，还有想绘制一个好看有弧度高光的棋子，想使用内阴影实现，但是目前也还并不支持内阴影。不过相信后续会更新，这样web前端开发上手HarmonyOS JSAPI就容易多了。