本节大纲内容

考试要求

1. 理解导数和微分的概念，理解导数与微分的关系，理解导数的几何意义.
2. 会求平面曲线的切线方程和法线方程，了解导数的物理意义.
3. 会用导数描述一些物理量，理解函数的可导性与连续性之间的关系.
4. 掌握导数的四则运算法则和复合函数的求导法则，掌握基本初等函数的导数公式.
5. 了解微分的四则运算法则和一阶微分形式的不变性，会求函数的微分.
6. 了解高阶导数的概念，会求简单函数的高阶导数.
7. 会求分段函数的导数，会求隐函数和由参数方程所确定的函数以及反函数的导数.
8. 理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理.
9. 了解并会用柯西(Cauchy)中值定理.
10. 掌握用洛必达法则求未定式极限的方法.
11. 理解函数的极值概念，掌握用导数判断函数的单调性和求函数极值的方法.
12. 掌握函数最大值和最小值的求法及其应用.
13. 会用导数判断函数图形的凹凸性，会求函数图形的拐点以及水平、铅直和斜渐近线，会描绘函数的图形.
14. 了解曲率、曲率圆与曲率半径的概念，会计算曲率和曲率半径.

考试内容

• 导数和微分的概念

• 导数的几何意义与物理意义

	另外还有切线方程和法线方程。物理上可以理解为瞬时速度。

• 函数的可导性与连续性的关系

• 平面曲线的切线和法线

• 导数和微分的四则运算

• 基本初等函数的导数

• 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法

• 高阶导数

• 一阶微分形式的不变性

• 微分中值定理

   中值定理的理解并不难，难点在于如何运用。注意多训练有关中值定理的题目，得以灵活运用。
  

• 洛必达法则

• 函数单调性的判别

• 函数的极值

• 函数图形的凹凸性、拐点及渐近线

• 函数图形的描绘

• 函数的最大值与最小值

   在函数驻点和导数不存在的点中，函数值最大的为最大值，最小的为最小值。
  

• 弧微分

• 曲率的概念

• 曲率圆与曲率半径

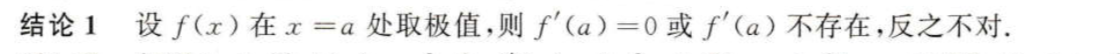
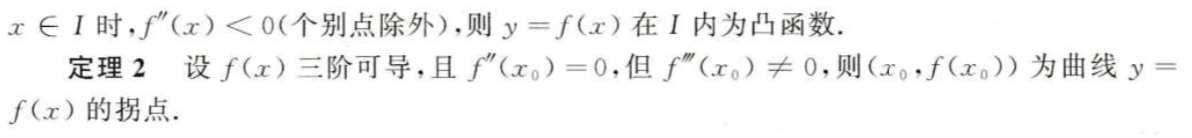
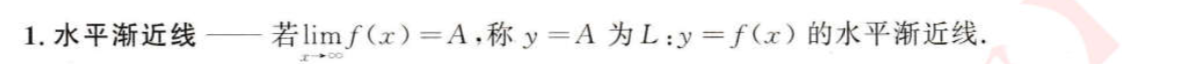
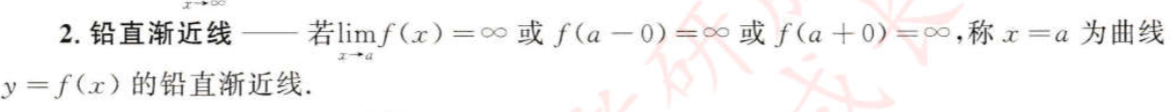
	推导过程可以只做了解，不必记忆