题目：压缩感知应用——单像素相机

============================================================

参考文献：

1）Rachel Zhang的专栏，压缩感知进阶——有关稀疏矩阵：http://blog.csdn.net/abcjennifer/article/details/7748833

2）白凌云，梁志毅，徐志军. 基于压缩感知理论的单像素成像系统研究. 计算机工程与应用，2011，47(33)：116-119.

3）陈 涛，李正炜，王建立，王 斌，郭 爽. 应用压缩传感理论的单像素相机成像系统. 光学精密工程，2012，20(11)：2523-2530.

============================================================

一、单像素相机介绍

学习研究压缩感知理论，肯定得听说rice大学的单像素相机，而理解一个典型压缩感知系统的组成，从单像素相机入手也不失为一种选择，所以我也学习一下。

过多的文字叙述不再重复，直接从三个参考文献中选取一些有代表性的文字及图片即可：

文献2：

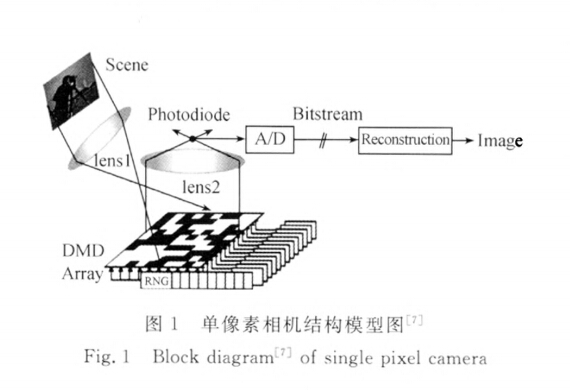
文献3：

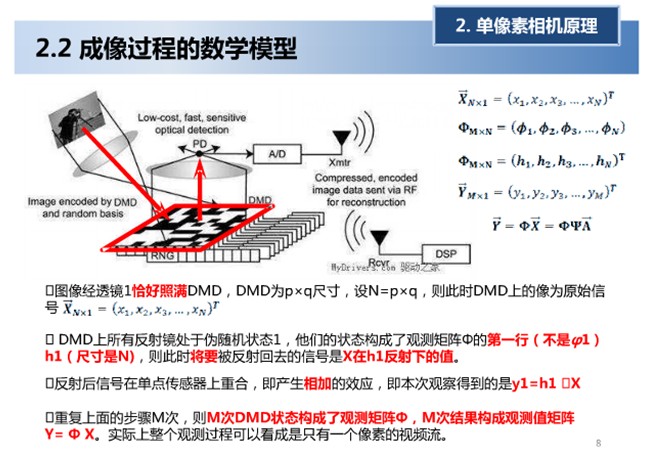
文献1：（个人感觉两张很经典的图片）

看了文献2和文献3两部分后基本就会对单像素相机的原理有所了解了，而文献1的两张图片尤其是第二张（2.2成像过程的数学模型）描述最为清晰。

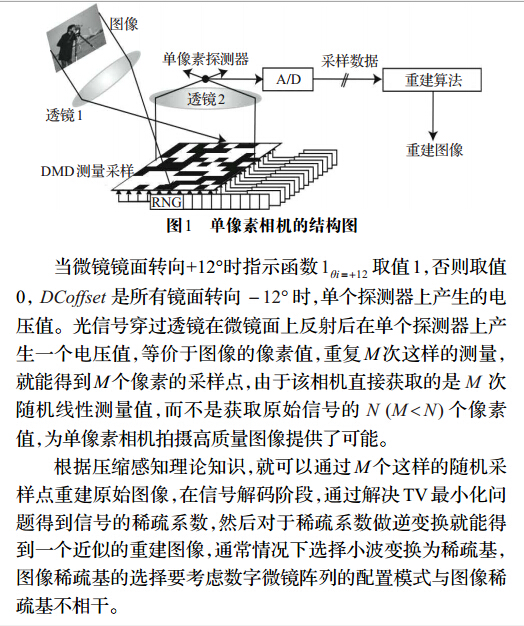
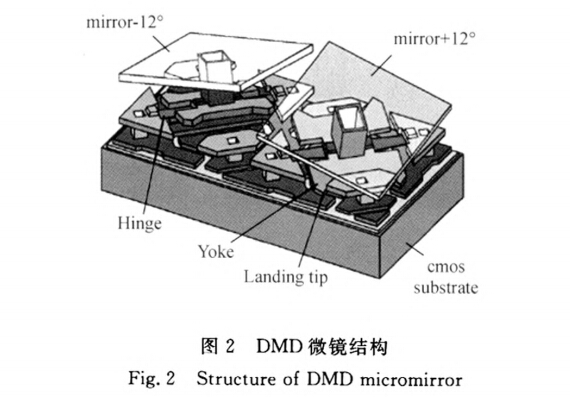
当图片经过透镜1恰好照满到DMD上时，其中DMD由N个如文献3图2（包括两个）中的微镜结构，相当于将图片转换成一个N维信号X，我们要对信号通过Φ进行一个压缩观测，由N维的信号X得到一个M维的观测信号Y，我们是通过操纵DMD共M次得到M个值，DMD的M次状态分别构成Φ的M行，通过M次观测即完成Y=ΦX整个过程。

单像素相机的基本原理就是这么简单，至于内部深层次的理论问题比如Φ是否满足RIP性质等等可以去看看参考文献2和文献3.

============================================================

二、几个问题

在这里我有几个问题：

1、几乎所有的压缩感知文献中都会提到压缩感知是突破Nquist采样定理的限制，单像素相机里不需要考虑采样定理么？

2、压缩感知理论基于信号可以稀疏表示，在文献中一般都会说信号X可以在稀疏基Ψ中稀疏表示，而单像素相机中的Ψ体现在哪里？

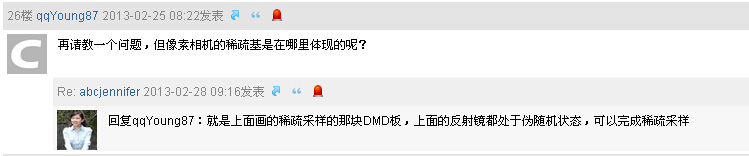
在文献1的评论里也有网友提出了这个问题：

3、我们在压缩感知的文献中信号X都是做为离散信号处理的，Y=ΦX完成压缩采样，如果是模拟信号怎么办呢？

【jbb0523博主的理解】

1、个人感觉，这里我们忽略了一点，我们现在面对的信号是一幅静止的图片，你的M次观测花多长时间，而对的始终是这幅图片（是不是可以这样理解，不管你观测还是不观测，图片就在那里，不增不减），所以你可以从容的完成对图片的M次观测（或者可以理解成采样），但如果这里不是一幅静态的图片而是一个视频呢？你是不是就要考虑对视频的每一帧要完成M次采样，所以要在每一帧图像变化前（设每一帧持续时间为T）完成这M次采样，这是不是也算是采样率的概念呢？即在时间T内完成M次观测（或者说是采M个点，当然这个采样和普通意义上的采样并不一样），不知道个人的理解是否偏离有单像素相机的出发点，个人感觉你用相机拍照时景色也并不是静止的啊。

参考文献1 的评论中第23楼网友horrorfrog 提到“cs没有否定奈奎斯特采样定理，只不过cs是以信号的稀疏性为先验知识，奈奎斯特采样定理是以信号带宽为先验知识。”

2、博主Rachel Zhang(abcjennifer)在对26楼的回复中说“反射镜处于伪随机状态，可以完成稀疏采样”，这里反射镜处于伪随机状态等价来说就是Φ是一个伪随机矩阵，根据压缩感知的相关知识我们知道，稀疏基Ψ要与观测矩阵Φ不相关，所以观测矩阵Φ我们经常采样高斯随机矩阵来担当（比如在Rachel Zhang的压缩感知Helloworld程序中就是令观测矩阵Phi=randn(M,N);，这是一个M*N的一个高斯白噪声矩阵，即高斯随机矩阵吧），那么稀疏基Ψ在哪里呢？这个在实际中我们认为信号X可以在稀疏基Ψ上稀疏表示，当然对于不同种类的信号，能最稀疏表示它的稀疏基Ψ是不同的，例如在Rachel Zhang的压缩感知Helloworld程序稀疏基是用傅里叶变换基（Psi=fft(eye(N,N))/sqrt(N);），而在看过的一篇文献（张颖超，茅丹，胡凯. 压缩传感理论在心电图信号恢复问题上的研究. 计算机研究发展，2014，51(5)：1018-1027）中就是在研究不同类别的心电信号在不同小波基上稀疏表示的情况，比较恢复的效果。
也就是说在单像素相机中，我们已为图片找好了稀疏基Ψ，然后在观测时保证观测矩阵Φ与稀疏基Ψ不相关即可。在这个系统里没有直观的体现出稀疏基Ψ，但在恢复算法里会使用稀疏基Ψ，当然你可以尝试不同的稀疏基Ψ去观查哪一个稀疏基的效果更好，不同的信号最合适的稀疏基Ψ也是不同的。
3、其实单相素像机中的图片就是一个模拟信号，只是经过DMD把它分成了N个值即N维信号X，然后Y=ΦX完成压缩观测得到M维信号Y（得到的值还是一个模拟值，不过这里的模拟值就是另一个概念了，即Y中的每一个元素值）。这里深究的话应该就是AIC（Analog to Information Converter，模拟信息采样）的概念了吧（具体AIC怎么实现还没有细看，今天下载了六七篇文献打算在未来几天看一下，单像素相机中由实际的图片得到M维的观测值Y是不是一个AIC的概念呢？），如果非要AD采样得到N维的信号X再压缩观测得到M维的Y意义何在呢？相当于说高成本的ADC已经使用，然后在接收端还得经过复杂的重建算法，好折腾的感觉，这和压缩感知的初衷就背离了吧，好多文献中都会说普通的压缩系统是先采样再压缩，而压缩感知是边采样边压缩………


以上就是个人的几点理解，后续有了深入的理解再发文，争取未来几天弄懂AIC的基本原理……

感慨：在沙威大牛的“压缩传感”引论中提到，他用了一周的时间阅读文献、思考问题、编程序、直到写出“压缩传感”引论，真心感觉人和人之间的差别怎么就那么大呢？我都看了好几个一周了，单单消化Rachel Zhang(abcjennifer)引用其程序作为Helloworld那篇博文就不止花了一个星期而且感觉还没消化彻底，哎，只能多多努力了，应该是要更加更加的努力……