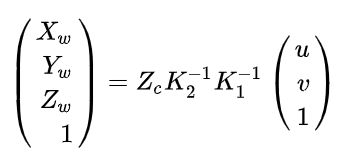像素坐标系、图像坐标系、相机坐标系、世界坐标系

上周发现对这四个坐标系之间的转换没有一个清晰的概念，这个下午写第一篇博客重新学习记录一下。

图片来源：《视觉SLAM十四讲》第二版P91

---

1、图像坐标系$\to$​像素坐标系

像素坐标系通常的定义方式是：原点$o{}^{\prime }$位于图像的左上角，$u$轴向右与$x$轴平行，$v$轴向下与$y$轴平行。

图像坐标系在这里指的是成像平面坐标系，在《视觉SLAM十四讲》中像素坐标系和图像坐标系是一样的（第一版 P72）。

像素坐标系与图像坐标系之间相差了一个缩放和平移，由此图像坐标系$P{}^{\prime }$的坐标$[X{}^{\prime },Y{}^{\prime }]$与像素坐标$[u,v]$的关系为：
$$\{\begin{array}{l}u=\alpha X^{\prime }+c_x\\ v=\beta Y^{\prime }+c_y\end{array}$$

---

2、图像坐标系$\to$​相机坐标系

由于三角形相似关系有（去掉负号）：
$$\frac{Z}{f}=\frac{X}{X^{\prime }}=\frac{Y}{Y^{\prime }}$$
所以式(1)变为：
$$\{\begin{array}{l}u=f_x\frac{X}{Z}+c_x\\ v=f_y\frac{Y}{Z}+c_y\end{array}$$
转换为矩阵形式为：
$$\left(\begin{array}{l}u\\ v\\ 1\end{array}\right)=\frac{1}{Z}\left(\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{l}X\\ Y\\ Z\end{array}\right)\triangleq \frac{1}{\mathbf{Z}}\mathbf{KP}$$

$$Z\left(\begin{array}{l}u\\ v\\ 1\end{array}\right)=\left(\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{l}X\\ Y\\ Z\end{array}\right)\triangleq \mathbf{KP}$$

其中，$K$为内参数矩阵（Camera Intrinsics）。

---

3、相机坐标系$\to$​世界坐标系

在齐次坐标下，相机坐标和世界坐标的关系为
$$p_c=T_{cw}{p}_w=T_{wc}^{-1}{p}_w$$
在非齐次坐标下，相机坐标和世界坐标的关系为
$$P_c=R{P}_w+t$$
其中，相机的位姿$R，t$称为相机的外参数矩阵（Camera Extrinsics）。

所以式(4)转化为
$$Z{P}_{uv}=Z\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]\triangleq \mathbf{KP}=\mathbf{K}(\mathbf{R}{\mathbf{P}}_{\mathbf{w}}+\mathbf{t})=\mathbf{KT}{\mathbf{P}}_{\mathbf{w}}$$
注意最后一个式子隐含了一次其次坐标到非齐次坐标的转换。

---

总结

最后简单归纳关系图如下：

单目相机的成像过程（P90）：

---

References

像素坐标系与图像坐标系_在路上DI蜗牛的博客-CSDN博客_图像坐标系

世界坐标系，相机坐标系，图像坐标系，像素坐标系的转换 - 知乎 (zhihu.com)