定义

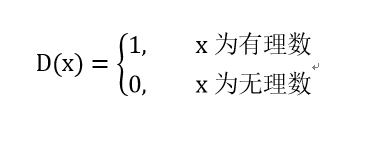
性质

狄利克雷函数是一个有界的偶函数，且任何有理数都是它的周期，它没有最小的周期

 

应用

函数 f(x) 在点 x=x0 可导，那么 f(x) 在点 x=x0 处必然连续，如果函数 f(x) 在点 x=x0 处可导，并不一定存在点 x=x0 的某个邻域，使得函数在这个邻域内连续

使用狄利克雷函数构造一个反例

根据 ”无穷小量乘有界函数仍然是无穷小量“ 可知上述结果为 0 ， 故 f(x) 在点 x=x0 处连续。

但是在 x=0 的任何一个邻域内，都有无数个有理数，也有无数个无理数，于是就会出现这样一个现象：不管多小的一个区间内，跳跃间断点多到我们数不过来，除了 x=0 点外，处处间断

根据 ”无穷小量乘有界函数仍然是无穷小量“ 可知上述结果为 0 ， 故 f(x) 在点 x=x0 处可导。

故，f(x) 除了在点 x=x0 处可导、在点 x=x0 处连续外，在 x=0 的任何一个邻域内都不连续