1. 2105 IP Address

描述
Suppose you are reading byte streams from any device, representing IP addresses. Your task is to convert a 32 characters long sequence of ‘1s’ and ‘0s’ (bits) to a dotted decimal format. A dotted decimal format for an IP address is form by grouping 8 bits at a time and converting the binary representation to decimal representation. Any 8 bits is a valid part of an IP address. To convert binary numbers to decimal numbers remember that both are positional numerical systems, where the first 8 positions of the binary systems are:

输入
The input will have a number N (1<=N<=9) in its first line representing the number of streams to convert. N lines will follow.
输出
The output must have N lines with a doted decimal IP address. A dotted decimal IP address is formed by grouping 8 bit at the time and converting the binary representation to decimal representation.
样例输入
4
00000000000000000000000000000000
00000011100000001111111111111111
11001011100001001110010110000000
01010000000100000000000000000001
样例输出
0.0.0.0
3.128.255.255
203.132.229.128
80.16.0.1

#include<iostream>
#include<cstring>
#include<string>
using namespace std;int main() {int m;string s;cin >> m;while(m--){int a[4];cin >> s;int ans = 0, pow = 1;for (int i = 31; i >= 0; i--) {ans += (s[i] - '0')*pow;pow *= 2;if(i%8==0) //每8个数一组 {a[i / 8] = ans;ans = 0;pow = 1;} }cout << a[0] << '.' << a[1] << '.' << a[2] << '.' << a[3] << endl;}
}

2. 2181 Jumping Cows

描述
Farmer John’s cows would like to jump over the moon, just like the cows in their favorite nursery rhyme. Unfortunately, cows can not jump.

The local witch doctor has mixed up P (1 <= P <= 150,000) potions to aid the cows in their quest to jump. These potions must be administered exactly in the order they were created, though some may be skipped.

Each potion has a ‘strength’ (1 <= strength <= 500) that enhances the cows’ jumping ability. Taking a potion during an odd time step increases the cows’ jump; taking a potion during an even time step decreases the jump. Before taking any potions the cows’ jumping ability is, of course, 0.

No potion can be taken twice, and once the cow has begun taking potions, one potion must be taken during each time step, starting at time 1. One or more potions may be skipped in each turn.

Determine which potions to take to get the highest jump.
输入
Line 1: A single integer, P
Lines 2…P+1: Each line contains a single integer that is the strength of a potion. Line 2 gives the strength of the first potion; line 3 gives the strength of the second potion; and so on.
输出
Line 1: A single integer that is the maximum possible jump.
样例输入
8
7
2
1
8
4
3
5
6
样例输出
17

一、题意

概括题意：给定一串有n个数的串，要求找出一个子串，在子串的奇数位置+，在子串的偶数位置-。

二、算法

本题可采用贪心算法，贪心代码的简易程度取决于你对这题的抽象程度，以下给出一个抽象程度最高的解法。

抽象解释：

首先建立坐标系，画出数据点，并用曲线相连，如下：

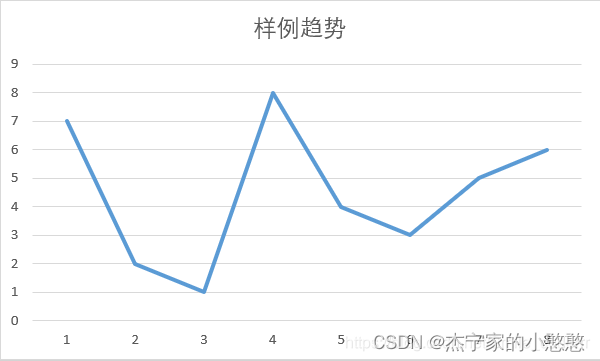
而贪心总体想在+的时候多+一点，在-的时候多减一点，那么我们则可以使每次+的时候都在曲线的波峰（即最近的最高值），每次-的时候在曲线的波谷（即最近的最小值）。

则算法步骤如下：初始为奇数次

若为奇数次：从当前的数开始进行前后比较，若前一个数比后一个数大，则+上这个数，设此时为偶数次，跳转到偶数次

若为偶数次：从当前的数开始进行前后比较，若前一个数比后一个数小，则-上这个数，设此时为奇数次，跳转到奇数次

#include <iostream>
using namespace std;bool odd_even = true;
int a[150002];
int sum = 0;
int main (){int n;cin>>n;for(int i = 0; i < n; i++){cin>>a[i];}for(int i = 0; i < n; i++){if(odd_even == true){if(a[i] > a[i+1]){sum += a[i];	odd_even = false;}}else{if(a[i] < a[i+1]){sum -= a[i];odd_even = true;}}}cout<<sum<<endl;return 0;
} 

3. 2210 Metric Time

描述
The Metric Time is one of the most important points of PSOS Election Programme. The Time can be much easier calculated in operating systems. These systems are then more stable, which meets the main goal of the Party.

The length of one day is the same as with the “classic” time. The day is divided into 10 metric hours, each of them into 100 metric minutes, and each minute into 100 metric seconds. 10 metric days form one metric week, 10 metric weeks give one metric month, 10 metric months are called metric year. It is obvious this Metric Time is much better than the classic one.

Some opponent parties often complain that the Metric Time has also some drawbacks. First of all, it would be very difficult to change to the new time. PSOS Chairman decided to solve these problems all at once. He plans to publish a freeware utility which will be able to convert between the time formats. Your goal is to write one half of this utility, the program which converts classic time to Metric Time. Metric hours, metric minutes, and metric seconds are counted starting with zero, as usual. Metric days and metric months start with one. There exist metric year zero. The metric seconds should be rounded to the nearest smaller integer value. Assume that 0:0:0 1.1.2000 classic time is equal to 0:0:0 1.1.0 Metric Time.

Note that the classic year is leap, if it is an integer multiple of 4. The only exception are years divisible by 100 - they are leap only if they are an integer multiple of 400. For example, leap years are 1996, 2400, and 2000; leap years are not 1900, 2300, 2002.
输入
At the first line there is a positive integer N stating the number of assignments to follow. Each assignment consists of exactly one line in the form “hour:minute:second day.month.year” which is the date in the classic form (usual in most of European countries). The date is always valid, 2000 <= year <= 50000.
输出
The program must print exactly one line for each assignment. The line should have the form “mhour:mmin:msec mday.mmonth.myear” which is the Metric Time equal to the specified classic time.
样例输入
7
0:0:0 1.1.2000
10:10:10 1.3.2001
0:12:13 1.3.2400
23:59:59 31.12.2001
0:0:1 20.7.7478
0:20:20 21.7.7478
15:54:44 2.10.20749
样例输出
0:0:0 1.1.0
4:23:72 26.5.0
0:8:48 58.2.146
9:99:98 31.8.0
0:0:1 100.10.2000
0:14:12 1.1.2001
6:63:0 7.3.6848

#include<cstdio>
using namespace std;
int m[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};int main()
{int day,month,year,h,minu,sec,mday,mmonth,myear,mh,mminu,msec,days,y,secs,cas;
//    freopen("in.txt","r",stdin);scanf("%d",&cas);while(cas--){scanf("%d:%d:%d %d.%d.%d",&h,&minu,&sec,&day,&month,&year);days=0;for(y=2000;y<year;y+=4) //这里y不要每次加1不然会超时{if((y%100==0&&y%400==0)||(y%4==0&&y%100!=0))days+=1;}for(int i=1;i<month;i++)days+=m[i];if(month>2&&((year%100==0&&year%400==0)||(year%4==0&&year%100!=0)))days+=1;days+=(day-1);days+=(365*(year-2000));myear=days/1000;days%=1000;mmonth=days/100;days%=100;mday=days;secs=h*3600+minu*60+sec;secs*=125;secs/=108;mh=secs/10000;secs-=10000*mh;mminu=secs/100;secs-=100*mminu;msec=secs;printf("%d:%d:%d %d.%d.%d\n",mh,mminu,msec,mday+1,mmonth+1,myear);}return 0;
}

4. 2234 Matches Game

描述
Here is a simple game. In this game, there are several piles of matches and two players. The two player play in turn. In each turn, one can choose a pile and take away arbitrary number of matches from the pile (Of course the number of matches, which is taken away, cannot be zero and cannot be larger than the number of matches in the chosen pile). If after a player’s turn, there is no match left, the player is the winner. Suppose that the two players are all very clear. Your job is to tell whether the player who plays first can win the game or not.
输入
The input consists of several lines, and in each line there is a test case. At the beginning of a line, there is an integer M (1 <= M <=20), which is the number of piles. Then comes M positive integers, which are not larger than 10000000. These M integers represent the number of matches in each pile.
输出
For each test case, output “Yes” in a single line, if the player who play first will win, otherwise output “No”.
样例输入
2 45 45
3 3 6 9
样例输出
No
Yes

题意：有M堆火柴，没堆火柴个数不同。两个人轮流取火柴，可以拿少于该堆火柴数量的个数，一次拿一堆。求先手是否一定能赢

分析：好强大的推理！！

（1）只有一堆，先手赢
（2）两堆，一共2根火柴，后手赢 （取完一堆即可）
两堆，一共3根火柴，先手赢 （1+2格局，在2个的一堆中取1个，转化为前一种情形）
两堆，一堆2个，另一堆2个，后手赢 （取完一堆，或者取1个都必输）
两堆，一堆1个，另一堆3个，先手赢 （1+3格局，在3个的一堆中取2个，转化为2根的情形）
…
两堆，堆中火柴数目相等，后手赢
两堆，堆中火柴数目不等，先手赢
（3）三堆，一共3根火柴，先手赢
三堆，一共4根火柴，先手赢
三堆，一共5根火柴，1.1.3型先手赢 （因为总能够转化到两堆相等的情况）
三堆，一共5根火柴，2.2.1型先手赢 （因为总能够转化到两堆相等的情况）
三堆，一共6根火柴，2.2.2型先手赢
三堆，一共6根火柴，1.1.4型先手赢
三堆，一共6根火柴，1.2.3型后手赢
。。。。。。（此处省略高大上的证明部分）

结论：每一堆个数异或，如果等于0，后手赢，否则先手赢
结论：n 堆石子异或和不为 0 ，先手必胜，否则先手必输。

#include<iostream>
#include<cstdio>
using namespace std;
int a[100];
int main()
{int m;while(cin>>m){int i;for(i=0;i<m;i++) scanf("%d",&a[i]);int t=0;for(i=0;i<m;i++){t^=a[i];}if(t) printf("Yes\n");else printf("No\n");}return 0;
}

5. 2251 Dungeon Master

【熟悉不】
描述
You are trapped in a 3D dungeon and need to find the quickest way out! The dungeon is composed of unit cubes which may or may not be filled with rock. It takes one minute to move one unit north, south, east, west, up or down. You cannot move diagonally and the maze is surrounded by solid rock on all sides.

Is an escape possible? If yes, how long will it take?
输入
The input consists of a number of dungeons. Each dungeon description starts with a line containing three integers L, R and C (all limited to 30 in size).
L is the number of levels making up the dungeon.
R and C are the number of rows and columns making up the plan of each level.
Then there will follow L blocks of R lines each containing C characters. Each character describes one cell of the dungeon. A cell full of rock is indicated by a ‘#’ and empty cells are represented by a ‘.’. Your starting position is indicated by ‘S’ and the exit by the letter ‘E’. There’s a single blank line after each level. Input is terminated by three zeroes for L, R and C.
输出
Each maze generates one line of output. If it is possible to reach the exit, print a line of the form
Escaped in x minute(s).

where x is replaced by the shortest time it takes to escape.
If it is not possible to escape, print the line
Trapped!
样例输入
3 4 5
S…
.###.
.##…
###.#

##.##
##…

#.###
####E

1 3 3
S##
#E#

0 0 0
样例输出
Escaped in 11 minute(s).
Trapped!

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
using namespace std;
const int N=32;
int t[N][N][N],dx[6]={0,0,1,-1,0,0},dy[6]={1,-1,0,0,0,0},dz[6]={0,0,0,0,1,-1};
char s[N][N][N];
bool vis[N][N][N];
int nl,nr,nc,el,er,ec;
struct node{int l,r,c;
};
int bfs(int l,int r,int c)
{//多组输入，记得初始化数组 memset(t,0x3f,sizeof t);memset(vis,false,sizeof vis);t[l][r][c]=0;vis[l][r][c]=true;queue<node>q;q.push({l,r,c});while(q.size()){node temp=q.front();q.pop();if(temp.c==ec&&temp.l==el&&temp.r==er) break; for(int i=0;i<6;i++)//枚举下一步可以到达的6个位置 {int nz=temp.l+dz[i],nx=temp.r+dx[i],ny=temp.c+dy[i];if(nz>=1&&nz<=nl&&nx>=1&&nx<=nr&&ny>=1&&ny<=nc&&!vis[nz][nx][ny]&&s[nz][nx][ny]!='#')//判断位置是否走过以及是否合法 {vis[nz][nx][ny]=true;//标记为该位置已走过 t[nz][nx][ny]=t[temp.l][temp.r][temp.c]+1;//记录到达该位置的最短时间 q.push({nz,nx,ny});//将该位置入队 }}}return t[el][er][ec];
}
int main()
{while(1){scanf("%d%d%d",&nl,&nr,&nc);if(nl==0&&nr==0&&nc==0) break;int bl,br,bc;for(int i=1;i<=nl;i++)for(int j=1;j<=nr;j++)for(int k=1;k<=nc;k++){cin>>s[i][j][k];//因为有换行，读入一定要用cin if(s[i][j][k]=='S') bl=i,br=j,bc=k;//记录起点 if(s[i][j][k]=='E') el=i,er=j,ec=k;//记录终点 }int ans=bfs(bl,br,bc);if(ans!=0x3f3f3f3f) printf("Escaped in %d minute(s).\n",ans);else puts("Trapped!");}return 0;
} 

6. 2287 Tian Ji – The Horse Racing

描述
Here is a famous story in Chinese history.
That was about 2300 years ago. General Tian Ji was a high official in the country Qi. He likes to play horse racing with the king and others.

Both of Tian and the king have three horses in different classes, namely, regular, plus, and super. The rule is to have three rounds in a match; each of the horses must be used in one round. The winner of a single round takes two hundred silver dollars from the loser.

Being the most powerful man in the country, the king has so nice horses that in each class his horse is better than Tian’s. As a result, each time the king takes six hundred silver dollars from Tian.

Tian Ji was not happy about that, until he met Sun Bin, one of the most famous generals in Chinese history. Using a little trick due to Sun, Tian Ji brought home two hundred silver dollars and such a grace in the next match.

It was a rather simple trick. Using his regular class horse race against the super class from the king, they will certainly lose that round. But then his plus beat the king’s regular, and his super beat the king’s plus. What a simple trick. And how do you think of Tian Ji, the high ranked official in China?
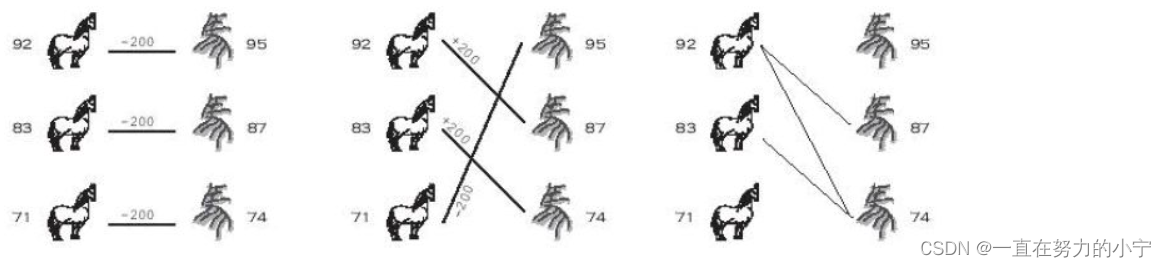Were Tian Ji lives in nowadays, he will certainly laugh at himself. Even more, were he sitting in the ACM contest right now, he may discover that the horse racing problem can be simply viewed as finding the maximum matching in a bipartite graph. Draw Tian’s horses on one side, and the king’s horses on the other. Whenever one of Tian’s horses can beat one from the king, we draw an edge between them, meaning we wish to establish this pair. Then, the problem of winning as many rounds as possible is just to find the maximum matching in this graph. If there are ties, the problem becomes more complicated, he needs to assign weights 0, 1, or -1 to all the possible edges, and find a maximum weighted perfect matching…

However, the horse racing problem is a very special case of bipartite matching. The graph is decided by the speed of the horses – a vertex of higher speed always beat a vertex of lower speed. In this case, the weighted bipartite matching algorithm is a too advanced tool to deal with the problem.

In this problem, you are asked to write a program to solve this special case of matching problem.
输入
The input consists of up to 50 test cases. Each case starts with a positive integer n ( n<=1000) on the first line, which is the number of horses on each side. The next n integers on the second line are the speeds of Tian’s horses. Then the next n integers on the third line are the speeds of the king’s horses. The input ends with a line that has a single `0’ after the last test case.
输出
For each input case, output a line containing a single number, which is the maximum money Tian Ji will get, in silver dollars.
样例输入
3
92 83 71
95 87 74
2
20 20
20 20
2
20 19
22 18
0
样例输出
200
0
0

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>#define ME0(x) memset(x,0,sizeof(x))
using namespace std;
int n;
int a[1005];
int b[1005];
int main()
{while(cin>>n,n){ME0(a);ME0(b);int sum=0;for(int i=0; i<n; i++)cin>>a[i];//田忌的马for(int i=0; i<n; i++)cin>> b[i];//齐王的马sort(a,a+n);//排序sort(b,b+n);int l1=0;int l2=0;int r1=n-1;int r2=n-1;while(l1<=r1){//田忌最快的马比齐王最快的马快，则两者比if(a[r1]>b[r2]){sum+=200;--r1;--r2;}//田忌最快的马比齐王最快的马慢，则用田忌最慢的马和齐王最快的马比if(a[r1]<b[r2]){sum-=200;++l1;--r2;}//速度相等if(a[r1]==b[r2]){//田忌最慢的马比齐王最慢的马快，则这两匹马比if(a[l1]>b[l2]){sum+=200;++l1;++l2;}//否则，用田忌最慢的马和齐王最快的马比else{if(a[l1]<b[r2])//田忌最慢的马比齐王最快的马快sum-=200;//加200++l1;//否则平局--r2;}}}cout<<sum<<endl;}
}

7. 2299 Ultra-QuickSort

描述
In this problem, you have to analyze a particular sorting algorithm. The algorithm processes a sequence of n distinct integers by swapping two adjacent sequence elements until the sequence is sorted in ascending order. For the input sequence
9 1 0 5 4 ,

Ultra-QuickSort produces the output
0 1 4 5 9 .

Your task is to determine how many swap operations Ultra-QuickSort needs to perform in order to sort a given input sequence.
输入
The input contains several test cases. Every test case begins with a line that contains a single integer n < 500,000 – the length of the input sequence. Each of the the following n lines contains a single integer 0 ≤ a[i] ≤ 999,999,999, the i-th input sequence element. Input is terminated by a sequence of length n = 0. This sequence must not be processed.
输出
For every input sequence, your program prints a single line containing an integer number op, the minimum number of swap operations necessary to sort the given input sequence.
样例输入
5
9
1
0
5
4
3
1
2
3
0
样例输出
6
0

题意是求归并排序时，至少要交换几次相邻的数字。
别人都说是求逆序对，规模这么大肯定不能暴力，这里还有个性质，要模拟一下归并排序，在归并排序的合并操作里，对于数列[l, mid] [mid + 1, r]的合并，i 从l开始循环，j从mid + 1开始循环，如果遇到a[i] > a[j] 则出现逆序，可以将a[j]放入辅助数组，同时j++，那么和a[j]逆序的数就有mid-i+1个，因为序列是有序的[i, mid]的所有的数都是大于a[j]的

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define N 500005using namespace std;typedef long long ll;int a[N], b[N], n;
ll ans; void Merge(int l1, int r1, int l2, int r2) 
{int cnt = 0;while (l1 <= r1 && l2 <= r2){if (a[l1] >= a[l2]) b[++cnt] = a[l2++], ans += r1 - l1 + 1;else b[++cnt] = a[l1++];}while (l1 <= r1) b[++cnt] = a[l1++];while (l2 <= r2) b[++cnt] = a[l2++];int j = r2;for (int i = cnt; i >= 1; i--) a[j--] = b[i];
}void Merge_sort(int l, int r)
{if (l >= r) return;{int mid = (l + r) >> 1;Merge_sort(l, mid);Merge_sort(mid + 1, r);Merge(l, mid, mid + 1, r); }
}
int main() 
{while (1){cin>>n;if(!n) break;ans = 0;for (int i = 1; i <= n; i++) scanf("%d", &a[i]);Merge_sort(1, n);printf("%lld\n", ans);}return 0;
}

8. 2349 Arctic Network

【最小生成树，看一遍代码不理解的话就算了】
描述
The Department of National Defence (DND) wishes to connect several northern outposts by a wireless network. Two different communication technologies are to be used in establishing the network: every outpost will have a radio transceiver and some outposts will in addition have a satellite channel.
Any two outposts with a satellite channel can communicate via the satellite, regardless of their location. Otherwise, two outposts can communicate by radio only if the distance between them does not exceed D, which depends of the power of the transceivers. Higher power yields higher D but costs more. Due to purchasing and maintenance considerations, the transceivers at the outposts must be identical; that is, the value of D is the same for every pair of outposts.

Your job is to determine the minimum D required for the transceivers. There must be at least one communication path (direct or indirect) between every pair of outposts.
输入
The first line of input contains N, the number of test cases. The first line of each test case contains 1 <= S <= 100, the number of satellite channels, and S < P <= 500, the number of outposts. P lines follow, giving the (x,y) coordinates of each outpost in km (coordinates are integers between 0 and 10,000).
输出
For each case, output should consist of a single line giving the minimum D required to connect the network. Output should be specified to 2 decimal points.
样例输入
1
2 4
0 100
0 300
0 600
150 750
样例输出
212.13

题意：输入S，N表示有N个哨所要通信，现在有S课卫星。然后输入N个点的坐标。有卫星的两个哨所之间可以任意通信（卫星是你分配的）；否则，一个哨所只能和距离它小于等于D的哨所通信。求D的最小值？

思路：其实就是求最小生成树，删掉S条边以后，最长的边的边权为多少？因为一定能形成最小生成树，所以我们在建立最小生成树的时候，本来需要建立N-1条边，那么现在只需要建立N-1-(S-1)条边即可。输出最后一条边的长度。

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int MAXN = 1005;
const int MAXM = 1005 * 1005;
int n, s, m, f[MAXN];
struct Point
{int x, y;
}point[MAXN];
struct Edge
{int u, v;double w;bool operator < (const Edge& A) const{return w < A.w;}
}edge[MAXM];
double dis(int a, int b)
{return sqrt(pow(point[a].x - point[b].x, 2) + pow(point[a].y - point[b].y, 2));
}
void init()
{for (int i = 0; i <= n; i++) f[i] = i;
}
int Find(int x){ return f[x] == x ? x : f[x] = Find(f[x]); }
double kruskal()
{init();sort(edge, edge + m);int cnt = 0;for (int i = 0; i < m; i++){int u = edge[i].u, v = edge[i].v;double w = edge[i].w;int root1 = Find(u), root2 = Find(v);if (root1 != root2){f[root1] = root2;cnt++;if (cnt == n - 1 - (s - 1)) return w;}}return -1.0;
}
int main()
{int T;scanf("%d", &T);while (T--){m = 0;scanf("%d%d", &s, &n);for (int i = 0; i < n; i++) scanf("%d%d", &point[i].x, &point[i].y);for (int i = 0; i < n; i++){for (int j = i + 1; j < n; j++){edge[m].u = i; edge[m].v = j; edge[m].w = dis(i, j);m++;}}printf("%.2f\n", kruskal());}return 0;
}
/*
1
2 4
0 100
0 300
0 600
150 750
*/

9. 2386 Lake Counting

描述
Due to recent rains, water has pooled in various places in Farmer John’s field, which is represented by a rectangle of N x M (1 <= N <= 100; 1 <= M <= 100) squares. Each square contains either water (‘W’) or dry land (‘.’). Farmer John would like to figure out how many ponds have formed in his field. A pond is a connected set of squares with water in them, where a square is considered adjacent to all eight of its neighbors.

Given a diagram of Farmer John’s field, determine how many ponds he has.
输入
Line 1: Two space-separated integers: N and M

Lines 2…N+1: M characters per line representing one row of Farmer John’s field. Each character is either ‘W’ or ‘.’. The characters do not have spaces between them.
输出
Line 1: The number of ponds in Farmer John’s field.
样例输入
10 12
W…WW.
.WWW…WWW
…WW…WW.
…WW.
…W…
…W…W…
.W.W…WW.
W.W.W…W.
.W.W…W.
…W…W.
样例输出
3
提示
OUTPUT DETAILS:

There are three ponds: one in the upper left, one in the lower left,and one along the right side.

这个题目是简单的深度搜索题目，题意：连天下雨，农夫的n*m田地里有积水，积水连成了小水洼，让你计算小水洼有几个。
易知，这个题目的做法是dfs，因为其“从某一个状态转移到另一个状态，直到其无法转移为止，且无固定初末状态”。

#include<iostream>
using namespace std;
int n,m;
char str[105][105];
void solve();
void dfs(int ,int );
int main()
{cin>>n>>m;//n行m列for(int i=0;i<n;i++)cin>>str[i];solve();return 0;
}
void solve()
{int res=0;for(int i=0;i<n;i++)for(int j=0;j<m;j++)if(str[i][j]=='W'){dfs(i,j);res++;}cout<<res<<endl;
}
void dfs(int x,int y)
{int nx,ny;str[x][y]='.';//走过的水坑更新为陆地//遍历上下左右八个方向for(int fx=-1;fx<=1;fx++)for(int fy=-1;fy<=1;fy++){nx=x+fx,ny=y+fy;//判断遍历的点是否在n*m的地盘内以及是否是水坑if(nx>=0&&nx<n&&ny>=0&&ny<m&&str[nx][ny]=='W')dfs(nx,ny);}}

10. 2388 寻找中位数

描述
在N（1<=N<10,000且N为奇数）个数中，找到中位数。
输入
第1行：N

第2至N+1行：每行是一个整数
输出
第一行：中位数
样例输入
5
2
4
1
3
5
样例输出
3

#include<cstdio>
#include<algorithm>
using namespace std;
int main()
{int i,l,t,d,m,n,x[26555];scanf("%d",&n);for(i=0;i<n;i++)scanf("%d",&x[i]);sort(x,x+n);m=(n+1)/2-1;printf("%d\n",x[m]);
}

11.2406 字符串乘方

【KMP算法也是看一遍能记住的话就打】
描述
给定两个字符串a和b,我们定义ab为他们的连接。例如，如果a=”abc” 而b=”def”， 则ab=”abcdef”。 如果我们将连接考虑成乘法，一个非负整数的乘方将用一种通常的方式定义：a^{0=””(空字符串)，a}(n+1)=a*(a^n)。

输入
每一个测试样例是一行可打印的字符作为输入，用s表示。s的长度至少为1，且不会超过一百万。最后的测试样例后面将是一个点号作为一行。
输出
对于每一个s，你应该打印最大的n，使得存在一个a，让s=a^n
样例输入
abcd
aaaa
ababab
.
样例输出
1
4
3

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#define N 1000000
using namespace std;
char c[N];
int Next[N];
int len;
void getnext()
{int i=0;int j=-1;Next[0]=-1;while(i<len)//多算一位{if(j==-1||c[i]==c[j]){i++;j++;Next[i]=j;}elsej=Next[j];}
}
int main()
{while(1){	cin>>c;if(strcmp(c,".")==0) break;len=strlen(c);getnext();if(len%(len-Next[len])==0)printf("%d\n",len/(len-Next[len]));elseprintf("1\n");}return 0;
}

12.2456 Aggressive cows

【牛栏问题 二分法 这个较简单】
描述
Farmer John has built a new long barn, with N (2 <= N <= 100,000) stalls. The stalls are located along a straight line at positions x1,…,xN (0 <= xi <= 1,000,000,000).

His C (2 <= C <= N) cows don’t like this barn layout and become aggressive towards each other once put into a stall. To prevent the cows from hurting each other, FJ want to assign the cows to the stalls, such that the minimum distance between any two of them is as large as possible. What is the largest minimum distance?
输入
Line 1: Two space-separated integers: N and C

Lines 2…N+1: Line i+1 contains an integer stall location, xi
输出
Line 1: One integer: the largest minimum distance
样例输入
5 3
1
2
8
4
9
样例输出
3
提示
OUTPUT DETAILS:

FJ can put his 3 cows in the stalls at positions 1, 4 and 8, resulting in a minimum distance of 3.

Huge input data,scanf is recommended.
题目大意：有c只牛，要把他们放在n个屋子里，每个屋子放一只牛，每个屋子都在一根数轴上，给出他们的坐标，要让每个屋子间的最小距离尽可能的大，问这个最大距离是多少

2<=c<=n<=1e5;0<=xi<=1e9

思路：先把坐标从小到大排序，然后二分查找这个最小距离，二分边界是从0，到最大坐标减最小坐标，每一次枚举，都从小到大遍历坐标，如果这个点减上一个点的距离小于mid，继续遍历下一个点，否则就把遍历到的点变成下一个点并统计合法点的数量，将合法点的数量与要求的点数进行对比

#include<iostream>
#include<algorithm>
#include<string.h>
#include<cstdio>
using namespace std;
int dis[100005];
int n, c;
bool check(int x)
{int cnt = 0;for (int i = 1, next = 2; i < n&&next<=n;){//i表示上一个点，next表示下一个点if (dis[next] - dis[i] < x){next++;cnt++;}//继续遍历下一个点，通知记录不合法的点数else{i = next;next++;}//遇到合法的点就令当前的上一个点变成遍历到的这个点}return n - cnt >= c;//总点数减去非法点就是合法点的数量
}
int main()
{while (~scanf("%d%d", &n, &c)){memset(dis, 0, sizeof(dis) / sizeof(int));for (int i = 1; i <= n; i++){scanf("%d", &dis[i]);}sort(dis + 1, dis + n + 1);		int l = 0, r = dis[n]-dis[1], mid, ans;while (l<=r){mid = (l + r) >> 1;if (check(mid)){//如果合法点数比要求的多，那就让间距再大一点ans = mid;l = mid + 1;}else//如果合法点数不够，就让间距再小一点r = mid - 1;}cout << ans << endl;}return 0;
}

13.2524 宗教信仰

描述
世界上有许多宗教，你感兴趣的是你学校里的同学信仰多少种宗教。
你的学校有n名学生（0 < n <= 50000），你不太可能询问每个人的宗教信仰，因为他们不太愿意透露。但是当你同时找到2名学生，他们却愿意告诉你他们是否信仰同一宗教，你可以通过很多这样的询问估算学校里的宗教数目的上限。你可以认为每名学生只会信仰最多一种宗教。

输入
输入包括多组数据。
每组数据的第一行包括n和m，0 <= m <= n(n-1)/2，其后m行每行包括两个数字i和j，表示学生i和学生j信仰同一宗教，学生被标号为1至n。输入以一行 n = m = 0 作为结束。
输出
对于每组数据，先输出它的编号（从1开始），接着输出学生信仰的不同宗教的数目上限。
样例输入
10 9
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
1 10
10 4
2 3
4 5
4 8
5 8
0 0
样例输出
Case 1: 1
Case 2: 7

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;#define MAX 50005
int kind[MAX];int find(int k) {if (k == kind[k])return k;else return kind[k] = find(kind[k]);
}void unite(int x, int y) {kind[find(x)] = find(y);
}int main() {int n, m, i = 1;while (1) {cin>>n>>m;if(m==0&&n==0) break;int res = 0;for (int i = 1; i <= n; i++)kind[i] = i;while (m--) {int a, b; cin >> a >> b;unite(a, b);}for (int i = 1; i <= n; i++) {if (find(i) == i) res++;}printf("Case %d: %d\n", i++, res);}
}

14.