---

前言

本章讲讲解图像处理相关内容，包括图像金字塔、图像轮廓模板提取、直方图、图像傅里叶变换等。

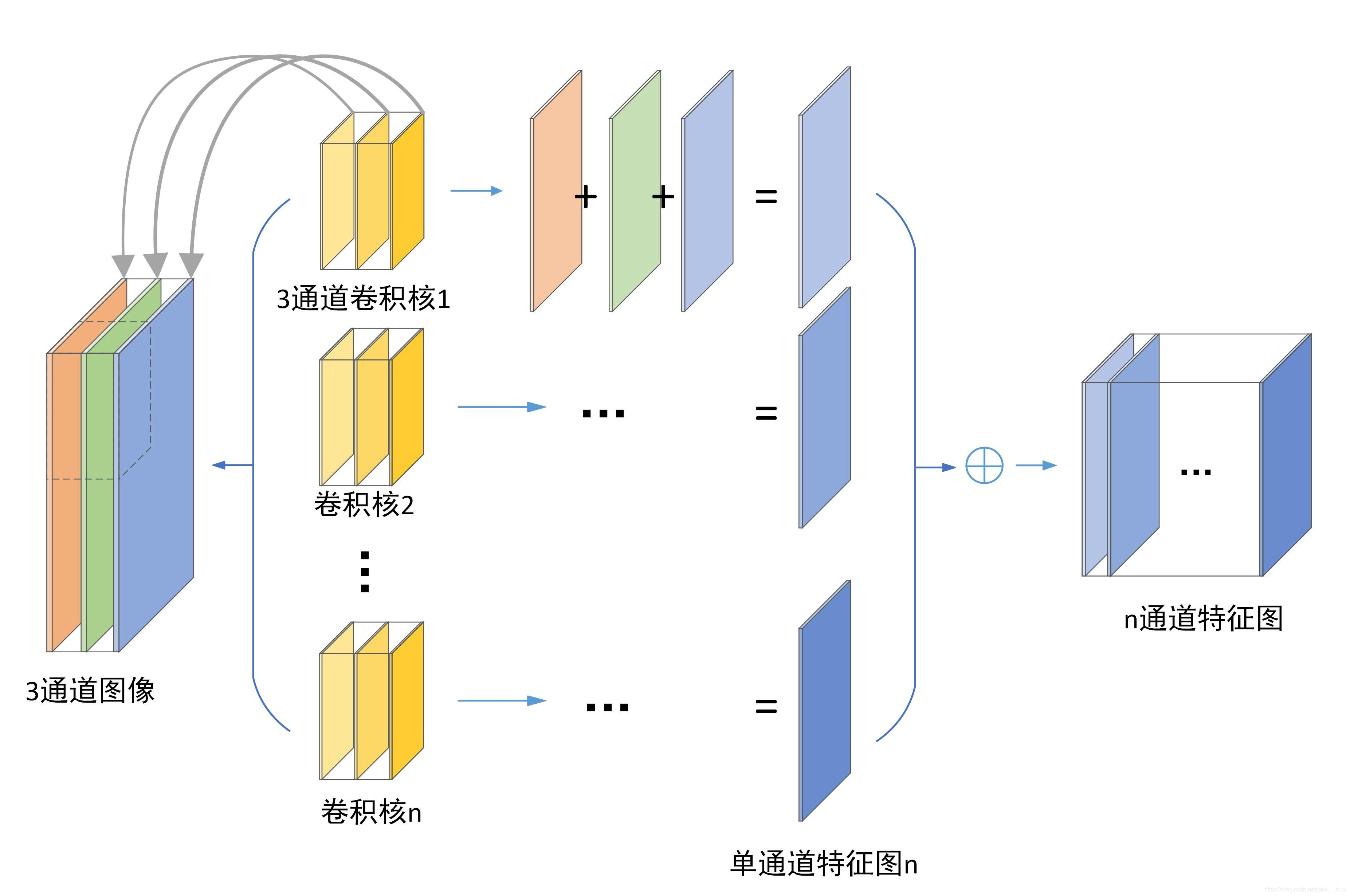
一、图像金字塔

• 含义： 图像金字塔是一种用于图像处理和计算机视觉的技术。它是一系列图像的集合，其中每个图像比前一个图像分辨率更低, 从而形成一种金字塔形的结构。这些图像可以由同一图像的不同分辨率版本生成，也可以是不同图像之间的扫描和缩小。
• 作用： 在图像增强中，可以将图像分解为一系列不同分辨率的图像，然后对每个分辨率级别的图像进行处理，最终将它们合成为一张增强后的图像。在图像检测中，可以使用金字塔技术进行对象的尺度不变性检测。在目标跟踪中，可以在不同的尺度上搜索目标。
  

1.高斯金字塔

• 向下采样（缩小 图片）：
  1. 首先进行高斯滤波
  2. 去除偶数的行、列
• 向上采样（放大图片）：
  1. 用零填充偶数行、列
     $$\left[\begin{array}{cc}10& 30\\ 56& 96\end{array}\right]\Rightarrow \left[\begin{array}{cccc}10& 0& 30& 0\\ 0& 0& 0& 0\\ 56& 0& 96& 0\\ 0& 0& 0& 0\end{array}\right]$$
  2. 对放大的图片进行高斯卷积，从而可对零值进行填充

# 向上采样
cv2.pyrUp(src[, dst[, dstsize[, borderType]]]) -> dst
# 向下采样
cv2.pyrDown(src[, dst[, dstsize[, borderType]]]) -> dst

2.拉普拉斯金字塔

$$I_{i+1}=I_i-PyrUp(pyrDown(I_i))$$
执行上面的公式，就能得到每一层的图像。

拉普拉斯金字塔和高斯金字塔是图像金字塔的两个重要概念，它们之间有以下不同点：

1. 算法步骤不同：高斯金字塔是由原始图像不断进行下采样（降分辨率）和高斯滤波得到的，每次下采样都将图像的尺寸减半。而拉普拉斯金字塔则是由高斯金字塔依次上采样（放大）和减去对应的低分辨率图像得到的。

2. 不同的金字塔目的：高斯金字塔主要用于图像降采样（缩小）和尺度空间分析，可以用于图像的尺度不变性特征描述，如SIFT、SURF算法等。拉普拉斯金字塔则主要用于对图像进行增强、边缘检测和图像融合等操作。

3. 金字塔层数和大小：高斯金字塔的层数与原始图像的大小有关，尺寸越大，高斯金字塔的层数也就越多。而拉普拉斯金字塔通常与高斯金字塔大小相同，因为它是由高斯金字塔得到的。

4. 局部特征信息：尽管可逆性和单尺度不变性有用，但仅仅用于描述局部特征时可能不够准确。因此，拉普拉斯金字塔通常能够提供比高斯金字塔更丰富的局部特征信息。

因此，根据不同的应用场景，可以选择高斯金字塔或拉普拉斯金字塔等适合的金字塔结构来处理图像。

二、图像轮廓

1. 轮廓提取

contours, hierarchy = cv2.findContours(image, mode, method[, contours[, hierarchy[, offset]]])

其中：

• image：输入的图像，应该是二值图像，每个像素的值要么为0，要么为255，表示前景和背景两种颜色。
• mode：轮廓检索模式，是一个枚举值，取值范围包括：
  • cv2.RETR_EXTERNAL：只检测最外层的轮廓，即只返回边缘轮廓；
  • cv2.RETR_LIST：检测所有的轮廓，并返回其完整的列表；
  • cv2.RETR_CCOMP：检测所有的轮廓，但只返回两级轮廓结构，即外层轮廓和内层轮廓；
  • cv2.RETR_TREE：检测所有的轮廓，并返回完整的轮廓树结构。
• method：轮廓近似方法，是一个枚举值，取值范围包括：
  • cv2.CHAIN_APPROX_NONE：存储所有的轮廓点，每个点的坐标（x,y）都存储；
  • cv2.CHAIN_APPROX_SIMPLE：仅保留轮廓的端点，只需存储它们的坐标即可，例如矩形轮廓仅需要4个点的坐标即可。
• contours：输出参数，返回检测到的轮廓，每个轮廓是一个由像素坐标表示的Numpy数组。
• hierarchy：输出参数，返回轮廓的层级关系，每个轮廓由4个值(父级轮廓编号，下一级轮廓编号，第一个子级轮廓编号，前一个兄弟轮廓编号)表示。
  hierarchy的理解

2. 轮廓绘制

cv2.drawContours()是OpenCV提供的一个函数，能够在图像中绘制轮廓。

该函数的语法如下：

cv2.drawContours(image, contours, contourIdx, color, thickness=None, lineType=None, hierarchy=None, maxLevel=None, offset=None)

参数解释如下：

• image: 要绘制轮廓的图像。
• contours: 一个由轮廓点集组成的列表，可以通过cv2.findContours()函数获取。该参数可以是一个单独的轮廓(Point集合)，也可以是多个轮廓的列表。
• contourIdx: 指定要绘制的轮廓的编号。如果是负数，则表示要绘制所有的轮廓。
• color: 轮廓颜色，可以是RGB元组或BGR元组。
• thickness: 轮廓线条粗细，默认值为1.
• lineType: 线条类型，默认值为8-connectivity（即cv2.LINE_8），也可以设置为4-connectivity（即cv2.LINE_4）或CV_AA。
• hierarchy: 轮廓层级信息，可选参数。
• maxLevel: 可以绘制的轮廓的最大级别，可选参数。
• offset: 轮廓计算的偏移量，可选参数。

3. 轮廓特征

在OpenCV中，对于图像中的轮廓，有许多特征可以用来描述和分析这些轮廓。下面列出了一些主要的轮廓特征：

1. 轮廓面积：轮廓曲线所包含的面积大小，可以用cv2.contourArea()函数计算。

2. 轮廓周长：轮廓曲线的长度，可以用cv2.arcLength()函数计算。

3. 轮廓近似：通过降低轮廓点数目来近似表示轮廓形状，可以用cv2.approxPolyDP()函数进行处理。

4. 轮廓重心：轮廓曲线所包含区域的质心点坐标，可以用cv2.moments()函数计算。

5. 轮廓方向：轮廓曲线的方向，可以用cv2.fitEllipse()或cv2.minAreaRect()函数分别拟合椭圆或矩形来计算。

6. 轮廓凸包：包含轮廓曲线所有点的凸边形，可以用cv2.convexHull()函数计算。

7. 轮廓缺陷：凸包与轮廓曲线之间的差距，可以用cv2.convexityDefects()函数计算。

这些轮廓特征可以结合使用，用来分析图像中的轮廓形状和特征。在实际应用中，轮廓特征常常被用来进行目标检测、图像分类和图像识别等任务。

4. 轮廓近似

• 原理：
  首先连接A、B两点，然后在弧线AB上找一点，使得该点到直线AB上的距离最大，记该点为C，该距离为d，若d小于指定的数值，则用直线AB代替弧线AB，否则则以C为中间点，再分别判断弧线AC与弧线CB的近似。

在OpenCV中，cv2.approxPolyDP()函数可以对轮廓进行近似处理，以减少轮廓点的数量，简化轮廓曲线，从而提高图像处理的效率。该函数的语法如下：

cv2.approxPolyDP(curve, epsilon, closed[, approxCurve])

参数解释如下：

• curve: 输入的轮廓，一般是一个由点组成的列表或Numpy数组。
• epsilon: 指定近似程度，即对轮廓的最大误差。如果指定的距离小于epsilon，那么就会被认为是同一曲线上的点。
• closed: 指定是否是闭合曲线，如果为True，表示曲线是闭合的，否则为打开的曲线。
• approxCurve: 输出的近似轮廓，可以是numpy数组或空对象。如果不指定输出数组，则函数会返回近似轮廓的坐标点数组。

该函数的返回值表示的是近似轮廓的坐标点，可以通过对输出数组的大小来确定近似后曲线上的点的数量。epsilon的值受影响因素较多，需要根据具体情况进行设定。

近似处理的效果往往受到调节参数的影响，如果epsilon设置得过小，处理得过度，则可能会丢失重要的轮廓信息；如果epsilon设置得过大，则可能会保留过多的轮廓信息，增加了计算量，并且可能导致轮廓的误检和漏检等问题。因此，在进行轮廓近似时，需要根据具体情况进行参数的调适，以达到最佳的处理效果。

5. 轮廓标记

• 作用： 用一个形状（矩形、圆圈等）将轮廓标记出来。

# 背景画布
canvabg = img.copy()
# 获取轮廓
cnt0 = contours[0]
# 矩形边框
startx,starty,width,height = cv2.boundingRect(cnt0)
cv2.rectangle(canvabg,(startx,starty),(startx + width,starty + height),(0,255,0),2)
# 获取轮廓
cnt1 = contours[2]
# 圆圈外框
(cx,cy),radius = cv2.minEnclosingCircle(cnt1)
cv2.circle(canvabg,(int(cx),int(cy)),int(radius),(255,0,0),2)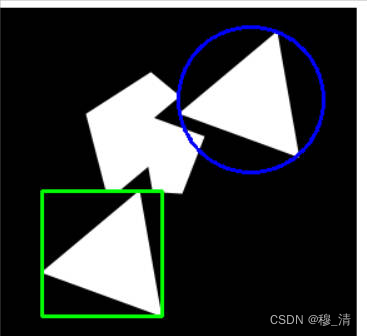

三、模板匹配

• 思路： 将模板图片当作卷积核与被匹配的图像进行卷积操作，然后根据具体匹配算法计算出每一步卷积操作的置信度，根据置信度来确定模板图像在被匹配图像中的位置。

在OpenCV中，使用cv2.matchTemplate()函数可以实现图像匹配的功能。图像匹配是指在一幅图片中查找某个感兴趣区域（通常是一个模板图像）在该图像中的位置和数量。

cv2.matchTemplate()函数的语法如下：

cv2.matchTemplate(image, templ, method[, result[, mask]]) → result

参数解释如下：

• image: 输入图像，应该是8位或32位浮点型的灰度图像。
• templ: 模板图像，在输入图像中查找的图像区域。与输入图像具有相同的数据类型和通道数。
• method:

  • 平方差匹配（cv2.TM_SQDIFF）：此匹配方法会依次比较输入图像和模板图像中像素点的差值平方，并返回差值的总和。匹配结果越小，匹配度越高。

  • 归一化平方差匹配（cv2.TM_SQDIFF_NORMED）：此匹配方法与平方差匹配方法类似，但会将匹配结果归一化，即匹配结果越小，匹配度越高。

  • 相关匹配（cv2.TM_CCORR）：此匹配方法将输入图像和模板图像进行互相关运算，并返回相关系数的最大值。匹配结果越大，匹配度越高。

  • 归一化相关匹配（cv2.TM_CCORR_NORMED）：此匹配方法与相关匹配方法类似，但会将匹配结果归一化，即匹配结果越大，匹配度越高。

  • 系数匹配（cv2.TM_CCOEFF）：此匹配方法会计算输入图像和模板图像之间的相关系数，然后从相关系数图像中找到最大值。匹配结果越大，匹配度越高。

  • 归一化系数匹配（cv2.TM_CCOEFF NORMED):计算归一化相关系数，计算出来的值越接近1，越相关。

• result: 匹配结果，一般不需要指定该参数，函数会自动创建。其大小为输入图像大小减去模板图像大小加1，是一个二维数组。
• mask: 遮罩，如果指定，则只在遮罩区域内进行模板匹配。

import numpy as np
import cv2
import matplotlib.pyplot as pltimg = cv2.imread("F:/MyOpenCV/ai.jpg")
imgTmp = cv2.imread("F:/MyOpenCV/aitemp.jpg")result = cv2.matchTemplate(img, imgTmp, cv2.TM_SQDIFF_NORMED)
minVal, maxVal, minLoc, maxLoc = cv2.minMaxLoc(result)
x, y = minLoc
h, w, t = imgTmp.shape
cv2.rectangle(img, minLoc, (x + w, y + h), (255, 0, 0), 2)cv2.imshow("img", img)
cv2.imshow("imgsim", imgTmp)
cv2.waitKey(0)
cv2.destroyAllWindows()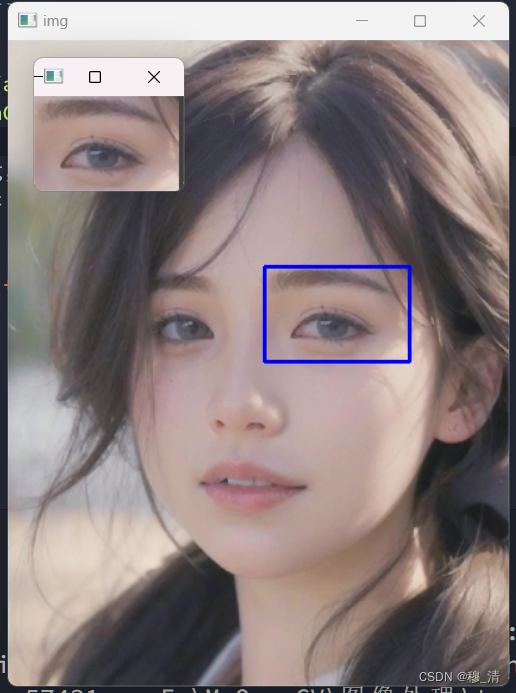

四、直方图

1. 对比度

• 定义： 对比度是指图像中最亮和最暗区域之间的差异度量，即白和黑之间的差异程度。在数字图像处理中，对比度可用于调整图像的明暗程度，通常是通过调整图像中像素的亮度和颜色值来实现。较高的对比度可以使图像更加清晰明亮，而较低的对比度则会使图像显得柔和、模糊或无法分辨。

2. 绘制直方图

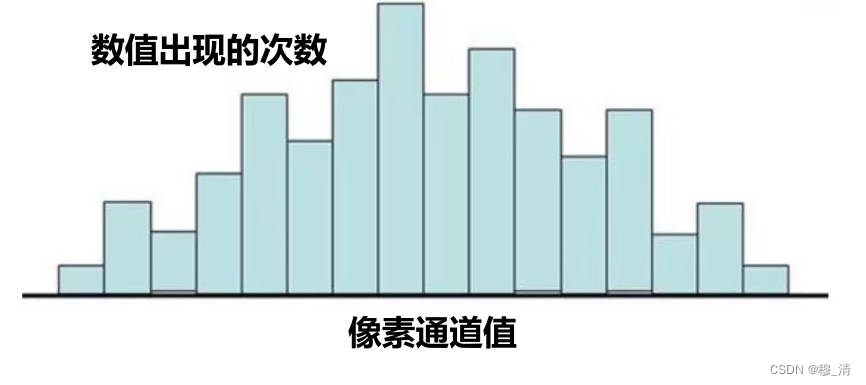
直方图的横坐标为像素通道值的取值范围，纵坐标为数值出现的次数。

cv2.calcHist() 可以用于计算灰度图像的直方图，也可以用于计算彩色图像的直方图。

cv2.calcHist() 的语法如下：

hist = cv2.calcHist(images, channels, mask, histSize, ranges[, hist[, accumulate]])

参数说明如下：

• images: 输入的图像，以 numpy 数组的形式提供。如果要计算灰度图像的直方图，则 images 的维度应该是二维的，而对于彩色图像，则应该是三维的，其中第三维表示图像的颜色通道。传递给函数的图像应该是一个列表，即使你只使用单个图像，也要将图像包装在列表中。
• channels: 要统计的颜色通道的索引列表。对于灰度图像，此参数应该为 [0]，对于彩色图像，则通常是 [0, 1, 2] 表示三个颜色通道。
• mask: 可选的掩码图像，用于指定参与直方图计算的像素位置。只有在掩码图像中对应位置像素值为非零值时，才会将该位置的像素纳入直方图计算。
• histSize: 直方图的bin数量，也就是区间数量。该参数应该为一个列表，每个元素表示一个通道的bin数量。
• ranges: 直方图的像素值范围，也就是区间范围。该参数应该为一个列表，每个元素表示一个通道的像素值范围。
• hist: 可选的输出直方图数组对象。
• accumulate: 可选的累加标志。

cv2.calcHist() 的返回值是一个numpy数组，表示所计算的直方图。对于灰度图像，返回的是一维数组；对于彩色图像，返回的是一个三维数组，其中每个维度分别表示BGR三个通道的直方图。

img = cv2.imread("F:/MyOpenCV/hello.jpg")
b, g, r = cv2.split(img)
imgGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)histGray = cv2.calcHist([imgGray], [0], None, [256], [0, 256])# 绘制直方图
plt.plot(histGray)
plt.xlim([0, 256])
plt.xlabel("灰度值")
plt.ylabel("像素数量")
plt.show()

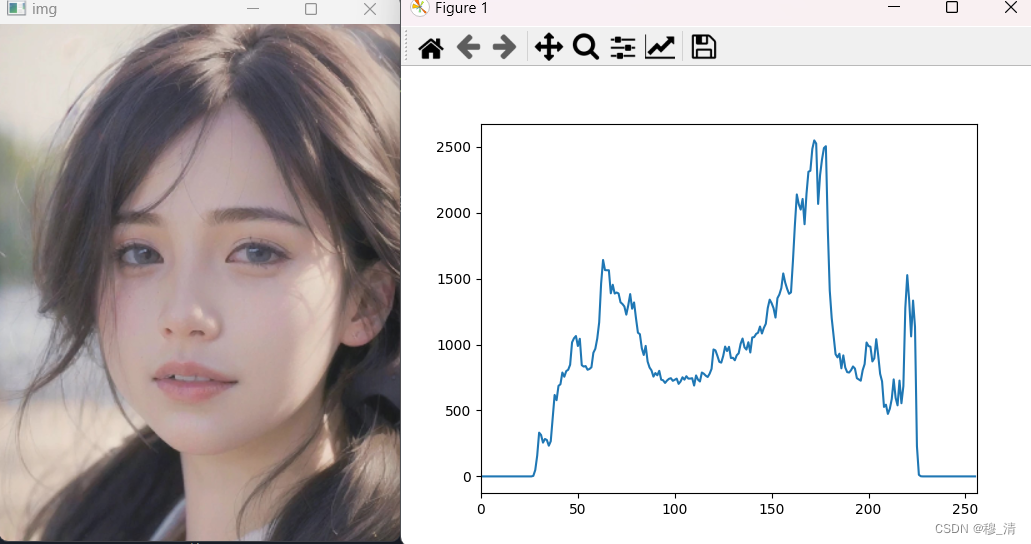
注：也可以使用matplotlib的方法，plt.hist(data, histSize)其中data为直方图的一维数组，因此图像数据调用ravel函数。

3. 均衡化

3.1 理论

• 目的： 将原图像通过变换，得到一幅灰度直方图的灰度值均匀分布的新图像。对在图像中像素个数多的灰度级进行展宽，而对像素个数少的灰度级进行缩减。从而达到清晰图像的目的。最理想的情况就是变换后，像素灰度概率完全一样的，但是实际上做不到那么平均。
  

3.2 代码

cv2.equalizeHist(src:image[, dst]) -> dst:image

4. CLAHE

• 直方图均衡化问题：

  • 全局效果，导致原来比较亮的地方变得更亮 原来暗的地方变得更暗 从而会导致细节的丢失。
  • 可能导致噪点的放大。

• 思路： 将图片进行拆分，然后分别对每个部分进行均衡化处理，且对每个部分的直方图概率分布做限制。

• 算法实现：

  1. 图像分块
  2. 找每个块的中心点
  3. 分别计算每个块的灰度直方图，并进行阈值限制
  4. 得到每个块的直方图分布后，根据直方图均衡化算法对每个块的中心点进行均衡化处理。只对中心点进行均衡化是为了加快计算速度。
  5. 根据中心点均衡化后的灰度值，利用差值算法计算图像块剩余像素的灰度值。

• 代码：

  # 生成自适应均衡化算法 
  # clipLimit ：阈值，1 表示不做限制。值越大，对比度越大
  # tileGridSize：如何拆分图像
  clahe = cv2.createCLAHE([, clipLimit[, tileGridSize]]) -> retval
  # 对像素通道进行自适应均值化处理
  dst = clahe.apply(src)

  cv2.createCLAHE 函数可接受三个参数，分别是 clipLimit、tileGridSize 和 tileGridSizeX（取代 tileGridSize），其中：

  • clipLimit：保持对比度等级的限制值，这个值越小，保持的对比度等级越高；
  • tileGridSize：将图像分成的矩形块的大小，以像素为单位。该参数应该是奇数。若在 tileGridSizeX 参数中指定，那么就不需要输入该参数。
  • tileGridSizeX：同 tileGridSize，用于指定矩形块的大小。

五、图像傅里叶变换

• 扩展阅读
  • 傅里叶变换
  • 二维傅里叶变换
  • 图像傅里叶

5.1 正弦平面波

• 直观定义： 将一维正弦曲线朝着纵向的一个方向上将其拉伸得到一个三维的波形，然后将波形的幅值变化用二维平面进行表示，再将二维平面波绘制成灰度图，从而波峰为255白色 波谷为0黑色，中间是一个灰度的过渡。
• 数学参数：
  • 正弦波：频率w， 幅值A，相位$\phi$
  • 拉伸方向：在二维坐标中，向量可以写为$\overrightarrow{n}=(\mu ,v)$

5.2 二维傅里叶变换

• 思想： 二维傅里叶变换中，认为二维数据是由无数个正弦平面波所构成。
  
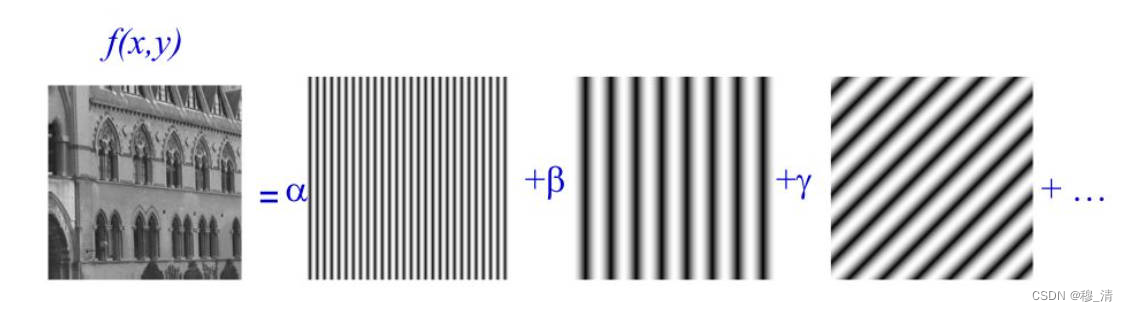
• 离散傅里叶变换公式：
  $$F(u,v)=\frac{1}{MN}\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}f(x,y)e^{-i2\pi (\frac{ux}{M}+\frac{vy}{N})}$$
• 参数的解释：
  

5.3 二维傅里叶变换结果$F(u,v)$

• (u, v)拉伸方向的向量
• $w=\sqrt{u^2+v^2}$ 向量的模表示正弦波的频率
• F(u, v)：复数， 隐含了正弦波的幅值A和相位$\phi$。详细的还是看上面的扩展阅读吧。

5.4 傅里叶变换的实现

OpenCV提供了dft(src:np.float[, dst[, flags[, nonzeroRows]]]) -> dst来进行傅里叶变换，参数含义如下：

• src：输入的单通道图像，必须为浮点型
• dst：输出的复数形式的结果，大小与src一致
• flags：变换操作的附加选项，通常可以设置为cv2.DFT_COMPLEX_OUTPUT表示输出为复数
• nonzeroRows：当输入图像的尺寸不是2的幂次方时，必须手动指定变换中心（如果输入图像大小为偶数，则默认中心为图像的中心，否则中心为左上角）
• n：可选参数，指定变换的大小，通常为src的尺寸
• 返回值是是双通道，第一个通道是实部，第二个通道是虚部

注：由于离散傅里叶变换具有共轭对称性 因此只有四分之一是有效的其他是翻转的。

• 频谱图中心化：
  方便用于滤波操作。

  # 频谱中心化
  shiftA = np.fft.fftshift(A)
  

5.5 傅里叶滤波

• 思路：
  1. 对图像灰度进行傅里叶变换，得到频域结果
  2. 将要删除的频率所对应的傅里叶变换结果全部置为0+i0
  3. 对修改后的傅里叶变换结果进行傅里叶反变换

5.5.1 低通滤波

将低频部分的结果全部置为零

import numpy as np
import cv2
import matplotlib.pyplot as pltimg = cv2.imread("F:/MyOpenCV/ai.jpg")
yuv = cv2.cvtColor(img, cv2.COLOR_BGR2YUV)
yfloat = np.float32(yuv[:, :, 0])  # 其实就是取了灰度图dft = cv2.dft(yfloat, flags=cv2.DFT_COMPLEX_OUTPUT)  # 生成频谱图
dftShift = np.fft.fftshift(dft)  # 中心化centerRow = int(dftShift.shape[0] / 2)  # 宽的中心
centerCol = int(dftShift.shape[1] / 2)  # 列的中心mask = np.zeros(dftShift.shape, dtype=np.uint8)  # 构造一个掩膜
mask[centerRow - 30 : centerRow + 30, centerCol - 30 : centerCol + 30, :] = 1
dftShift = dftShift * mask  # 按位乘dft = np.fft.ifftshift(dftShift)  # 先反中心化
idft = cv2.idft(dft)  # 再反傅里叶iyDft = cv2.magnitude(idft[:, :, 0], idft[:, :, 1])  # 转为实数
iy = np.uint8(iyDft / iyDft.max() * 255)  # 映射yuv[:, :, 0] = iy
imgRes = cv2.cvtColor(yuv, cv2.COLOR_YUV2BGR)cv2.imshow("imgRes", imgRes)cv2.waitKey(0)
cv2.destroyAllWindows()

5.5.2 高通滤波

类似于低通 改一下掩膜就行 效果如下（有点恐怖 下次还是使用灰度图吧）

总结

最近在忙实验室的项目，本篇搞的有点慢，这两天把它弄完。