今天又看了一便迪杰斯特拉算法,从非编程的角度上把这个算法又理解了一遍。其实这样来看的话,迪杰斯特拉算法和普利姆算法以及侧路斯卡尔算法刚开始的操作都是将点集分为U和V-U,这样的话便是在两个点集之间进行操作。迪杰斯特拉算法主要是这么做的:它不断的从d中找出边权值最小,而且尚未加入U的点,加入之后,再重新计算d和path的值,注意这里只计算那些V-U中的点,因为
已经加入U的点和源点之间的距离已经是最小的了,而且必定是不会改变的。这个我们要重点理解一下,因为第一次的时候U集合中只用源点一个点,下一个加进去的是和U直接距离最短的点。那么下一次再加进去的那个点,和源点的直接距离一定比第一次加进去的那个点要大,所以你没必要计算从源点到该点再加上从该点到第一次加进去的那个点的距离的和,因为这肯定是比从源点到第一次加进去的那个点之间的距离要大的。所以我们可以看到其实迪杰斯特拉算法根基其实也是落在第一次加进去的那个点的。这样的话我们不需要再下一步中去考虑U集合中的点,因为他们必定已经是最小的了。
相关文章
入职培训—中国电子信息产业发展研究院(赛迪集团)简介
中国电子信息产业发展研究院(China Center for Information Industry Development,简称研究院)是由中国电子工业发展规划研究院、信息产业部计算机与微电子发展研究中心(中国软件评测中心)、信息产业部电子信息中心、中国电子报社…
再会迪杰斯特拉(Dijkstra)
迪杰斯特拉算法
算法说明
迪杰斯特拉算法用来求解某一个起点到以其他所有点为终点的最短路径长度;
算法思路-贪心算法
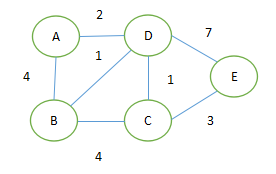
以下图为例 指定一个节点(即起点),例如计算“A”到其他节点的最短路径;引入两个集合(S,U&…
迪杰斯特拉算法(dijkstra)
算法背景:
图中的A,B,C,D,E,F,G,代表7个村庄,边上的权值带表两村庄之间的距离,现在要从某一个村庄,例如G村庄,往另外几个村庄送邮件,问G村庄到其他各村庄的最短距离分别是多少? 思路࿱…
算法之迪杰斯特拉算法
迪杰斯特拉(Dijkstra)算法是典型求单源(一个顶点到一个顶点)最短路径算法,用于计算一个结点到其他结点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
迪杰斯特拉算法思想
设G…
迪杰斯特拉算法(入门理解)
Dijkstra算法(求某一个点到其他点的最短距离):
*南昌理工学院ACM暑假集训队 😃 Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。 主要特点是以起始点为中心向外层层扩…