迪杰斯特拉(Dijkstra)算法是典型求单源（一个顶点到一个顶点）最短路径算法，用于计算一个结点到其他结点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

迪杰斯特拉算法思想

设G=(V,E)为一个带全有向图，把图中顶点集合V分成两组。第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将所到达最短路径的顶点加入到集合S中，直到全部顶点都加入到S中）。第二组为其余未确定最短路径的顶点集合（用U表示，U=V-S，U中的顶点不断的加入到S中，直到U为空，S=V）。在U加入S的过程中，始终保持源点到S中各顶点的最短路径长度小于或等于源点到U中任意顶点的最短路径长度。

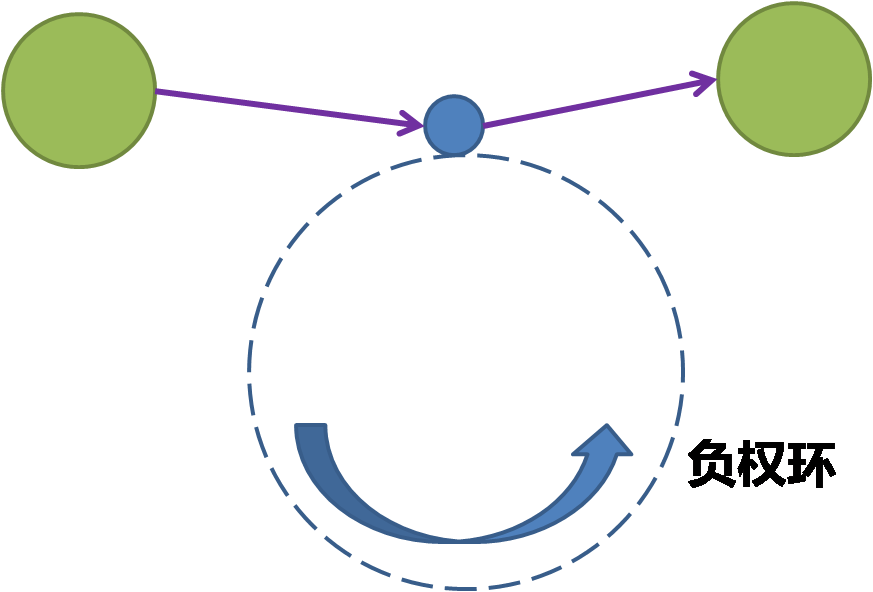
迪杰斯特拉算法要求边的权值不能为负数

迪杰斯特拉采用的贪心策略，设S集合中是已经计算出最短路径的节点，T集合中是未计算出最短路径的节点。假设存在负权，源点为A，已经计算出A->B的最短路径为m，若下一次将C添加进已计算出最短路径的节点集合，而A->C=m，C->B=-1，则会出现A->B的更短路径A->C->B，迪杰斯特拉不会对已经计算出最短路径的节点重新计算，因此无法更新最短路径，即负权的出现导致无法保证S中节点计算的是最短路径。

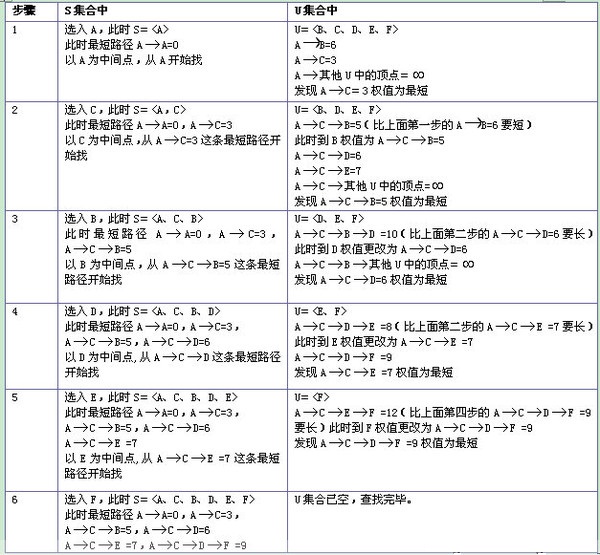
迪杰斯特拉算法步骤

1 定义个优先级队列，将起始顶点放入队列；

2 从队列里取出一个顶点，并设置该顶点已经访问

3 循环找到该顶点的邻接顶点 。 先统计邻节点所对应的路径权值，放入dis路径数组

4 从邻节点dis路径数组中找出dis的最小值， 下一次从未访问过、并且可以访问的最近的dis最短的结点开始(广度优先)；找到最小值后将此顶点放入优先级队列

5 重复直到优先级队列为空为止

迪杰斯特拉算法图解

动图
迪杰斯特拉算法在运行过程中 需要维持一组节点集合S,从源节点s到该集合每个节点之间的最短路径已经找到。算法重复从节点集合V-S中选择权值最小的节点u,将u设置已访问并加入到集合S. 然后从该顶点开始进行下轮寻找最小权值。其算法伪代码：

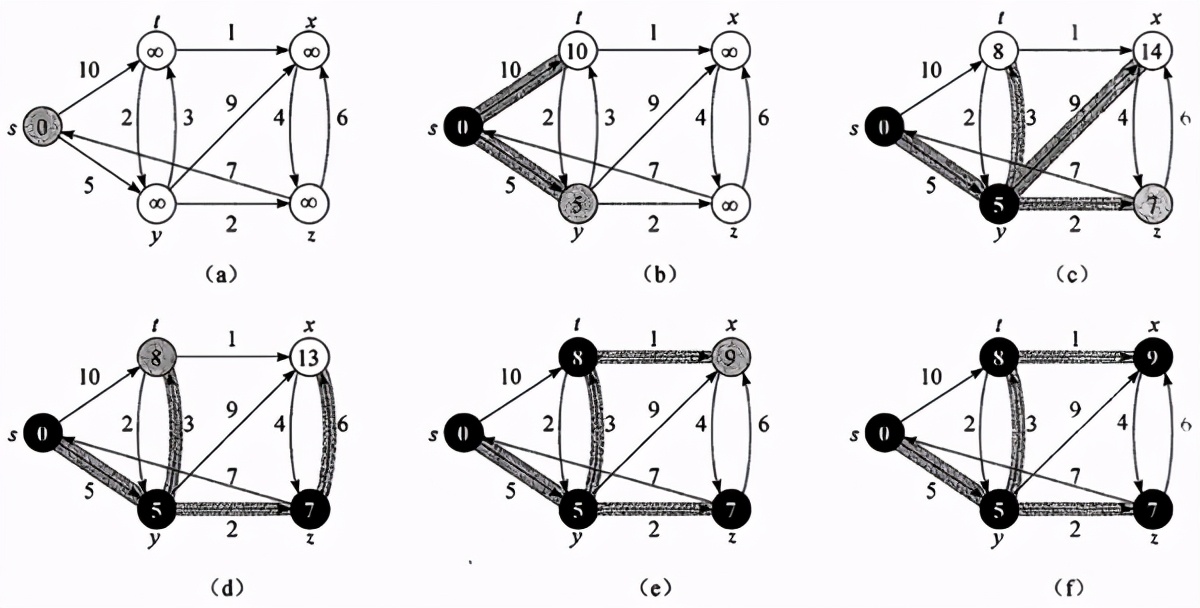
源节点s为最左边的节点，也就是我们设置的起始顶点，数值代表其边对应的权值。加阴影的边代表前驱值，黑色节点属于S集合，白色节点属于优先级队列里的节点；（a）为上图伪代码中4-8行循环首次执行的场景，阴影为节点距离值dis最小的节点，该节点在伪代码第5行被放入优先级队列 （b）-(f) 为成功执行while循环后的场景，所有图中加阴影的节点都是从优先级队列选出的节点作为下一次循环所用的节点；迪杰斯特拉算法每次都是从集合V-S中选择最近，权值最小的节点加入到集合S中，体现贪心策略。但是迪杰斯特拉不会对已经计算出最短路径的节点重新计算，因此无法更新最短路径，导致出现负权的无法保证S中节点计算的是最短路径。

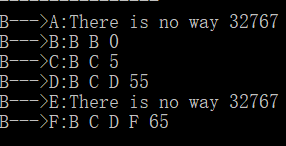
代码实现

图

class  DijkstraGraph{int[][] matrix;int vertexNum;public DijkstraGraph(int vertexNum) {this.vertexNum = vertexNum;matrix = new int[vertexNum][vertexNum];}public void addEdge(int start,int end,int weight){matrix[start][end] = weight;matrix[end][start] = weight;}}

迪杰斯特拉算法

 private   void  dijkstra(DijkstraGraph graph,int beginIndex){int minDistance = 0;dis[beginIndex] = 0;isVisited[beginIndex] = true;PriorityQueue<Integer> queue = new PriorityQueue<>();queue.offer(beginIndex);while (queue.size() > 0) {int  index = queue.poll();isVisited[index] = true;for (int j = 0; j < graph.vertexNum; j++) {if ( graph.matrix[index][j] != 0 && !isVisited[j]){//先统计邻节点所对应的路径权值//当有更短的路径方案时，替换路径值和方案dis[j] = Math.min(graph.matrix[index][j] + minDistance,dis[j]);}}minDistance = Integer.MAX_VALUE;for (int j = 0; j < dis.length; j++) {//从邻节点路径权值找出dis的最小值， 下一次从未访问过、并且可以访问的最近的dis最短的结点开始(广度优先)if(!isVisited[j] && dis[j] < minDistance) {minDistance = dis[j];index = j;}}if (!isVisited[index]) queue.offer(index);}}