迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)（BFS），直到扩展到终点为止

基本思想
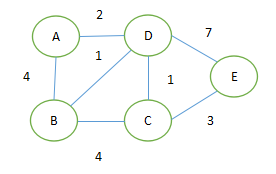
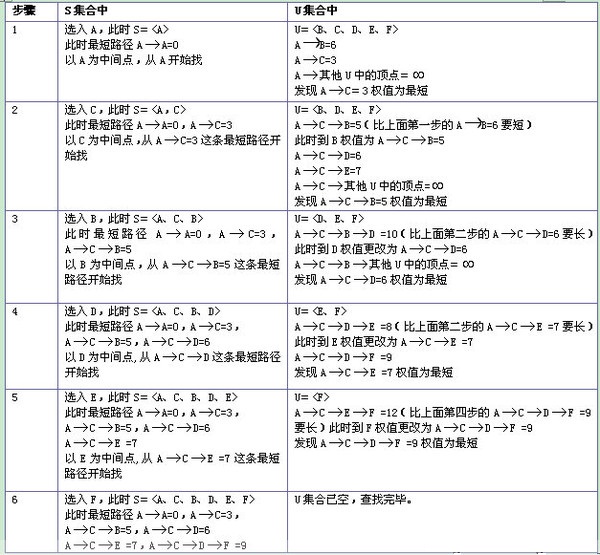
1.通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

2.此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

3.初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是”起点s到该顶点的路径”。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 … 重复该操作，直到遍历完所有顶点。

先将顶点D将入到S中，U中可以确定C，E的距离，其他都不确定距离

接着求顶点D到顶点C的最短路径，为3，加入到S中。C确定之后，可以更新B，F的距离

求出了E中的最短路径。这时候可以更新F，G的距离。

F的最短距离已确定，将其加入到S中。F确定之后，更新U中B，G的距离。

确定G的最短路径。可以更新U中A的距离

确定B的最短距离。可以更新A的距离。

确定A的最短距离

参考链接：https://blog.csdn.net/qq_37796444/article/details/80663810