1.问题

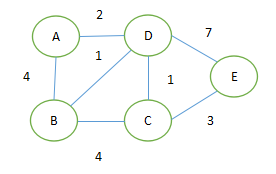
对于下图使用Dijkstra算法求由顶点a到顶点h的最短路径

解析
Dijkstra算法：从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

1.s=,T=v-s=<剩下顶点>，T中顶去对应距离
若存在 <v0,vi> d<v0,vi> 为对应的权重
不存在 <v0,vi> d<v0,vi> 为无限
2.从下中选取s中顶点有关联边企鹅权值最小顶点k，加入s
3.修改T在顶点距离值，若加入k，从v0到vidistanc↓ 则修改
重复2、3知道k=vi

#include<stdio.h>
#include<stdlib.h>
int i, j, n, m, max = 10000, sum, x, y, z, k;
int a[100][100], d[100], p[100];
int main()
{scanf("%d%d", &n, &m);for (i = 1; i <= m; i++){scanf("%d%d%d", &x, &y, &z);a[x][y] = z;}for (i = 1; i <= n; i++) {d[i] = max;}d[1] = 0;for (i = 1; i <= n; i++){sum = max;for (j = 1; j <= n; j++) {if (!p[j] && d[j] < sum){sum = d[j];k = j;}}p[k] = 1;for (j = 1; j <= n; j++) {if (a[k][j] != 0 && !p[j] && d[j] > d[k] + a[k][j])d[j] = d[k] + a[k][j];}}printf("a->");for (i = 2; i < n; i++) {printf("%d->", d[i]);}printf("%d\n", d[n]);return 0;
}