Dijkstra算法(求某一个点到其他点的最短距离):
*南昌理工学院ACM暑假集训队 😃
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
1.算法思想:
*设G=(V,E)是一个带权无向图,把图中节点分为两类,一类为已求出最短路径的节点集合S(初始时只有一源点V),另一类为未确定最短路径的节点集合U(利用一个book数组记录节点是否已求出最短路径,直到所有节点都被记录,算法就结束了)
*按最短路径长度的递增次序依次把U中节点加入到S中(通俗点来说就是,将S中已经找到最短路径的节点当作中间节点,根据U中其余各节点到源点的最短路径长度排序查找,路径越短越先被找到,并保持S中各节点到源点V的最短路径长度不大于源点V到U中任何节点的最短路径长度)。
2.算法步骤:
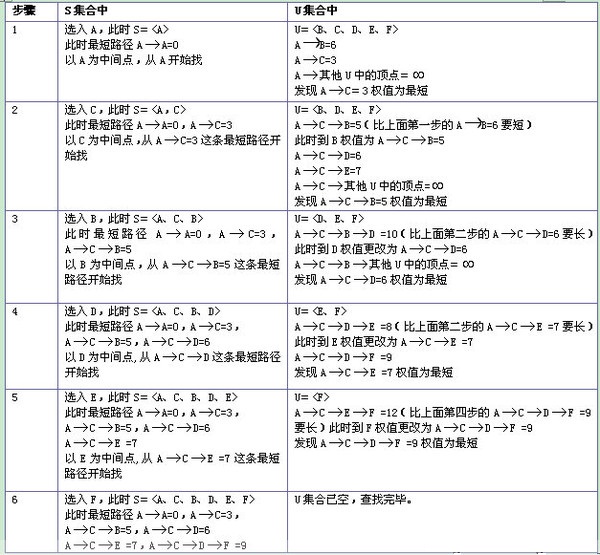
Ⅰ.初始化,构建邻接阵mp,节点到自身的距离为0,到其他节点之间若有边,则正常输入权值;反之,节点之间权值为∞。并创建数组dis,保存各节点到源点的距离。
Ⅱ.每次从U中选取距离上一个节点路径最小的节点(并在book数组中标记已选节点,防止重复选择),比较该节点到源点的距离和通过上一节点(中间节点)到源点的最短距离的距离大小,保存最小的为该节点到源点的最短路径(更新dis)。
Ⅲ.重复步骤,直到所有节点被标记。
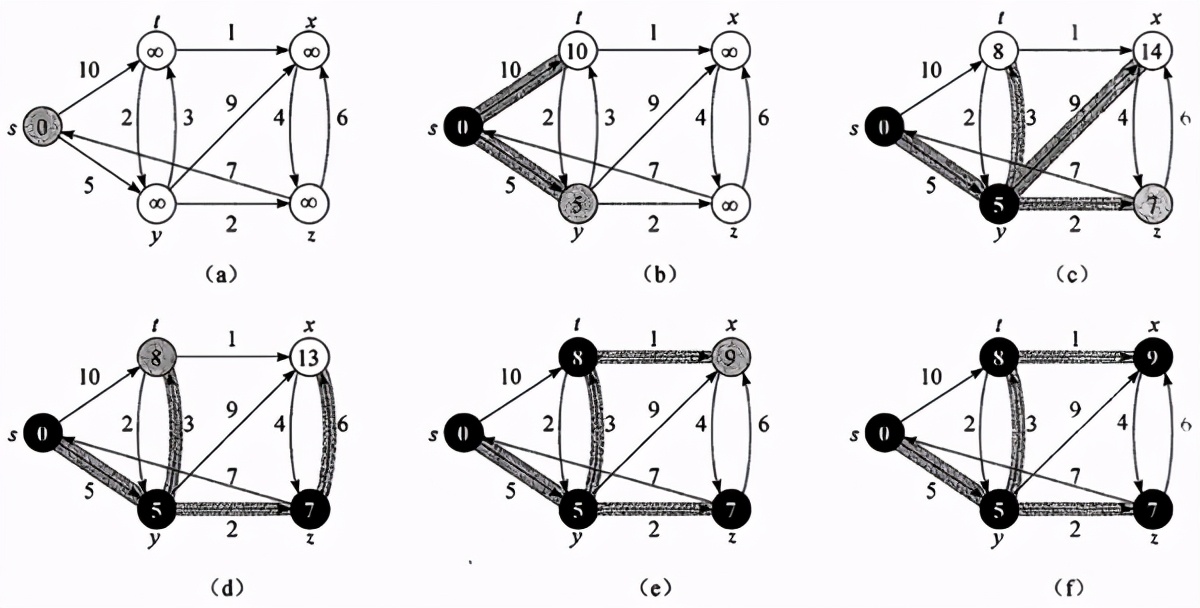
执行动画过程如下所示:
有一个带权无向图,由a(1节点)到b(5节点)的最短路径。每次找离上一节点最短距离的节点,依次递增。

如果你的思维已经跟得上动图的转换,就可以离开了
例题:
http://acm.hdu.edu.cn/showproblem.php?pid=2544 (hdu2544最短路)
题目大意:
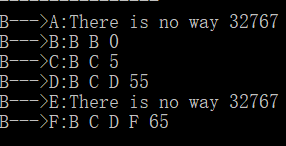
给定节点数和边数,以及各边所带的权值,求一条最短路。
代码如下(c语言):
#include<stdio.h>
#include<string.h>#define maxn 1010
#define INF 0x3f3f3f3fint n,m;
int dis[maxn],book[maxn],mp[maxn][maxn];//分别储存最短距离,节点是否取过, 邻接矩阵;void dj()
{int i,j;for( i=1; i<=n; i++ )dis[i]=ma[1][p];for( i=1; i<=n-1; i++ )//循环n-1次;{int min=INF,u;for( j=1; j<=n; j++ )//寻找与上一点距离最短的节点;{if( book[j]==0 && dis[j]<min ){min=dis[j];u=j;}}book[u]=1;for( j=1; j<=n; j++ )//找到后通过这个点更新其余的点到起点的距离{if( book[j]==0 && dis[u]+mp[u][j]<dis[j] )dis[j]=dis[u]+mp[u][j];}}printf("%d\n",dis[n]);
}int main()
{int i,j;int a,b,w;while( ~scanf("%d %d",&n,&m) && n+m )//当n=m=0时结束;{for( i=1; i<=n; i++ )//下标从0还是从1开始由题意决定;for( j=1; j<=n; j++ )//对邻接矩阵初始化;{if( i==j )mp[i][j]=0;elsemp[i][j]=INF;}memset(book,0,sizeof(book));for( i=1; i<=m; i++ ){scanf("%d %d %d",&a,&b,&w);if( w<mp[a][b] )mp[a][b]=mp[b][a]=w;}dj();}
}