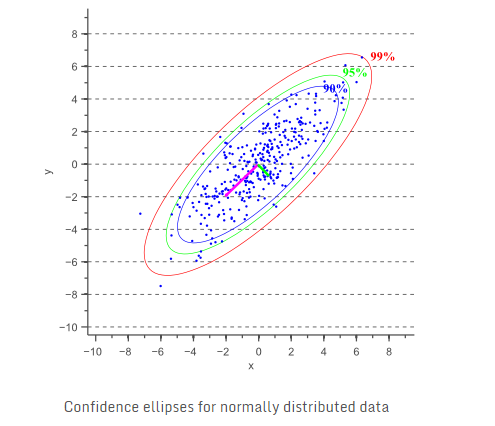
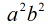最近工作中遇到了有关椭圆拟合的问题,把在这一过程中踩坑和最后使用的方法进行了总结。
参考链接:https://github.com/seisgo/EllipseFit
https://github.com/xiamenwcy/EllipseFitting
opencv3.2的方法
首先使用的是opencv的方法,该方法有时候会失效。
//待拟合的点
vector<Point> vpfinalfit = dangerzone;//把点的数量限制到20个
int interval = floor(vpfinalfit.size() / 20.0);
if (interval > 1)
{vector<Point> vpsample;for (int i = 0; i < vpfinalfit.size(); i += interval){vpsample.push_back(vpfinalfit[i]);}vpfinalfit = vpsample;
}//把坐标输出的文件中,在matlab中拟合
ofstream fout3;
fout3.open("data3.txt");
for (unsigned long i = 0; i < vpfinalfit.size(); i++)
{fout3 << vpfinalfit[i].x << " " << vpfinalfit[i].y << endl;
}
fout3.close();//使用椭圆拟合的方法
RotatedRect rr;
if (vpfinalfit.size() > 5)
{rr = fitEllipse(vpfinalfit);ellipse(src, rr, Scalar(0, 0, 0), 4);
}
拟合较好的结果

拟合不对的结果

matlab的方法(BFisher方法)
参考链接 http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/FITZGIBBON/ELLIPSE/
参考文献:Andrew W. Fitzgibbon, Maurizio Pilu, and Robert B. Fisher Direct least-squares fitting of ellipses, IEEE Transactions on Pattern Analysis and Machine Intelligence, 21(5), 476–480, May 1999
同样的点,在matlab中进行拟合,则可以实现较好的效果。
x = load('data3.mat');
p0=[0.005 0.005 0.005 0.005 0.005 0.005];
warning off
F=@(p,x)p(1)*x(:,1).^2+p(2)*x(:,1).*x(:,2)+p(3)*x(:,2).^2+p(4)*x(:,1)+p(5)*x(:,2)+p(6);
% ???????????
p=nlinfit(x,zeros(size(x,1),1),F,p0);A=p(1)/p(6);
B=p(2)/p(6);
C=p(3)/p(6);
D=p(4)/p(6);
E=p(5)/p(6);X_center = (B*E-2*C*D)/(4*A*C - B^2);
Y_center = (B*D-2*A*E)/(4*A*C - B^2);
fprintf(' X_center=%g, Y_center=%g\n',X_center,Y_center);a= 2*sqrt((2*A*(X_center^2)+2*C*(Y_center^2)+2*B*X_center*Y_center-2)/(A+C+sqrt(((A-C)^2+B^2))));
b= 2*sqrt((2*A*(X_center^2)+2*C*(Y_center^2)+2*B*X_center*Y_center-2)/(A+C-sqrt(((A-C)^2+B^2))));q=0.5 * atan(B/(A-C));
fprintf(' q=%g\n',q);fprintf(' a=%g, b=%g\n',a,b);
plot(x(:,1),x(:,2),'ro');hold on;
xmin=min(x(:,1));
xmax=max(x(:,1));
ymin=min(x(:,2));
ymax=max(x(:,2));
% 作图ezplot(@(x,y)F(p,[x,y]),[xmin,xmax,ymin,ymax]);
title('曲线拟合');
legend('采样点','拟合结果')

c++版本(BFisher方法)
该方法也有c++的版本,但是lapack的配置比较复杂。
DirectEllipseFit拟合的类定义,具体的代码可以去CSDN下载,稍后会上传,命名分别为myEllipse.h和myEllipse.cpp
template <typename T>
class DirectEllipseFit
{
public:DirectEllipseFit(const vector<T>& xData, const vector<T>& yData);Ellipse doEllipseFit();private:T getMeanValue(const vector<T>& data);T getMaxValue(const vector<T>& data);T getMinValue(const vector<T>& data);T getScaleValue(const vector<T>& data);vector<T> symmetricNormalize(const vector<T>& data);//Make sure xData and yData are of same sizevector<T> dotMultiply(const vector<T>& xData, const vector<T>& yData);//Get n*6 design matrix D, make sure xData and yData are of same sizevector<vector<T> > getDesignMatrix(const vector<T>& xData,const vector<T>& yData);//Get 6*6 constraint matrix Cvector<vector<T> > getConstraintMatrix();//Get 6*6 scatter matrix S from design matrixvector<vector<T> > getScatterMatrix(const vector<vector<T> >& dMtrx);//Transpose matrixvector<vector<T> > transposeMatrix(const vector<vector<T> >& mtrx);//Do matrix multiplication, mtrx1: j*l; mtrx2: l*i; return: j*ivector<vector<T> > doMtrxMul(const vector<vector<T> >& mtrx1,const vector<vector<T> >& mtrx2);/*** @brief solveGeneralEigens: Solve generalized eigensystem* @note For real eiginsystem solving.* @param sMtrx: 6*6 square matrix in this application* @param cMtrx: 6*6 square matrix in this application* @param eigVV: eigenvalues and eigenvectors, 6*7 matrix* @return success or failure status*/bool solveGeneralEigens(const vector<vector<T> >& sMtrx,const vector<vector<T> >& cMtrx,vector<vector<T> >& eigVV);//Convert matrix expression from nested QVector to 1-order arraydouble* mtrx2array(const vector<vector<T> >& mtrx);/*** @brief calcEllipsePara: calculate ellipse parameter form eigen information* @param eigVV: eigenvalues and eigenvectors* @return ellipse parameter*/Ellipse calcEllipsePara(const vector<vector<T> >& eigVV);private:vector<T> m_xData, m_yData;
};
更简单的方法
如果你喜欢用最新版的软件,在opencv4.0以上的版本中,椭圆拟合函数增加了新的方法,其中有一个就是使用的上述方法,所有可以直接调用opencv4.0以上版本的库。
RotatedRect rr;
if (vpfinalfit.size() > 5)
{rr = fitEllipseAMS(vpfinalfit);//rr = fitEllipse(vpfinalfit);ellipse(src, rr, Scalar(0, 255, 255), 1); //画椭圆
}
但是不能盲目升级,就是因为这个原因,笔者把原来开发的Android程序jni使用的opencv版本从3.2升级到了4.0,导致队友原来开发的视觉算法编译通不过来,不过没有什么,从opencv3到opencv4大部分是是简单的变量命名替换,改起来还是比较轻松。