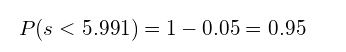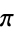误差椭圆

原文链接：https://blog.csdn.net/u010182633/article/details/45924061

介绍

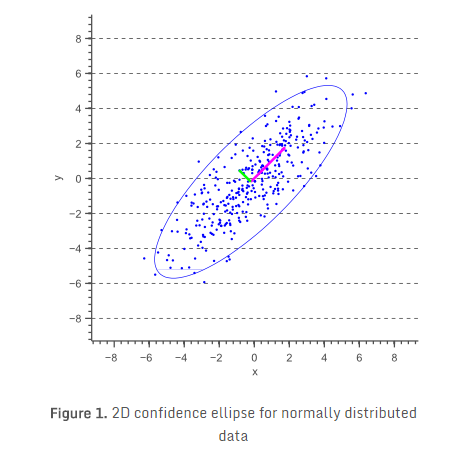
在这篇文章中，我将展示如何绘制二维正态分布数据的误差椭圆，又名置信椭圆。误差椭圆代表高斯分布的等值轮廓线，并允许可视化一个2D置信区间。下图显示了一组二维正态分布数据样本的95％置信椭圆。这个置信椭圆定义的区域包含了95％的样本，这些样本可以从潜在高斯分布中得到。

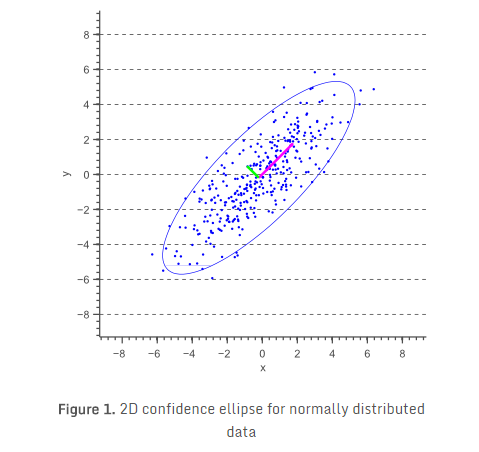
这里写图片描述
在接下来的章节中，我们将讨论如何获得不同置信度（如99％置信区间）的置信椭圆，我们将展示如何用Matlab或C ++代码绘制这些椭圆。

轴对齐的置信椭圆

导出得到误差椭圆的一般方法之前，我们先看看特殊情况，椭圆的长轴平行X轴，如下图：
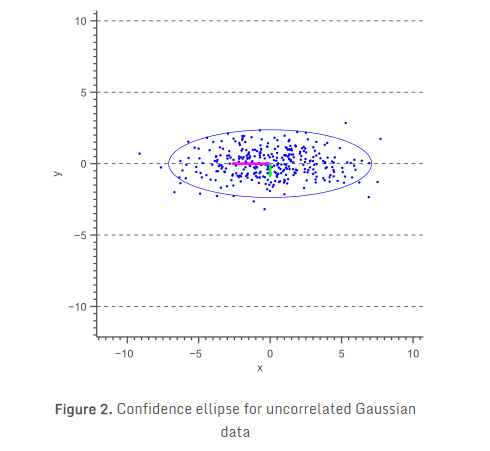
这里写图片描述
上图展示出了椭圆的角度由数据的协方差确定。在这种情况下，协方差为零，使得数据是不相关的，从而导致轴对齐误差椭圆。

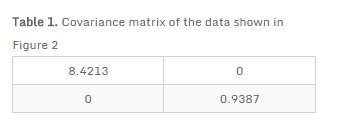
此外，椭圆轴的大小取决于数据的方差。在我们的例子中，X轴方向的方差最大，Y轴方向的方差最小。

一般情况下，长轴为2a，短轴为2b，原点为中心的轴对齐椭圆的方程式定义如下：
这里写图片描述

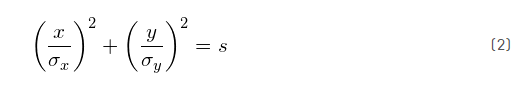
在我们的例子中，轴的长度由数据的标准差这里写图片描述定义，这样的话误差椭圆的方程式变为：

其中s定义椭圆的规模，可以是任意的数（例如，s=1）。现在的问题是如何选择s，使得所得到的椭圆规模代表我们所选择的置信水平（例如，95％的置信水平对应于s =5.991）。

我们的2D数据从零协方差的高斯分布中采样得到。这意味着x值和y值也是高斯分布。因此，等式（2）的左手侧实际上代表独立正态分布数据样本的平方和。根据所谓的卡方（Chi-Square）分布，高斯数据点平方的总和是已知的。卡方分布用“自由度”的形式定义，它表示未知量的数目来。在我们的例子中，有两个未知数，因此自由度是二。

因此，我们可以很容易地获取上述和的概率，通过计算卡方似然，s等于一个特定的值。事实上，由于我们感兴趣的是置信区间，我们正在寻找s小于或等于某个特定值的概率，这个特定值可以用累积卡方分布得到。由于统计人员都是懒惰的（这个翻译我也是醉了【好吧，其实就是我翻译的】原文为“As statisticians are lazy people”期待大家可以给出更好的翻译），我们通常无法尝试计算这个概率，而只是看一个概率表：https://people.richland.edu/james/lecture/m170/tbl-chi.html

例如，使用此概率表，我们可以很容易地发现，在2个自由度的情况下：
这里写图片描述

因此，95％置信区间对应于s=5.991。换言之，95％的数据将落入椭圆内：
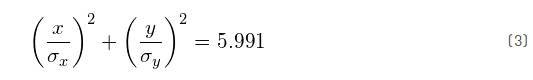
这里写图片描述
类似地，99％的置信区间对应为s=9.210，90％置信区间对应于s=4.605。

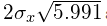
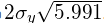
图2显示的误差椭圆可以绘制成长轴长度等于这里写图片描述，短轴长度。

任意置信椭圆

在数据是相关的情况下，例如存在协方差，所产生的误差椭圆不会是轴对齐的。在这种情况下，如果我们暂时定义一个新的坐标系，使得所述椭圆变为轴对齐，然后旋转所产生的椭圆，那么上面的结论依然有效。

换句话说，之前我们计算平行于x轴和y轴的方差，现在我们计算平行于置信椭圆长轴和短轴的方差，需要计算的方差方向由图1粉红和绿色箭头表示出来。
这里写图片描述

这些方向实际上是数据变化最多的方向，并用协方差矩阵定义。协方差矩阵可以看作是一个矩阵，该矩阵线性变换一些原始数据来获得当前观察到的数据。在之前特征向量和特征值的文章中，我们发现沿着这样一个线性变换的方向向量是变换矩阵的特征向量。事实上，图1中粉红色和绿色箭头所示的向量是数据协方差矩阵的特征向量，而向量的长度对应于特征值。

因此，特征值代表特征向量方向上数据的传播。换句话说，特征值代表特征向量方向上数据的方差。在轴对齐误差椭圆的情况下（即协方差等于零）特征值等于协方差矩阵的方差，特征向量等于x轴和y轴的定义。在任意相关数据的情况下，特征向量表示数据最大传播方向，而特征值定义这个传播有多大。

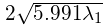
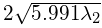
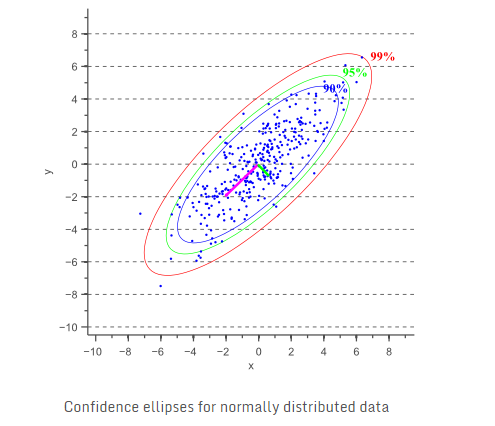
因此，95％置信椭圆可以类似地定义到轴对齐的情况，长轴长度为这里写图片描述，短轴长度为，其中λ1和λ2表示协方差矩阵的特征值。