目录
一,椭圆曲线
二,椭圆曲线上的有理点
1,y^2=x^3+x
2,y^2=x^3-4x^2+16
3,y^2=x^3+17
三,挠点系
1,挠点系
2,挠点系的意义
3,有理挠点系
4,挠定理
(1)Nagell-Lutz定理
(2)Mazur定理
四,椭圆曲线上的整点
1,挠点系和整点
2,y^2=x^3+17
3,Siegel定理
一,椭圆曲线
在椭圆曲线加密https://blog.csdn.net/nameofcsdn/article/details/115627882一文中,主要讨论的是,椭圆曲线的一些和加密相关的特性,
本文讨论其他的一些特性。
椭圆曲线加密中给出了常用椭圆曲线的方程
本文使用它规约之后的形式:
判别式: 如果
不为0那么它就是椭圆曲线。
参考:https://blog.csdn.net/nameofcsdn/article/details/105172343
本文不讨论加密,所以没有无穷远点。
二,椭圆曲线上的有理点
1,y^2=x^3+x
证明曲线上唯一的有理点是(0,0)
证明:假设存在其他有理解,设x=a/b,y=c/d
则
两边都是最简分数,所以
所以
所以
而这个方程其实是无解的,证明参考https://blog.csdn.net/nameofcsdn/article/details/115708334
所以没有其他有理解。
2,y^2=x^3-4x^2+16
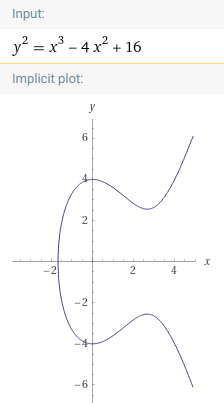
曲线上只有4个有理点:x=0或4,y=4或-4
这4个点连成的6条直线,有2条是垂直的,还有4条分别是这4个点处的切线,这6条直线都和曲线没有第三个交点。
3,y^2=x^3+17
曲线上有无穷多有理点
三,挠点系
椭圆曲线,其中a,b,c都是整数
1,挠点系
如果椭圆曲线上有t个点,t>=3,
且任意两点连成的直线,要么和曲线没有第三个交点,要么第三个交点就在这t个点中,
那么我们称,这t个点构成一个挠点系。
2,挠点系的意义
挠点系的存在告诉我们,通过连接直线寻找第三个点的方法,有可能只能找到有限个点。
3,有理挠点系
如果一个挠点系中都是有理点,那么我们称之为有理挠点系。
显然,2个有理点连成的直线,要么和曲线交于有理点,要么没有第三个交点。
所以,如果有理点的个数是有限的,那么所有的有理点就可以构成一个挠点系。
4,挠定理
如果椭圆曲线存在有理挠点系,判别式不为0,那么:
(1)Nagell-Lutz定理
该挠点系中所有点都是整点,且对于每个点,纵坐标y要么是0,要么满足
PS:有可能有整点不在挠点系中
(2)Mazur定理
该挠点系中至多只有15个点
PS:有理点要么不超过15个,要么有无穷多个。如果一个有理点不在任何一个挠点系中,那么有理点一定是无穷多的。
四,椭圆曲线上的整点
1,挠点系和整点
因为通过2个整点并不能直接得到一个新的整点(这和有理点不同),所以挠定理和整点关系不大。
有可能有整点不在挠点系中。
2,y^2=x^3+17
曲线上的整点(-2,3)不在任何一个挠点系中。
在x<10^100的范围内,所有的整点如下:
x=-1,-2,2,4,8,43,42,5234,一共16个点。
看起来似乎x大于5234的整点非常少,有可能没有了。
3,Siegel定理
椭圆曲线,其中a,b,c都是整数
如果判别式不为0,那么曲线上只有有限个整点


