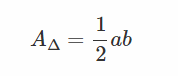原文链接：
https://www.lfhacks.com/t/draw-ellipse

在现实生活中如何画 椭圆 ？椭圆并不是由圆压扁而来，而是要符合一定的规则才能称为椭圆。现实生活中如果有画椭圆的需求，应该按照固定的方法作图。本文介绍一些绘制椭圆的方法。

焦点法
又叫园丁画法（gardener’s construction），因为在划定椭圆形花坛时，这个方法最为实用，而且画出的椭圆也足够标准。

与 椭圆的定义 所描述的一致，用一根没有弹性的绳，两端固定，可以做出椭圆。

• 优点：
  因为很长的绳子可以折叠，便于携带，所以这种方法可以画出很大的椭圆。

• 缺点
  现实中，绳子的粗细不能忽略，而且绳子越粗，这种方法越不精确

内旋轮线

如这篇 内旋轮线 所描述，当大小圆半径之比为 2:1 时，可以得到椭圆轨迹

这种方法需要半径比为2的两个圆相互啮合，比如 图斯双圆

参数方程法
观察 椭圆的参数方程 ：(x,y)=(acost,bsint)，刚好可以表示为一根线段上定点的轨迹。

如下图所示：

用一根长度为 a+b 的硬杆，两端在 x 轴、y 轴上滑动。到两端距离分别为 a 和 b 的点的横坐标总等于 acos(t) ，纵坐标总等于 bsin(t) 。所以这个点的轨迹即为椭圆，而且椭圆的长、短半轴分别为 a、b 。

图中的紫色表示滑块经过的轨迹，说明这种方法为了画出半轴为a,b的椭圆，需要两根长a+b轨道。

• 优点：
  能比 焦点法画椭圆 作出更为精确的椭圆轨迹
• 缺点：
  工具的尺寸(a+b)比画出的椭圆(a,b)更大，限制了这种方法的应用
  椭圆一周的轨迹，需要4次越过轨道，增加了画图的难度，有可能使椭圆不连续

参数方程法改进
注意到上面的 参数方程法 里，滑杆中点的坐标为
(a+b2cos(t),a+b2sin(t)),
刚好是个圆。所以，参数方法里的滑杆可以折叠起来，如下图。

与前面方法相比，少了一根轨道，减小了工具的体积，相当于将另一个根轨道的约束转化为圆心的约束。但仍然没有解决工具尺寸过大的问题。

椭圆规
常见的椭圆规，克服了上述的缺点，轨道更短，且椭圆曲线不与轨道相交。原理如下：

滑杆长度为a，两个滑块距离固定为a−b，则滑杆另一端点的轨迹仍然为(acos(t),bsin(t))，即椭圆方程。

轨道长度只需要a−b。

现实中的椭圆规长这样：

有趣的是，椭圆规的两根轨道是等长的，却画出了一个偏心的椭圆。

---

---

椭圆 | LFhacks.com
https://www.lfhacks.com/t/ellipse

椭圆的定义
椭圆是平面上到两个固定点的距离之和为常数的点之轨迹。

{P||PF1|+|PF2|=C}
下面的动图表示，到两个焦点的距离之和为常数。

椭圆的方程

从参数式可以看出：横坐标 x 来自半径 a 的圆，纵坐标 y 来自半径 b 的圆。

再进一步，从 正弦曲线 ，余弦曲线 与单位圆的联系 ，可以得出

椭圆是由相互垂直的两个振动的叠加。

即 利萨如图形 中，a:b=1:1 的情况。

圆变为椭圆
圆可以看做焦点重合的 椭圆。离心率 eccentricity

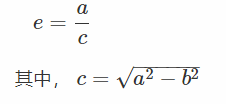
图中的绿色直线表示椭圆的准线（directrix）。准线的方程为
x=a2c
圆的准线可以看做位于无穷远，随着离心率 e 的增大，准线接近圆点。

椭圆的准圆
准圆 Director circle是椭圆外切矩形的外接圆。

准圆的半径是

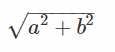
椭圆的切线方程
过点(x0,y0)的椭圆切线方程为

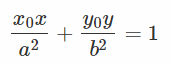
光学反射性质
从任一焦点发出的光线，反射光将通过另一个焦点。

共轭直径

共轭直径三角形

共轭直径构成的三角形，面积恒定为