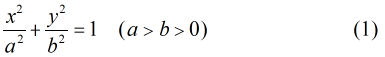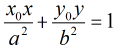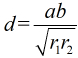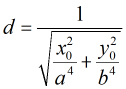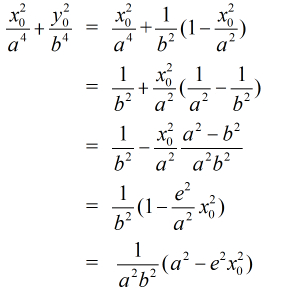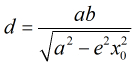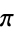本文将要讨论的是椭圆中心到椭圆切线的距离公式，在求这个距离之前，我们首先要知道两个定理。

 

定理1：椭圆

 

      

 

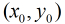
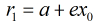
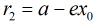
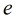
      上的点到椭圆左，右焦点的距离分别是和，其中是椭圆的离心率。

 

 

定理2：椭圆（1）上的点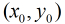处的切线方程是

 

     

 

实际上这两个定理都是很容易证明的，这是高中所学的知识，此处不再赘述。接下来我们来认识一个定理。

 

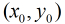
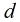
定理3：椭圆（1）的中心（也就是坐标原点）到以椭圆上的点为切点的切线的距离与椭圆的半长轴和半短

      周及焦半径的关系是

                      

 

现在我们来简略证明一下。

 

证明：由定理2可以知道

    

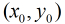
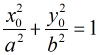
     又因为点在椭圆（1）上，那么有

 

     ，所以进一步得到

 

    

 

      所以继续得到

 

     

 

      又因为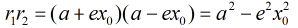，所以最终得到

 

     

 

题目：http://acm.hdu.edu.cn/showproblem.php?pid=2876

 

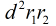
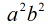
题意：求的值，那么答案也就是。

 

代码：

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>using namespace std;int main()
{int T;scanf("%d",&T);while(T--){double a,b,x,y;scanf("%lf%lf%lf%lf",&a,&b,&x,&y);if((x*x)/(a*a) + (y*y)/(b*b) < 1){printf("In ellipse\n");continue;}printf("%.0lf\n",a*a*b*b);}return 0;
}