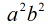问题描述

已知椭圆的长半轴a和短半轴b，以及椭圆的中心(xc,yc)，绘制椭圆像素图。

中点椭圆算法

中点椭圆算法与圆的绘制算法类似，也是在某一区域范围内，单位间隔取样，确定离指定椭圆最近的像素位置，然后通过椭圆的对称性，绘制其他像素点。对于椭圆中心不在原点处的情况，同样地我们通过平移将xc加到x，yc加到y，从而将计算出的每个位置(x,y)移动相应的屏幕位置。

与圆的对称性不同，椭圆在八分象限之间是不对称的，我们必须计算一个象限中椭圆曲线的像素位置，再由对称性得到其他三个象限的像素位置。

如下图所示，在第一象限内，当过椭圆上一点的斜率k>-1时，在x方向取单位步长，即从位置(0,b)开始，在第一象限沿椭圆路径，当前点取(xk,yk)时，x步进一个单位，判断下一点取(xk+1,yk)还是(xk+1,yk-1)；反之当k<-1时，在y方向取单位步长，当前点取(xk,yk)，判断下一点取(xk,yk+1)还是取(xk-1,yk+1)。因此我们需要按照k>-1和k<-1将第一象限的椭圆划分成两个区域讨论。

(注：我的文章都是用word写的，从word直接复制到博客，会出现很多格式问题，本人偷懒就直接从word截图粘贴到博客，阅读体验会降低，请谅解!)

                                                                                      图1 椭圆的处理区域

 

 

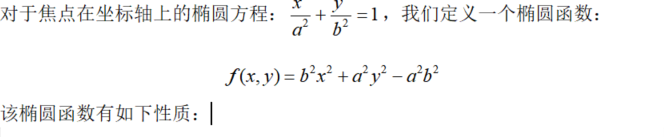
void ellipseMidPoint(const int xc, const int yc, const int a, const int b)
{int x = 0;int y = b;int p = round(b*b-a*a*b+0.25*a*a);int px = 0;int py = a*a*y;SetPixel(x+xc, y+yc);SetPixel(x+xc, -y+yc);while (px < py){if (p>0){p += (2*b*b*x - 2*a*a*y + 3*b*b + 2*a*a);y--;}else{p += (2*b*b*x + 3*b*b);}x++;px = b*b*x;py = a*a*y;SetPixel(x+xc, y+yc);SetPixel(x+xc, -y+yc);SetPixel(-x+xc, -y+yc);SetPixel(-x+xc, y+yc);}p = round(b*b*(x+0.5)*(x+0.5) + a*a*(y-1)*(y-1)-a*a*b*b);while (y>0){if(p<0){p += (b*b*(2*x+2)-a*a*(2*y-3));x++;}else{p += (3*a*a-2*a*a*y);}y--;SetPixel(x+xc, y+yc);SetPixel(x+xc, -y+yc);SetPixel(-x+xc, -y+yc);SetPixel(-x+xc, y+yc);}
}