首先我们很了解欧氏距离了，就是用来计算欧式空间（就是我们常见的坐标系）中两个点的距离的。
比如点 $x=(x_1,\dots ,x_n)$ 和 $y=(y_1,\dots ,y_n)$ 的欧氏距离为：
$$\begin{gathered} d(x,y)=\sqrt{(x_1-y_1{)}^2+(x_2-y_2{)}^2+...+(x_n-y_n{)}^2} \\ =\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2} \\ =\sqrt{(x-y{)}^T(x-y)} \end{gathered}$$

马氏距离多用在异常检测中，如下图所示，我们的数据是呈椭圆分布的，椭圆的中心点就是中间那个绿色的点。现在我们需要判断外面绿色点和蓝色点那个是离群点，哪个是正常点？

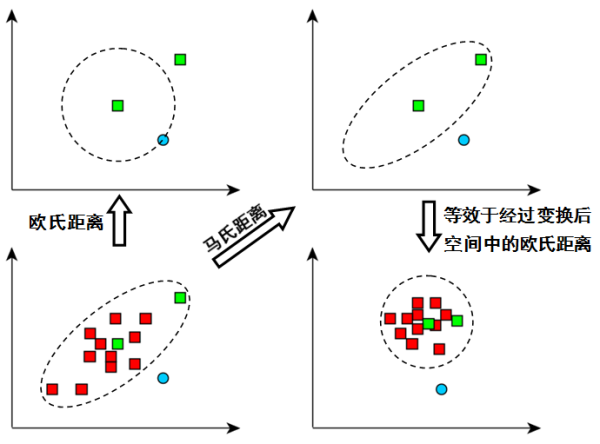
很明显绿色点在椭圆内，所以绿点应该是正常点，蓝点应该是离群点。但若用欧氏距离计算，蓝色应该是正常点。所以欧氏距离这时就出现了问题。

再举个一维的栗子，现在有两个类别，统一单位，第一个类别均值为1，方差为0.1，第二个类别均值为5，方差为4。那么一个值为2.5的点属于第一类的概率大还是第二类的概率大？

欧式距离上说应该是第一类，但是直觉上显然是第二类，因为第一类的数值范围在$1\pm 0.1$，第二类的数值范围为$5\pm 4$，所以肯定是第二类。

看出端倪了没？就是均值与方差问题。

在正式开始欧氏距离之前，希望你能有PCA的基础：PCA 主成分分析-清晰详细又易懂。这篇文章写得很清晰详细，建议先画十分钟将PCA看懂。

由这篇文章我们知道，可以将数据先减去均值进行中心化（图左），再进行基变换，将原数据映射为如下图右所示的数据。

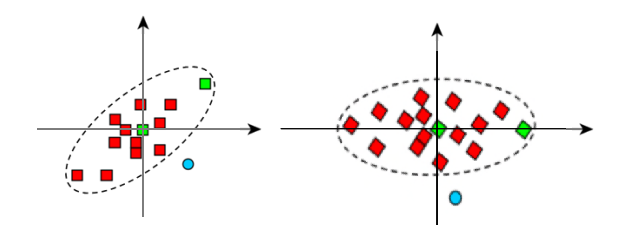
这样只是直观上看的更方便了，但仍然没有改变蓝绿两点与中心点的欧式距离。

这时细心的你肯定又观察出了端倪，数据在横向的方差比较大，而在纵向的方差比较小，这会造成量纲的不统一，所以我们还要对数据标准化（即让数据变成一个均值为 0 ，方差为 1 的分布）。
这里是有两个维度的，所以要对x,y两个方向都进行标准化。

$$x_{new}=\frac{x-\mu }{\sigma }$$

其中μ是样本均值，σ是样本数据的标准差。

这里我随机做了些数据

x = [0,-3,-3,-2,-2,-2,-1,-1,-1,-1,0,0,1,1,2,2,2,3]
y = [-1.5,-0.5,0.4,-0.5,-1,0.2,0.1,0,-1,0.5,1.2,-0.5,0.8,0.5,0,-0.5,0.5,0]

可视化出来如图：

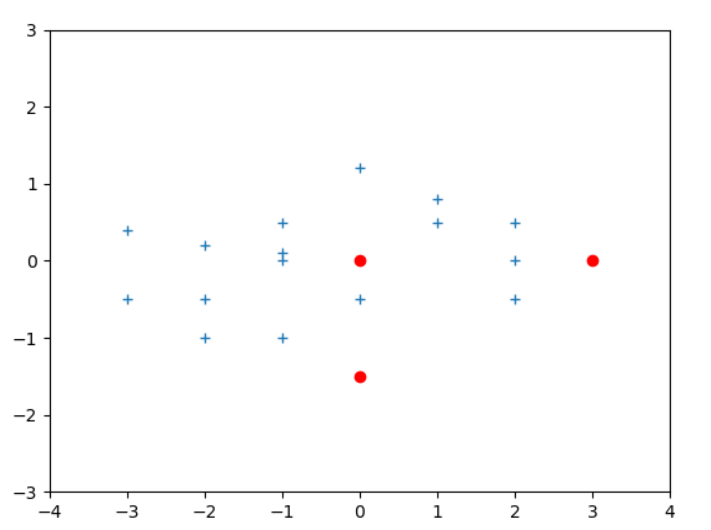
可以看到$(0,-1.5)$和$(3,0)$的距离，直观感觉$(3,0)$距离远点较远，是离群点。但再看看数据分布情况，在x轴上方差较大，y轴上方差较小，对齐标准化后再看看：

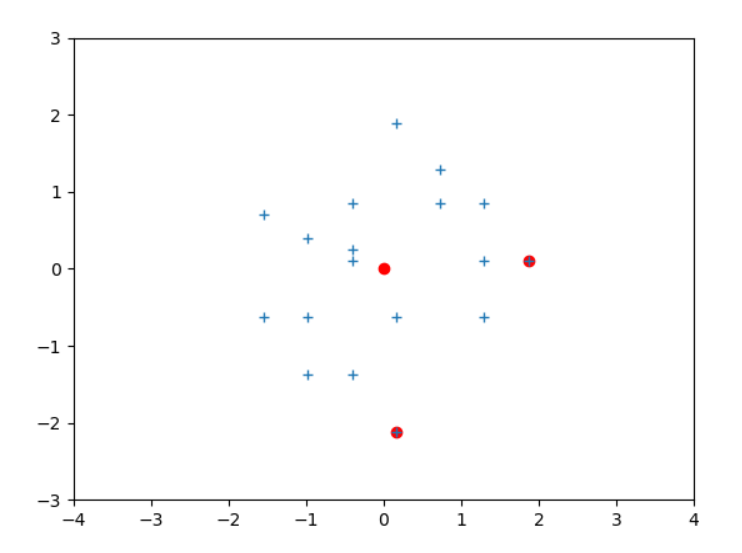
同样的坐标系，经标准化缩放后 原$(0,3)$点距离原点较近。

import numpy as np
import matplotlib.pyplot as plt
x = [0,-3,-3,-2,-2,-2,-1,-1,-1,-1,0,0,1,1,2,2,2,3]
y = [-1.5,-0.5,0.4,-0.5,-1,0.2,0.1,0,-1,0.5,1.2,-0.5,0.8,0.5,0,-0.5,0.5,0]x = np.array(x)
y = np.array(y)
plt.plot(x,y,'+')
plt.plot(0,0,'ro')
plt.plot(x[0],y[0],'ro')
plt.plot(x[-1],y[-1],'ro')
plt.xlim(-4,4)
plt.ylim(-3,3)
plt.show()a = np.mean(x)
b = np.mean(y)print(np.mean(x-a), np.mean(y-b))
print(np.std(x), np.std(y))x1 = (x-a)/np.std(x)
y1 = (y-b)/np.std(y)print(x1)
print(y1)
plt.plot(x1[0],y1[0],'ro')
plt.plot(x1[-1],y1[-1],'ro')
plt.xlim(-4,4)
plt.ylim(-3,3)
plt.plot(x1,y1,'+')
plt.plot(0,0,'ro')
plt.xlim(-4,4)
plt.ylim(-3,3)
plt.show()

由PCA这篇文章我们知道：设$C$为$X$的协方差矩阵，设 $Y$ 为 $X$ 对 $P$ 做基变换后的数据矩阵，即 $Y=PX$，注$P$是正交矩阵 。上面进行的基变换就是 $Y=PX$ 的过程。变换后有了Y，再求Y的欧氏距离就是所谓的马氏距离。

那如何将上面的过程就进行一个统一的结合呢？

设 $Y$ 的协方差矩阵为 D，则：
$$\begin{array}{lll}D& =& \frac{1}{m}Y{Y}^{\mathsf{T}}\\ & =& \frac{1}{m}(PX)(PX{)}^{\mathsf{T}}\\ & =& \frac{1}{m}PX{X}^{\mathsf{T}}{P}^{\mathsf{T}}\\ & =& P(\frac{1}{m}X{X}^{\mathsf{T}})P^{\mathsf{T}}\\ & =& PC{P}^{\mathsf{T}}\end{array}$$

由PCA我们知道，经变换后的 $X$ 在新的向量空间中是不相关的（正交的），所以D为对角阵。由于$X$已知，所以其协方差矩阵 $C$ 也就知道了，那如何找到 P对X进行变换呢？

由于$C$是一个是对称矩阵，在线性代数上，实对称矩阵有一系列非常好的性质：

1. 实对称矩阵不同特征值对应的特征向量必然正交。
2. 设特征向量 $\lambda$ 重数为 r，则必然存在 r 个线性无关的特征向量对应于 $\lambda$，因此可以将这 r 个特征向量单位正交化。

由上面两条可知，一个 n 行 n 列的实对称矩阵一定可以找到 n 个单位正交特征向量，设这 n 个特征向量为$e_1,e_2,\cdots ,e_n$，我们将其按列组成矩阵：
$$E=\left(\begin{array}{cccc}{e}_1& e_2& \cdots & e_n\end{array}\right)$$
则对协方差矩阵 C 有如下结论：
$$E^{\mathsf{T}}CE=\Lambda =\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right)$$

其中$\Lambda$ 为对角矩阵，其对角元素为各特征向量对应的特征值（可能有重复）。

以上结论不再给出严格的数学证明，对证明感兴趣的朋友可以参考线性代数书籍关于 “实对称矩阵对角化” 的内容。

到这里，我们发现我们已经找到了需要的矩阵 P：

$$P=E^{\mathsf{T}}$$

P 是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是 C 的一个特征向量。如果设 P 按照$\Lambda$ 中特征值的从大到小，将特征向量从上到下排列，则用P的前K行组成的矩阵乘以原始数据矩阵X，就得到了我们需要的降维后的数据矩阵Y。

以上不知道咋推了，于是有了以下

原文地址：www.cnblogs.com

马氏距离（Mahalanobis Distance）

马氏距离 (Mahalanobis Distance) 是由印度统计学家马哈拉诺比斯（P. C. Mahalanobis）提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。它考虑到数据特征之间的联系，并且是尺度无关的（scale-invariant），即独立于测量尺度。

马氏距离的定义

假设 $x$，$y$是从均值向量为$\mu$，协方差矩阵为$\Sigma$的总体 $G$中随机抽取的两个样本，定义 $x$，$y$两点之间的马氏距离为：

$$d_m^2(x,y)=(x-y{)}^T{\Sigma }^{-1}(x-y)$$

定义 $x$与总体 $G$的马氏距离为：

$$d_m^2(x,{\mu }_G)=(x-{\mu }_G{)}^T{\Sigma }^{-1}(x-{\mu }_G)$$

其中，如果协方差矩阵是单位向量，也就是各维度独立同分布，马氏距离就变成了欧氏距离。

注：上面的两个表达式其实是马氏距离的平方

为什么定义马氏距离

1. 数据指标的单位对距离度量的影响

在很多机器学习问题中，样本间的特征都可以用距离去描述，比如说最常见的欧氏距离。对于欧氏距离而言，空间中任意两点 $P=(x_1,x_2,\dots ,x_p)$与 $Q=(y_1,y_2,\dots ,y_p)$之间的距离为：

$$d(P,Q)=\sqrt{(x_1-y_1{)}^2+(x_2-y_2{)}^2+\cdots +(x_p-y_p{)}^2}$$

显然，当固定点 $Q$且取值为 $0$时，表示点 $P$到坐标原点的距离。

欧氏距离有一个缺点，就是当各个分量为不同性质的量时 (比如，人的身高与体重，西瓜的重量与体积)，“距离” 的大小竟然与指标的单位有关。例如，横轴 $x_1$代表重量（以 $kg$为单位），纵轴 $x_2$代表长度（以 $cm$为单位）。有四个点 $A,B,C,D$，如图 2.1 所示。

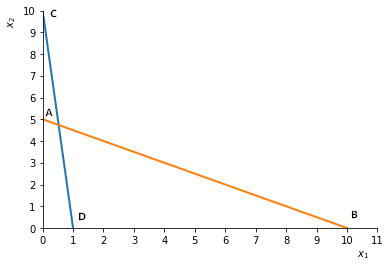
图 2.1

这时

$d(A,B)=\sqrt{5^2+10^2}=\sqrt{125}$
$d(C,D)=\sqrt{10^2+1^2}=\sqrt{101}$

显然，$AB$比 $CD$要长。

现在，如果 $x_2$用毫米 $(mm)$做单位，$x_1$保持不变，此时 $A$坐标 $(0,50)$，$C$坐标为 $(0,100)$，则

$d(A,B)=\sqrt{50^2+10^2}=\sqrt{2600}$
$d(C,D)=\sqrt{100^2+1^2}=\sqrt{10001}$

结果 $CD$反而比 $AB$长！这显然是不够合理的。

2. 样本分布对距离度量的影响

虽然我们可以先做归一化来消除这种维度间度量单位不同的问题，但是样本分布也会影响距离度量。我们可以看到，欧氏距离中每个坐标的权重是同等的。但是现实问题中，当坐标轴表示观测值时，它们往往带有大小不等的随机波动，即具有不同的方差，显然它们之间的权重是不同的。

下面举两个一维的例子说明这个问题：

设有两个正态分布总体 $G_1:N({\mu }_1,{\sigma }_1^2)$和 $G_2:N({\mu }_2,{\sigma }_2^2)$。若有一个样本，其值在点 A 处，那么，A 距离哪个总体近些呢？如图 2.2 所示：

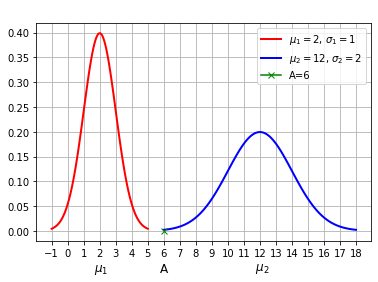
图 2.2

从绝对长度来看，点 A 距离左面的总体 $G_1$近些，即点 A 到${\mu }_1$比到${\mu }_2$要近些，（这里用的是欧氏距离，比较的是 A 点坐标与${\mu }_1$到${\mu }_2$值之差的绝对值），但从概率观点来看，A 点在${\mu }_1$右侧约 4${\sigma }_1$处，而在${\mu }_2$的左侧约 3${\sigma }_2$处，若以标准差来衡量，A 点距离${\mu }_2$要更 “近一些”。后者是从概率角度来考虑的，它是用坐标差的平方除以方差（或者说乘以方差的倒数），从而化为无量纲数，推广到多维就要乘以协方差矩阵$\Sigma$的逆矩阵${\Sigma }^{-1}$。

再来看下图 2.3，A 与 B 相对于原点的距离是相同的。但是由于样本总体沿着横轴分布，所以 B 点更有可能是这个样本中的点，而 A 则更有可能是离群点。在一个方差较小的维度下很小的差别就有可能成为离群点。

图 2.3

3. 维度间具有相关性对距离度量的影响

我们看到，上面描述的情形是维度间或者说特征之间是不相关的，那么如果维度间具有相关性会怎样呢？如下图 2.4 所示：

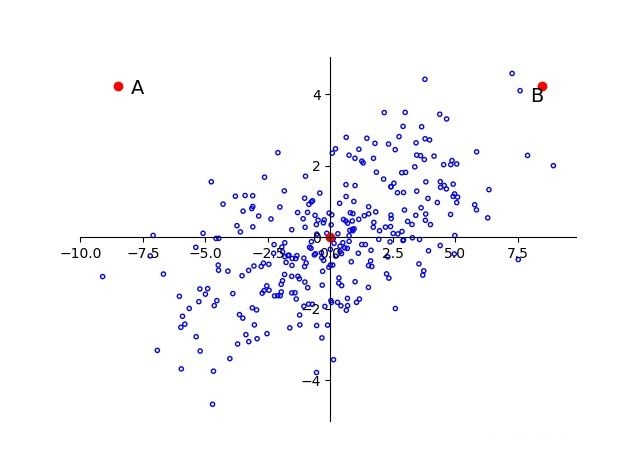
图 2.4

可以看到样本点可以近似看做是 $f(x)=x$的线性分布，A 与 B 相对于原点的距离依旧相等，显然 A 更像是一个离群点，也即是说离样本总体较远。

即使数据已经经过了标准化，也不会改变 AB 与原点间距离大小的相互关系。所以要本质上解决这个问题，就要针对主成分分析中的主成分来进行标准化。

为什么标准化不会改变距离大小的相互关系，这里以最常见的 z-score 标准化 (也叫标准差标准化）为例进行简单说明。这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为 0，标准差为 1，其转化函数为：$x^{\ast }=(x-\mu )/\sigma$，其中$\mu$为所有样本数据的均值，$\sigma$为所有样本数据的标准差。

显然这里的$\mu$和$\sigma$都是相同的，所以标准化只相当于对 A、B 点与数据中心距离进行了一个等比例缩放，并不影响它们之间大小的相互关系。
由此可见，仅仅靠标准化的欧氏距离还是存在很大问题的，数据相关性对判定结果的影响还是很大的。

为什么 z-score 标准化后的数据标准差为 1?

x-μ只改变均值，标准差不变，所以均值变为 0
(x-μ)/σ只会使标准差除以σ倍，所以标准差变为 1
即
$E(x^{\ast })=E[\frac{x-E(x)}{\sqrt{D(x)}}]=\frac{1}{\sqrt{D(x)}}E[x-E(x)]=0$

$D(x^{\ast })=D\left[\frac{x-E(x)}{\sqrt{D(x)}}\right]=\frac{1}{D(x)}D[x-E(x)]=\frac{D(x)}{D(x)}=1$

OK! 总结一下问题：

1）要考虑维度间相关性的影响
2）要考虑方差的影响
3）要考虑度量单位或者说量纲的影响

因此，有必要建立一种统计距离（只是一种术语，用于区别常用的欧氏距离），这种距离要能够体现各个变量在变差大小上的不同，以及有时存在着的相关性，还要求距离与各变量所用的单位无关。看来我们选择的距离要依赖于样本的方差和协方差。马氏距离就是最常用的一种统计距离。

马氏距离的几何意义

那么怎么办？，其实如果上面内容已经搞懂了，我们就会知道，只需要将变量按照主成分进行旋转，让维度间相互独立，然后进行标准化，让维度同分布就 OK 了，然后计算马氏距离就变成了计算欧氏距离。

由主成分分析可知，由于主成分就是特征向量方向，每个方向的方差就是对应的特征值，所以只需要按照特征向量的方向旋转，然后缩放特征值倍就可以了，可以得到以下的结果，图 2.5：

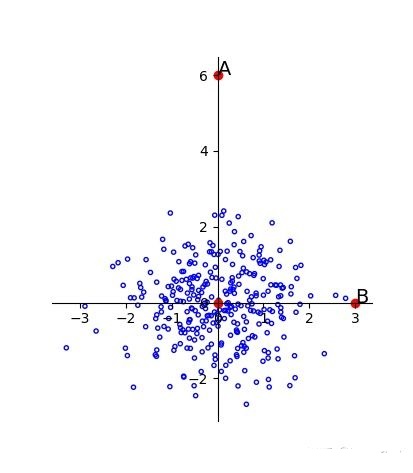
图 2.5

离群点就被成功分离，这时候的马氏距离就是欧氏距离。

马氏距离的推导

假设原始的多维样本数据 $X_{n\times m}$（$n$行，$m$列）：

$$X_{n\times m}=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1m}\\ x_{21}& x_{22}& \cdots & x_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{nm}\end{array}\right]$$

其中每行表示一个样本，$X_i$表示样本的第 $i$个维度，$X_i=(x_{1i},x_{2i},\dots ,x_{ni}{)}^T,i=1,2,\dots ,m$，则以上多维样本数据可记为：$X=(X_1,X_2,\dots ,X_m)$

样本总体的均值向量记为：${\mu }_X=({\mu }_{X1},{\mu }_{X2},\dots ,{\mu }_{Xm})$

协方差矩阵记为：${\Sigma }_X=E[(X-{\mu }_X{)}^T(X-{\mu }_X)]=\frac{1}{n}(X-{\mu }_X{)}^T(X-{\mu }_X)$

按照之前的描述，首先要对数据进行转换，旋转至主成分，使维度间线性无关。假设将原始数据 $X$通过坐标旋转矩阵 $U$变换得到了新的坐标，对应的新数据集记为 $F$（实际上 $X$，$F$表示的是同一个数据集，只是由于坐标值不同，为了区分而使用不同标记），数据集 $F$的均值向量记为${\mu }_F=({\mu }_{F1},{\mu }_{F2},\dots ,{\mu }_{Fm})$，则：

$$F^T=(F_1,F_2,\dots ,F_m)=U{X}^T$$

$$(F-{\mu }_F{)}^T=U(X-{\mu }_X{)}^T$$

$$(F-{\mu }_F)=(X-{\mu }_X)U^T$$

变换后的数据维度间线性无关，且每个维度的方差为特征值，即协方差矩阵${\Sigma }_F$是对角阵，所以：

$$\begin{array}{rl}{\Sigma }_F& =E[(F-{\mu }_F{)}^T(F-{\mu }_F)]\\ & =\frac{1}{n}(F-{\mu }_F{)}^T(F-{\mu }_F)\\ & =\frac{1}{n}U(X-{\mu }_X{)}^T(X-{\mu }_X)U^T\\ & =U{\Sigma }_X{U}^T\\ & =\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_m\end{array}\right)\end{array}$$

其中，${\lambda }_i,i=1,2,\dots ,m$表示每个维度的方差。

推导到这里之后，我们就可以推导出马氏距离公式了，假设要计算 $X$的一个样本点 $x=(x_1,x_2,\dots ,x_3)$到重心${\mu }_X=({\mu }_{X1},{\mu }_{X2},\dots ,{\mu }_{Xm})$的马氏距离。等价于求 $F$中点 $f=(f_1,f_2,\dots ,f_m)$标准化后的坐标值到标准化数据重心坐标值${\mu }_F=({\mu }_{F1},{\mu }_{F2},\dots ,{\mu }_{Fm})$的欧氏距离。

$$\begin{array}{rl}{d}_m^2(f,{\mu }_F)& =(\frac{f_1-{\mu }_{F1}}{\sqrt{{\lambda }_1}}{)}^2+(\frac{f_2-{\mu }_{F2}}{\sqrt{{\lambda }_2}}{)}^2+\cdots +(\frac{f_m-{\mu }_{Fm}}{\sqrt{{\lambda }_m}}{)}^2\\ & =(f_1-{\mu }_{F1},f_2-{\mu }_{F2},\dots ,f_m-{\mu }_{Fm})\left(\begin{array}{cccc}\frac{1}{{\lambda }_1}& & & \\ & \frac{1}{{\lambda }_2}& & \\ & & \ddots & \\ & & & \frac{1}{{\lambda }_m}\end{array}\right)\left(\begin{array}{c}{f}_1-{\mu }_{F1}\\ f_2-{\mu }_{F2}\\ ⋮\\ f_m-{\mu }_{Fm}\end{array}\right)\\ & =(f-{\mu }_F)(U{\Sigma }_X{U}^T{)}^{-1}(f-{\mu }_F{)}^T\\ & =(x-{\mu }_X)U^T(U{\Sigma }_X{U}^T{)}^{-1}U(x-{\mu }_X{)}^T\\ & =(x-{\mu }_X)U^T(U^T{)}^{-1}{\Sigma }_X^{-1}{U}^{-1}U(x-{\mu }_X{)}^T\\ & =(x-{\mu }_X){\Sigma }_X^{-1}(x-{\mu }_X{)}^T\end{array}$$

这就是前面定义的马氏距离的计算公式

如果 $x$是列向量，则

$$d_m^2(f,{\mu }_F)=(x-{\mu }_X{)}^T{\Sigma }_X^{-1}(x-{\mu }_X)$$

如果把推导过程中的重心点${\mu }_X$改换成任意其他样本点 $y$，则可以得到两个样本点之间的马氏距离公式为：

$$d_m^2(x,y)=(x-y{)}^T{\Sigma }_X^{-1}(x-y)$$

假设 $E$表示一个点集，$d$表示距离，它是 $E\times E$到 $[0,\infty )$的函数，可以证明，马氏距离符合距离度量的基本性质

以上！

机器学习笔记 - 距离度量与相似度
1）机器学习笔记 - 距离度量与相似度 (一) 闵可夫斯基距离

参考来源：
1）https://www.jianshu.com/p/5706a108a0c6
2）https://blog.csdn.net/u010167269/article/details/51627338
3）https://zhuanlan.zhihu.com/p/46626607
4）多元统计分析 - 何晓群

真想骂一下csdn，找了半天都看不懂，就在博客园看了这一篇就理解了。。。
说到底是自己菜！