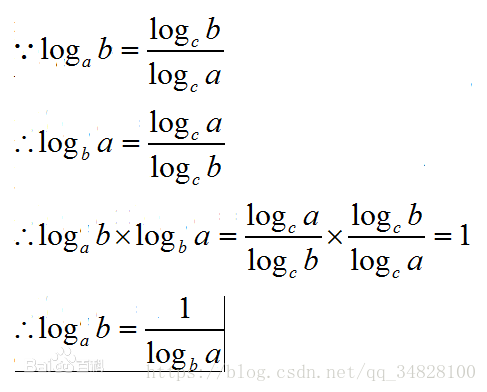对数函数与幂函数

news/2024/11/22 22:19:40/

对数函数

1. 金字塔

1.1 横线思考

  • 对数函数与指数函数的关系，互为反函数的关系；
  • 专业术语：底数、对数、真数（幂）、
  • 特殊对数函数：常数对数函数、自然对数函数；
  • 底数的取值范围：大于0，但是不等于1；
  • 对数函数的定义域 ： ( 0 &lt; x &lt; ∞ ) (0&lt;x&lt;\infty) (0<x<∞)
  • 对数函数的值域： ( − ∞ &lt; y &lt; ∞ ) (-\infty &lt; y &lt; \infty) (−∞<y<∞)

1.2 纵向思考

  • 对数函数的定义
  • 对数函数的性质
  • 对数函数的运算
  • 对数函数的图像

2.麦笔记

2.1 对数函数的定义

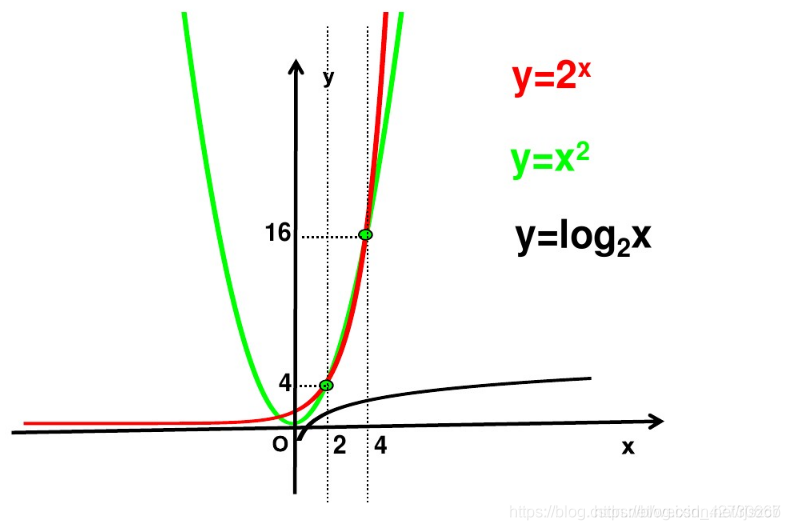
对数函数是指数函数的反函数，从定义的角度，可以从指数函数的反函数的角度进行考虑，对数函数与指数函数的图像关于 y = x y=x y=x对称，负数和零没有对数；

2.3 对数函数的运算

  • 如果 a &gt; 0 , 且 a ≠ 0 , M &gt; 0 , N &gt; 0 a&gt;0, 且a \neq 0, M &gt; 0, N &gt;0 a>0,且a̸​=0,M>0,N>0

( 1 ) log ⁡ a ( M ∗ N ) = log ⁡ a M + log ⁡ a N ; (1) \log_a{(M*N)}=\log_aM + \log_aN; (1)loga​(M∗N)=loga​M+loga​N;
( 2 ) log ⁡ a ( M N ) = log ⁡ a M − log ⁡ a N (2) \log_a{(\frac{M}{N} )} = \log_aM- \log_aN (2)loga​(NM​)=loga​M−loga​N
( 3 ) log ⁡ a M N = N log ⁡ a M ( N ϵ R ) (3) \log_a{M^N}=N\log_aM (N \epsilon R) (3)loga​MN=Nloga​M(NϵR)

  • 可以查询常数对数表、自然对数表。所以 下面介绍换底公式。

换 底 公 式 ： log ⁡ a b = log ⁡ c b log ⁡ c a 换底公式：\log_ab = {\frac{\log_cb}{\log_ca}} 换底公式：loga​b=logc​alogc​b​

2.4 对数函数的性质与图像

enter image description here

  • 定义域： ( 0 , + ∞ ) (0, +\infty) (0,+∞)
  • 值域： R R R
  • 性质：
    • （1）过定点(1,0)；
    • （2）当 a &gt; 1 时 a&gt;1时 a>1时，是增函数；
    • （3）当 0 &lt; a &lt; 1 时 0&lt;a&lt;1时 0<a<1时，是减函数；

幂函数

enter image description here


http://www.ppmy.cn/news/887346.html

相关文章

python对数函数如何表示

python对数函数如何表示

math.log(x) 就相当于数学中的ln(x)&#xff0c;x>0&#xff0c;求底数为e的对数&#xff0c;e 2.718281828459&#xff1b;math.log10(x) 就相当于数学中的lg(x)&#xff0c;x>0&#xff0c;求底数为10的对数。可以通过log(x[, base])来设置底数&#xff0c;如 log(x, …
阅读更多...
python中对数函数怎么表示

python中对数函数怎么表示

转载自品略图书馆 http://www.pinlue.com/article/2020/04/1007/4010139997805.html math.log(x) 就相当于数学中的ln(x)&#xff0c;x>0&#xff0c;求底数为e的对数&#xff0c;e 2.718281828459&#xff1b;math.log10(x) 就相当于数学中的lg(x)&#xff0c;x>0&…
阅读更多...
对数函数及运算

对数函数及运算

一般地&#xff0c;对数函数以 幂&#xff08; 真数&#xff09;为 自变量&#xff0c;指数为 因变量&#xff0c;底数为 常量的函数。 对数函数是6类 基本初等函数之一。其中 对数的定义&#xff1a; 如果a xN&#xff08;a>0&#xff0c;且a≠1&#xff09;&#xff0c;那…
阅读更多...
c++对数函数 log() 操作

c++对数函数 log() 操作

首先要知道exp&#xff08;&#xff09;函数 exp&#xff08;n&#xff09;值为e^n次方&#xff1b; 另外log函数包括两种函数 一种以e为低的log&#xff08;&#xff09;函数 另一种为以10为底的log 10&#xff08;&#xff09;函数&#xff1b; 具体用法见下面这个小程序…
阅读更多...
对数公式

对数公式

对数公式是数学中的一种常见公式&#xff0c;如果a^xN(a>0,且a≠1)&#xff0c;则x叫做以a为底N的对数,记做xlog(a)(N)&#xff0c;其中a要写于log右下。其中a叫做对数的底&#xff0c;N叫做真数。通常我们将以10为底的对数叫做常用对数&#xff0c;以e为底的对数称为自然对…
阅读更多...
指数函数，幂函数，对数函数

指数函数，幂函数，对数函数

摘自&#xff1a;https://zhikunhuo.blog.csdn.net/article/details/100828713 指数函数&#xff0c;幂函数&#xff0c;对数函数为高等数学中的初等函数 指数函数 指数函数公式为ya^{x}&#xff0c;其函数增长性如下&#xff1a; 指数函数的单调性是递增的&#xff0c;当x0…
阅读更多...
C++对数函数log()用法

C++对数函数log()用法

原文地址&#xff1a;https://blog.csdn.net/qq_40788630/article/details/79673539 首先要知道exp&#xff08;&#xff09;函数 exp&#xff08;n&#xff09;值为e^n次方&#xff1b; 另外log函数包括两种函数 一种以e为低的log&#xff08;&#xff09;函数 另一种为以…
阅读更多...
c语言对数函数log的使用

c语言对数函数log的使用

c语言log函数使用&#xff1a; #include<stdio.h> #include<math.h> int main(){ printf("%f\n",log(10)); //以e为底的对数函数 printf("%f\n",log10(100)); //以10为底的对数函数 printf("%f\n",log(8)/log(2)); //计算log2^8,运用…
阅读更多...
最新文章

Copyright @ 2022~2023