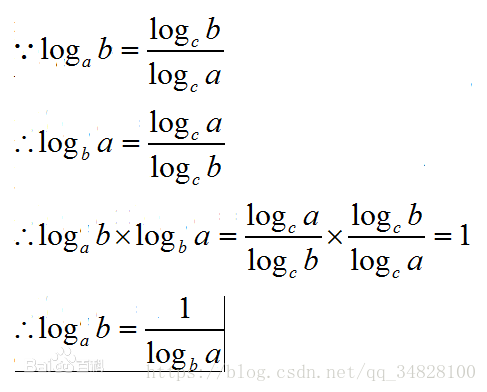首先要知道exp（）函数

exp（n）值为e^n次方；

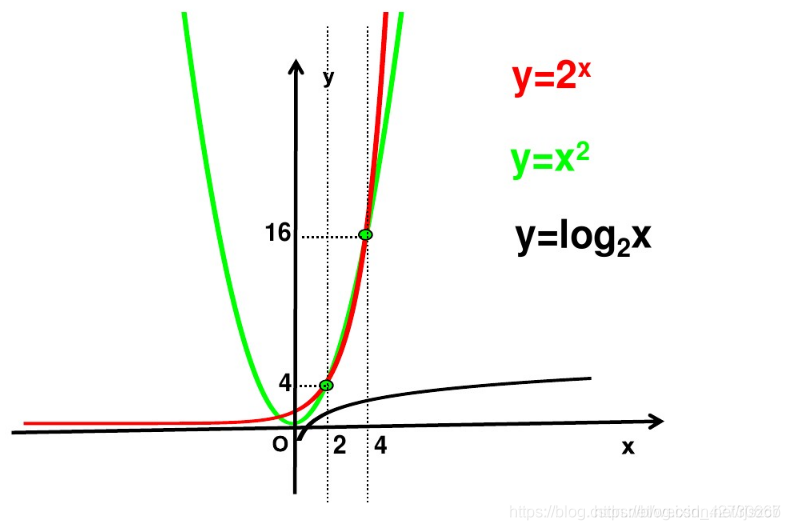
另外log函数包括两种函数 一种以e为低的log（）函数

另一种为以10为底的log 10（）函数；

具体用法见下面这个小程序

#include<iostream>
#include<cmath>
using namespace std;
int main()
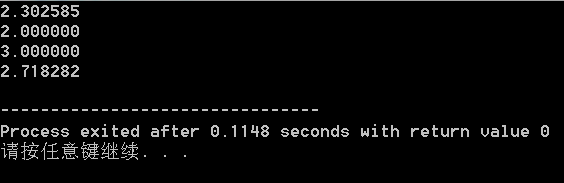
{double a=9,b=10;cout<<log(a)<<endl;cout<<log(exp(a))<<endl;cout<<log10(b)<<endl;return 0;
}

另外如果自定义以m为底，求log n的值

需要double a=log(n)/log(m);

举例如下：

#include<iostream>
#include<cmath>
using namespace std;
int main()
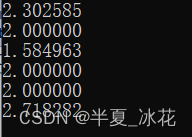
{double a=2,b=2;//以2为底的对数函数 for(b=2;b<=16;b=b+2){cout<<"b="<<b<<"时，以2为底的对数函数="<<log(b)/log(a)<<endl;}return 0;
}