摘自：https://zhikunhuo.blog.csdn.net/article/details/100828713

指数函数，幂函数，对数函数为高等数学中的初等函数

指数函数
指数函数公式为y=a^{x}，其函数增长性如下：

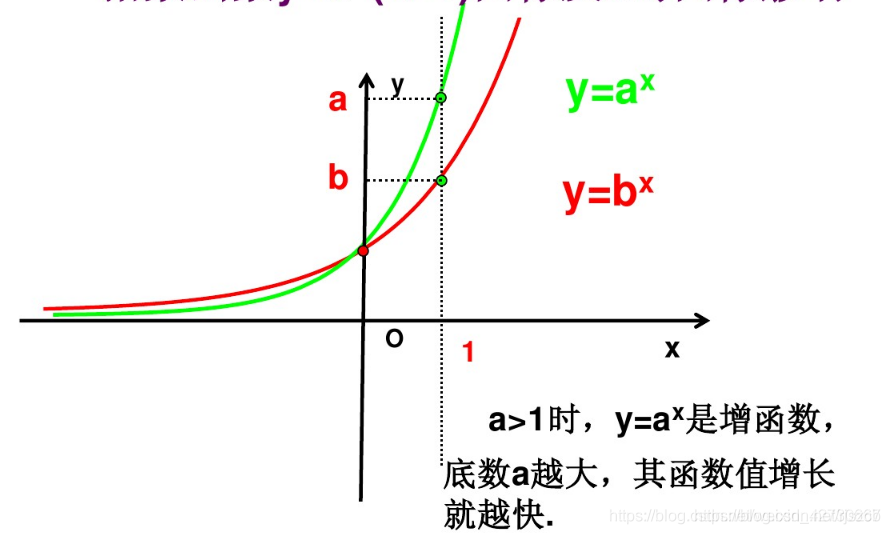
指数函数的单调性是递增的，当x=0时，不管a为任何值，其值为1。当a大于1时，随着a越大，其函数值增长越快

在x>0部分，a>b其y值也是随着f_{a}(x)>f_{b}(x)

在x<0部分 当a>b是，其f_{a}(x)<f_{b}(x)<1

对数函数
对数函数表达式为：y=log_{a}x,其函数图像为如下：

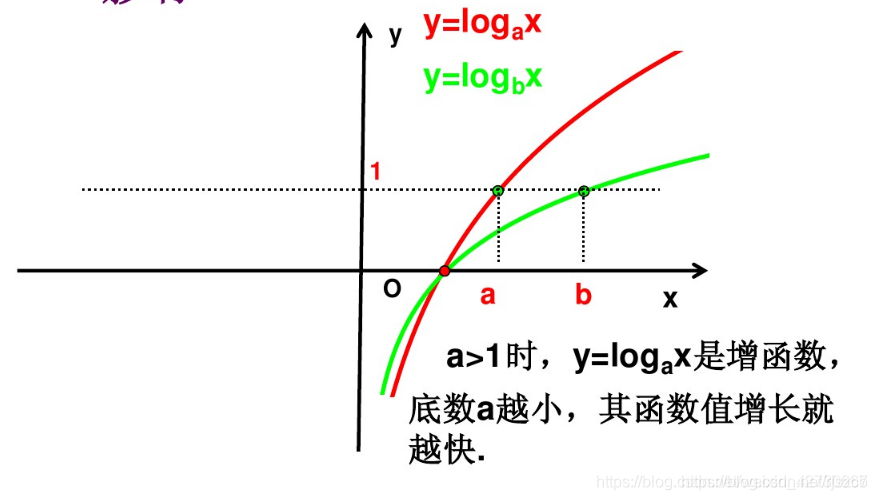
当x等于1时 y为0，

当x<1时，其y值小于0

当x >1时，其值大于0

对数函数为单调递增的，当a>1时，随着地鼠a越小，其函数增长值越快

当x> 1时， a<b，f_{a}(x)>f_{b}(x)

当x<1时， a<b ,f_{a}(x)<f_{b}(x)

幂函数
幂函数表达式为y=x^{n},其图像如图：

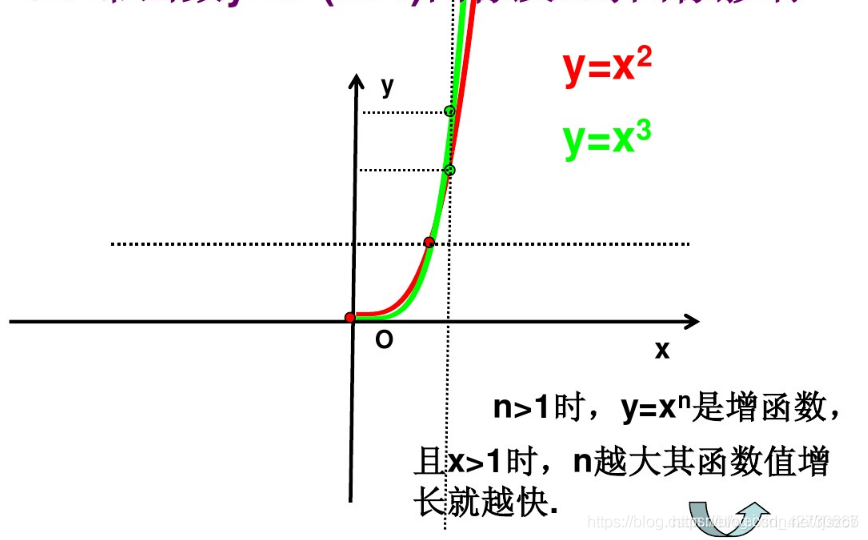
对数函数为单调递增的，当n大于1时且x大于1时， n越大其函数值越大

比较三个函数y=2^{x},y=x{2},y=log_{2}x增长快慢

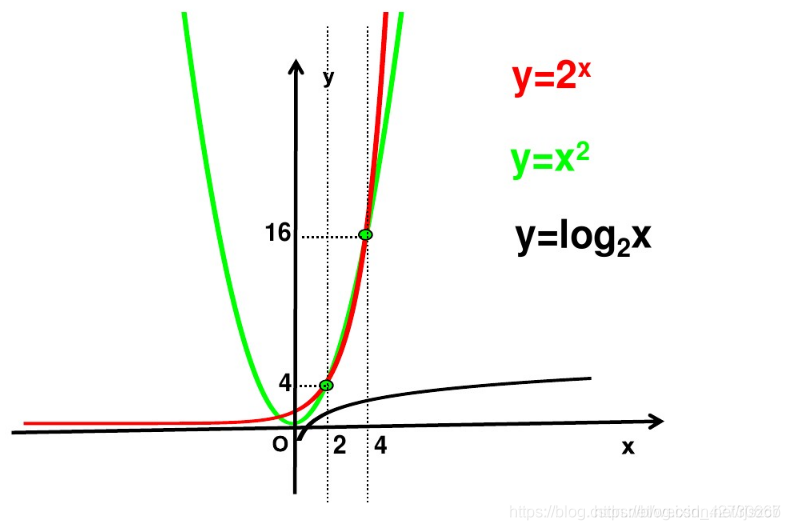
y=log_{2}x增长最慢，幂函数y=x^{{2}和指数函数y=2}{x}快慢交替进行

在x(0.2)区间,幂函数比指函数增长较快

在（4，+\propto）指数函数比幂函数增长较快