张量场
张量场表示张量 T ( x ⃗ , t ) T(\vec x, t) T(x,t)在空间 x ⃗ \vec x x和时间 t t t中如何变化,将张量场视为可微函数
如果一个张量场不依赖于时间,则此张量场称为定常场,例如 T = T ( x ⃗ ) T = T(\vec x) T=T(x);相反,如果一个张量场只依赖时间则称为均匀场,就是说 T ( t ) T(t) T(t)在每个位置 x ⃗ \vec x x都有相同的值
张量场可以分类为:标量、向量、二阶张量场等
例如温度场 T ( x ⃗ , t ) T(\vec x, t) T(x,t) 就是一个标量场,在时间 t = t 1 t = t_1 t=t1中温度的分布如下:
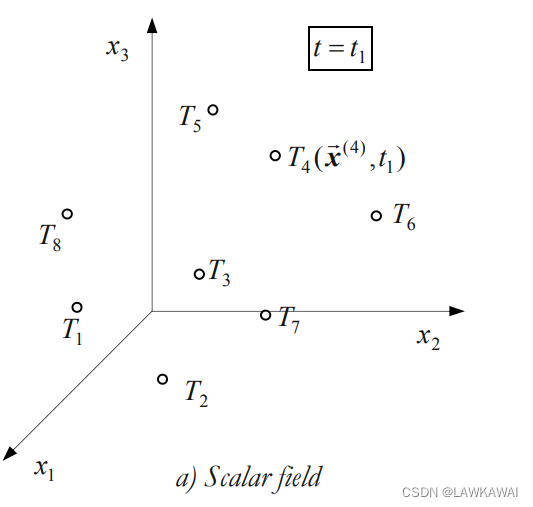
另外,速度场 v ⃗ ( x ⃗ , t ) \vec v(\vec x, t) v(x,t)是一个向量场,在时间 t = t 1 t = t_1 t=t1的速度分布,在每一个点都有一个速度相对应,如下所示:
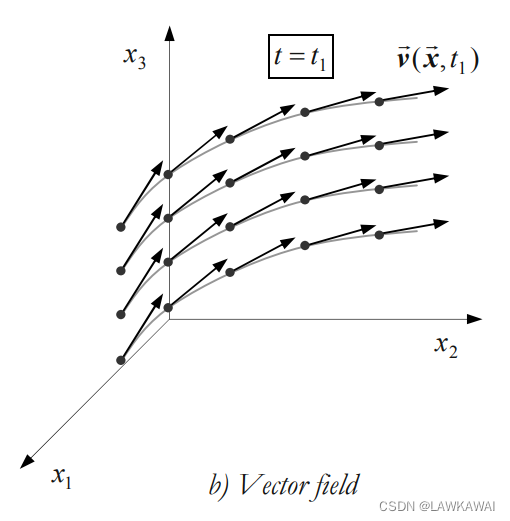
标量场:
ϕ = ϕ ( x ⃗ , t ) \phi=\phi(\vec x, t) ϕ=ϕ(x,t)
向量场:
张量表示: v ⃗ = v ⃗ ( x ⃗ , t ) \vec v = \vec v (\vec x, t) v=v(x,t)
下标表示: v i = v i ( x ⃗ , t ) v_i = v_i(\vec x, t) vi=vi(x,t)
二阶张量场:
张量表示: T = T ( x ⃗ , t ) T=T (\vec x, t) T=T(x,t)
下标表示: T i j = T i j ( x ⃗ , t ) T_{ij}= T_{ij}(\vec x, t) Tij=Tij(x,t)
标量场
定常标量场 ϕ = ϕ ( x ⃗ ) \phi = \phi(\vec x) ϕ=ϕ(x),有连续的值 ∂ ϕ ∂ x 1 , ∂ ϕ ∂ x 2 , ∂ ϕ ∂ x 3 \frac{\partial \phi}{\partial x_1}, \frac{\partial \phi}{\partial x_2}, \frac{\partial \phi}{\partial x_3} ∂x1∂ϕ,∂x2∂ϕ,∂x3∂ϕ。在点 x ⃗ \vec x x的函数值为 ϕ ( x ⃗ ) \phi(\vec x) ϕ(x),在另一个点 x ⃗ + d x ⃗ \vec x + d\vec x x+dx的函数值为 ϕ ( x ⃗ + d x ⃗ ) \phi(\vec x + d\vec x) ϕ(x+dx),那么函数 ϕ \phi ϕ的微分定义如下:
ϕ ( x ⃗ + d x ⃗ ) − ϕ ( x ⃗ ) ≡ d ϕ ϕ ( x 1 + d x 1 , x 2 + d x 2 , x 3 + d x 3 ) − ϕ ( x 1 , x 2 , x 3 ) ≡ d ϕ \phi(\vec x + d\vec x)-\phi(\vec x)\equiv d\phi\\ \phi(x_1+dx_1, x_2+dx_2, x_3+dx_3)-\phi(x_1, x_2, x_3)\equiv d\phi ϕ(x+dx)−ϕ(x)≡dϕϕ(x1+dx1,x2+dx2,x3+dx3)−ϕ(x1,x2,x3)≡dϕ
对于任意的连续函数 ϕ ( x 1 , x 2 , x 3 ) \phi(x_1, x_2, x_3) ϕ(x1,x2,x3), d ϕ d\phi dϕ 与 d x 1 , d x 2 , d x 3 dx_1, dx_2, dx_3 dx1,dx2,dx3线性相关,这种线性关系可以以微分的链式法则来给出:
d ϕ = ∂ ϕ ∂ x 1 d x 1 + ∂ ϕ ∂ x 2 d x 2 + ∂ ϕ ∂ x 3 d x 3 d\phi = \frac{\partial \phi}{\partial x_1}dx_1+\frac{\partial \phi}{\partial x_2}dx_2+\frac{\partial \phi}{\partial x_3}dx_3 dϕ=∂x1∂ϕdx1+∂x2∂ϕdx2+∂x3∂ϕdx3
张量的分量关于 x i x_i xi的导数,可以由以下微分算子表示:
∂ ∗ ∂ x i ≡ ∗ , i \frac{\partial \ast}{\partial x_i}\equiv \ast_{,i} ∂xi∂∗≡∗,i
梯度
标量场的梯度:
梯度 ∇ x ⃗ ϕ \nabla_{\vec x}\phi ∇xϕ 或者 g r a d ϕ grad \phi gradϕ定义为:
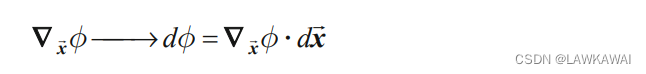
其中,算子 ∇ x ⃗ \nabla_{\vec x} ∇x叫Nabla符号,将上式表示成笛卡尔坐标基:
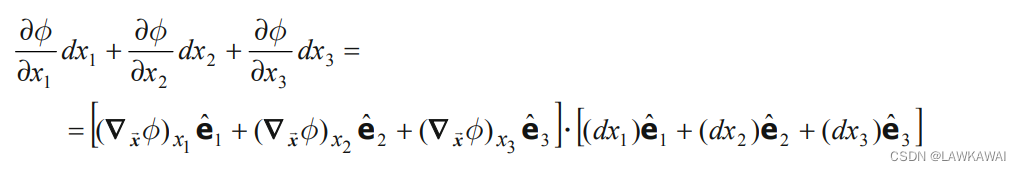
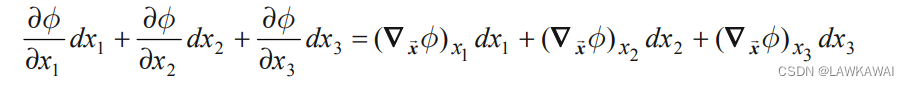
所以, ∇ x ⃗ ϕ \nabla_{\vec x}\phi ∇xϕ在笛卡尔坐标系中的分量:
( ∇ x ⃗ ) 1 ≡ ∂ ϕ ∂ x 1 ; ( ∇ x ⃗ ) 2 ≡ ∂ ϕ ∂ x 2 ; ( ∇ x ⃗ ) 3 ≡ ∂ ϕ ∂ x 3 ; (\nabla_{\vec x})_1 \equiv \frac{\partial \phi}{\partial x_1}; \quad (\nabla_{\vec x})_2 \equiv \frac{\partial \phi}{\partial x_2}; \quad (\nabla_{\vec x})_3 \equiv \frac{\partial \phi}{\partial x_3}; \quad (∇x)1≡∂x1∂ϕ;(∇x)2≡∂x2∂ϕ;(∇x)3≡∂x3∂ϕ;
那么,梯度的分量定义如下:
∇ x ⃗ ϕ = ∂ ϕ ∂ x 1 e ^ 1 + ∂ ϕ ∂ x 2 e ^ 2 + ∂ ϕ ∂ x 3 e ^ 3 \nabla_{\vec x}\phi=\frac{\partial \phi}{\partial x_1}\hat e_1+\frac{\partial \phi}{\partial x_2}\hat e_2+\frac{\partial \phi}{\partial x_3}\hat e_3 ∇xϕ=∂x1∂ϕe^1+∂x2∂ϕe^2+∂x3∂ϕe^3
Nabla符号 ∇ x ⃗ \nabla_{\vec x} ∇x定义为:
∇ x ⃗ = ∂ ∂ x i e ^ i ≡ ∂ , i e ^ i \boxed{\nabla_{\vec x}=\frac{\partial }{\partial x_i}\hat e_i\equiv \partial_{,i}\hat e_i} ∇x=∂xi∂e^i≡∂,ie^i
∇ , x ⃗ \nabla_{,\vec x} ∇,x的几何意义:
- ∇ x ⃗ \nabla_{\vec x} ∇x的方向是垂直于等值面的,例如垂直于等值面 ϕ = c o n s t \phi = const ϕ=const。 ∇ x ⃗ \nabla_{\vec x} ∇x的方向指向 ϕ \phi ϕ增长最快的方向
- ∇ x ⃗ \nabla_{\vec x} ∇x的大小是 ϕ \phi ϕ改变的速率,例如 ϕ \phi ϕ的梯度
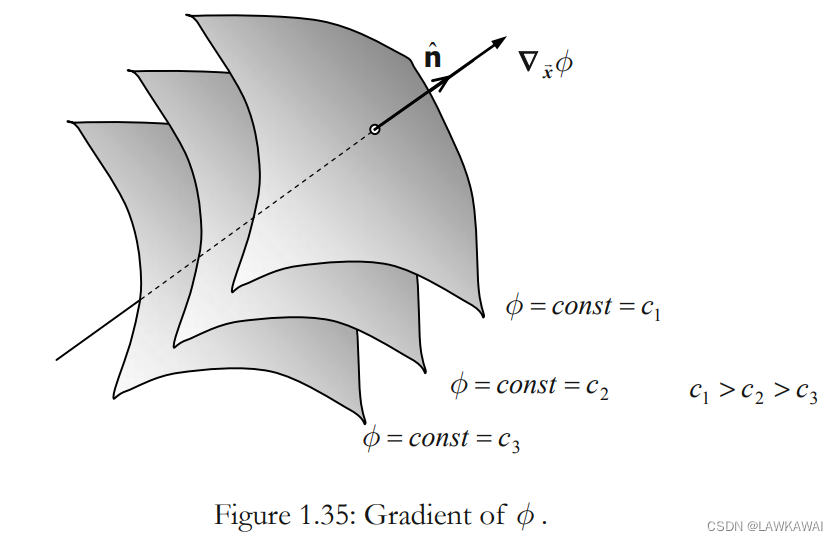
一个曲面的法向量如下所示:
n ^ = ∇ x ⃗ ϕ ∣ ∣ ∇ x ⃗ ϕ ∣ ∣ \hat n = \frac{\nabla_{\vec x}\phi}{||\nabla_{\vec x}\phi||} n^=∣∣∇xϕ∣∣∇xϕ
曲面 ϕ = c o n s t \phi = const ϕ=const,为等值面,在所有的点上都有相同的值,所以在等值面上移动函数值不发生改变
向量场 v ⃗ ( x ⃗ ) \vec v (\vec x) v(x)的梯度:
g r a d ( v ⃗ ) ≡ ∇ x ⃗ v ⃗ grad(\vec v)\equiv\nabla_{\vec x}\vec v grad(v)≡∇xv
表示成:
∇ x ⃗ v ⃗ = ∂ v i e ^ i ∂ x j ⨂ e ^ j = ( v i e ^ i ) , j ⨂ e ^ j = v i , j e ^ i ⨂ e ^ j \nabla_{\vec x}\vec v=\frac{\partial v_i \hat e_i}{\partial x_j}\bigotimes \hat e_j=(v_i \hat e_i)_{,j}\bigotimes \hat e_j=v_{i,j}\hat e_i \bigotimes \hat e_j ∇xv=∂xj∂vie^i⨂e^j=(vie^i),j⨂e^j=vi,je^i⨂e^j
因此,可以在笛卡尔坐标系中定义一个张量场 ( ∗ ( x ⃗ , t ) ) (*(\vec x, t)) (∗(x,t))的梯度为:
∇ x ⃗ ( ∗ ) = ∂ ∗ ∂ x j ⨂ e ^ j ( 在笛卡尔坐标系中的张量场的梯度 ) \boxed{\nabla_{\vec x}(*)=\frac{\partial *}{\partial x_j}\bigotimes \hat e_j}(在笛卡尔坐标系中的张量场的梯度) ∇x(∗)=∂xj∂∗⨂e^j(在笛卡尔坐标系中的张量场的梯度)
二阶张量场的梯度:
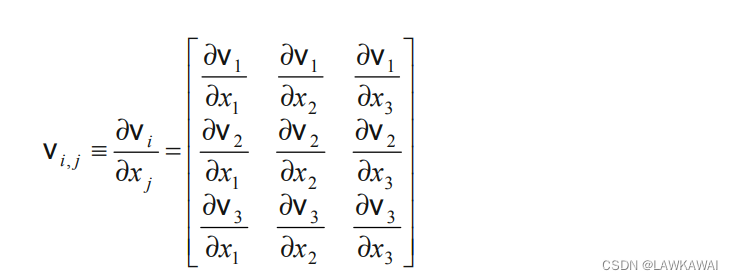
二阶张量场 T ( x ⃗ ) T(\vec x) T(x)的梯度:
∇ x ⃗ T = ∂ T i j e ^ i ⨂ e ^ j ∂ x k ⨂ e ^ k = T i j , k e ^ i ⨂ e ^ j ⨂ e ^ k \nabla_{\vec x}T = \frac{\partial T_{ij}\hat e_i \bigotimes \hat e_j}{\partial x_k}\bigotimes \hat e_k=T_{ij, k}\hat e_i\bigotimes \hat e_j \bigotimes \hat e_k ∇xT=∂xk∂Tije^i⨂e^j⨂e^k=Tij,ke^i⨂e^j⨂e^k
表示为:
( ∇ x ⃗ T ) i j k = T i j , k (\nabla_{\vec x}T)_{ijk}=T_{ij,k} (∇xT)ijk=Tij,k
问题1.41求出函数 f ( x 1 , x 2 ) = cos ( x 1 ) + exp x 1 x 2 f(x_1, x_2)=\cos(x_1)+\exp^{x_1x_2} f(x1,x2)=cos(x1)+expx1x2在点 ( x 1 = 0 , x 2 = 1 ) (x_1=0, x_2=1) (x1=0,x2=1) 的梯度

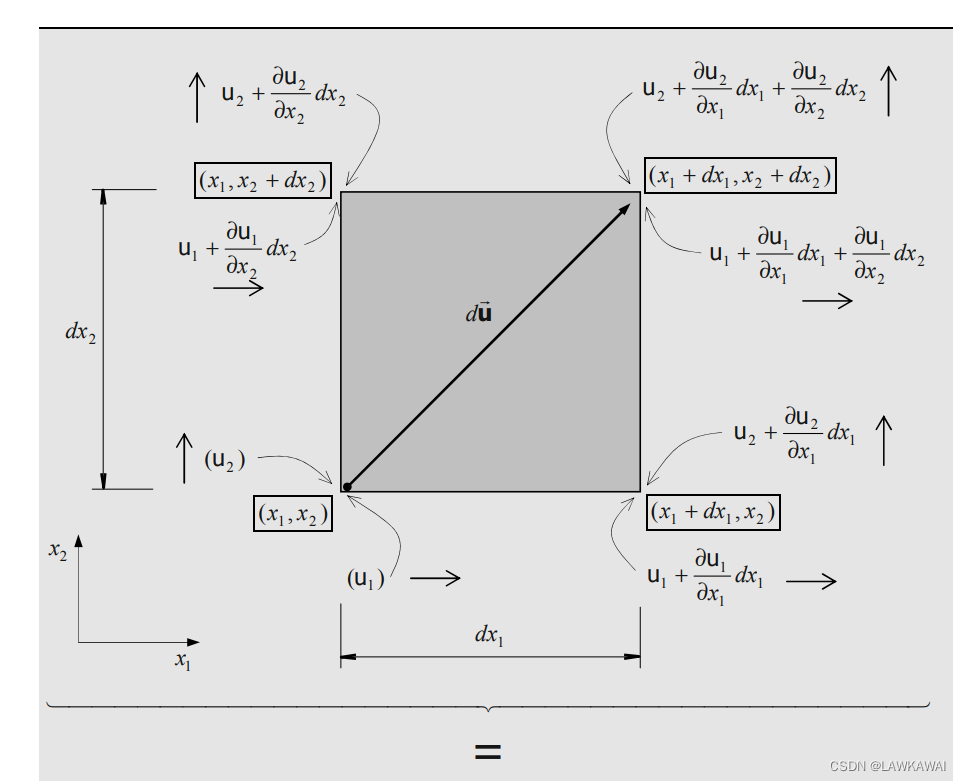
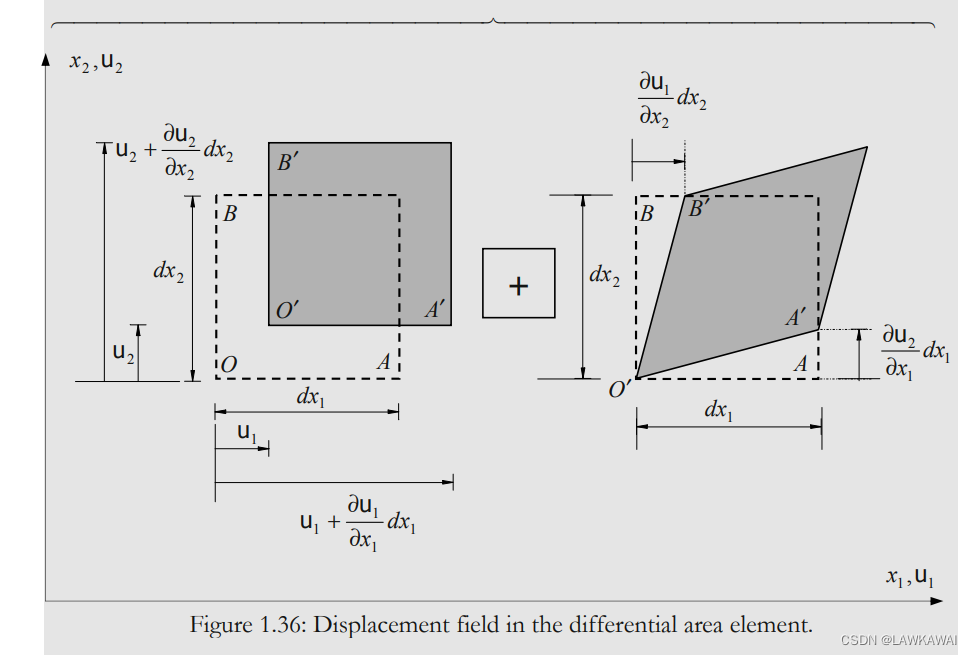
问题1.42 u ⃗ ( x ⃗ ) \vec u(\vec x) u(x)是一个定常场


散度
向量场 v ⃗ ( x ⃗ ) \vec v(\vec x) v(x)的散度,标记如下:
d i v ( v ⃗ ) ≡ ∇ x ⃗ ⋅ v ⃗ div(\vec v)\equiv \nabla_{\vec x}\cdot \vec v div(v)≡∇x⋅v
表示为:
d i v ( v ⃗ ) ≡ ∇ x ⃗ ⋅ v ⃗ = ∇ x ⃗ v ⃗ : 1 = T r ( ∇ x ⃗ v ⃗ ) div(\vec v)\equiv\nabla_{\vec x}\cdot \vec v=\nabla_{\vec x}\vec v:1=Tr(\nabla_{\vec x}\vec v) div(v)≡∇x⋅v=∇xv:1=Tr(∇xv)
那么:
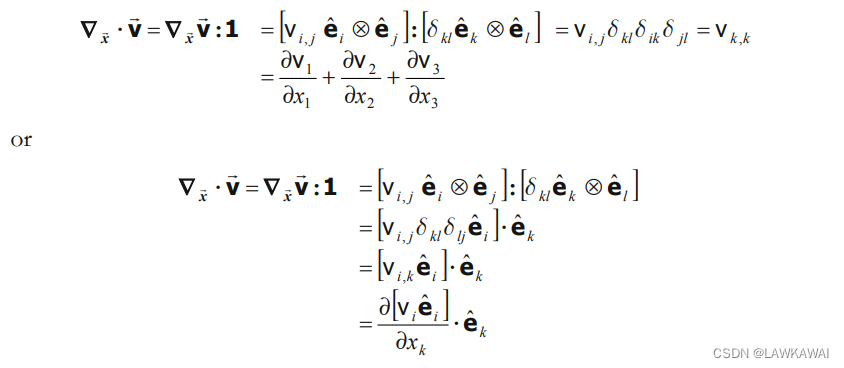
笛卡尔坐标系下的算子:
∇ x ⃗ ⋅ ( ∗ ) = ∂ ( ∗ ) ∂ x k ⋅ e ^ k ( 笛卡尔坐标系下 ( ∗ ) 的散度 ) \boxed{\nabla_{\vec x}\cdot (*)=\frac{\partial (*)}{\partial x_k}\cdot \hat e_k}(笛卡尔坐标系下(*)的散度) ∇x⋅(∗)=∂xk∂(∗)⋅e^k(笛卡尔坐标系下(∗)的散度)
可以验证,当张量场作用散度时,其秩降低一阶
二阶张量场 T ( x ⃗ ) T(\vec x) T(x)的散度:
二阶张量场 T T T的散度定义为 ∇ x ⃗ ⋅ 1 = ∇ x ⃗ T : 1 \nabla_{\vec x}\cdot 1=\nabla_{\vec x}T:1 ∇x⋅1=∇xT:1,得到一个向量:
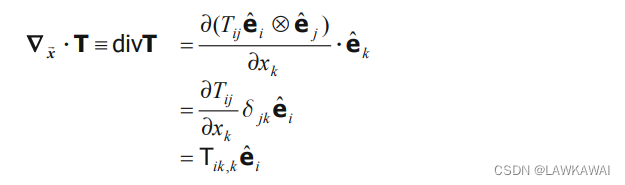
NOTE:注意了,在处理张量场的梯度和散度时,
例如 ∇ x ⃗ v ⃗ \nabla_{\vec x}\vec v ∇xv(向量场的梯度)、 ∇ x ⃗ T \nabla_{\vec x}T ∇xT(二阶张量场的梯度)、 ∇ x ⃗ ⋅ T \nabla_{\vec x}\cdot T ∇x⋅T(二阶张量场的散度),这不意味着在对向量和张量之间进行张量算子操作,
例如 ∇ x ⃗ v ⃗ ≠ ( ∇ ⃗ x ⃗ ) ⨂ v ⃗ \nabla_{\vec x}\vec v\neq ( \vec \nabla_{\vec x})\bigotimes \vec v ∇xv=(∇x)⨂v, ∇ x ⃗ T ≠ ( ∇ ⃗ x ⃗ ) ⨂ v ⃗ \nabla_{\vec x}T\neq (\vec \nabla_{\vec x})\bigotimes \vec v ∇xT=(∇x)⨂v以及 ∇ x ⃗ ⋅ T ≠ ( ∇ ⃗ x ⃗ ) ⋅ ( T ) \nabla_{\vec x}\cdot T \neq (\vec \nabla_{\vec x})\cdot (T) ∇x⋅T=(∇x)⋅(T),等
∇ x ⃗ \nabla_{\vec x} ∇x必须是一个作用在完整张量场的算子,所以张量必须在算子的内部
然而,可以有如下表示:

定义 拉普拉斯算子 ∇ 2 \nabla^2 ∇2 为:
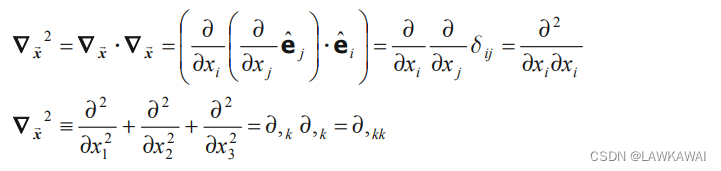
那么,向量场 v ⃗ \vec v v的拉普拉斯向量为:
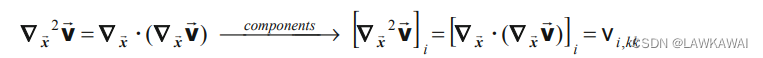
问题1.43 令 a ⃗ \vec a a和 b ⃗ \vec b b是向量,证明等式 ∇ x ⃗ ⋅ ( a ⃗ + b ⃗ ) = ∇ x ⃗ ⋅ a ⃗ + ∇ x ⃗ ⋅ b ⃗ \nabla_{\vec x}\cdot (\vec a + \vec b)=\nabla_{\vec x}\cdot \vec a+\nabla_{\vec x}\cdot \vec b ∇x⋅(a+b)=∇x⋅a+∇x⋅b成立

问题1.44 求出 ( ∇ x ⃗ a ⃗ ) ⋅ b ⃗ (\nabla_{\vec x}\vec a)\cdot \vec b (∇xa)⋅b
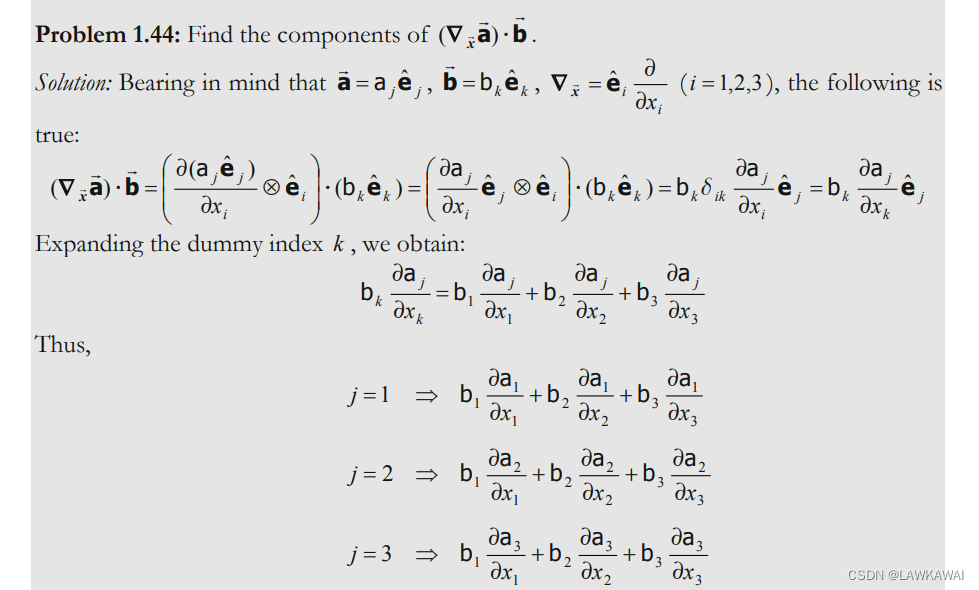
问题1.45 证明以下关系成立
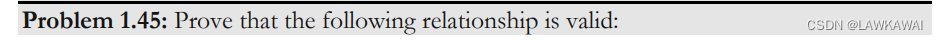

旋度
向量场的旋度:
向量场 v ⃗ ( x ⃗ ) \vec v(\vec x) v(x)的旋度: c u r l ( v ⃗ ) ≡ r o t ( v ⃗ ) ≡ ∇ x ⃗ ∧ v ⃗ curl(\vec v)\equiv rot(\vec v)\equiv \nabla_{\vec x} \wedge \vec v curl(v)≡rot(v)≡∇x∧v,并且用笛卡尔坐标基表示:
∇ ⃗ x ⃗ ∧ ( ∗ ) = ∂ ∂ x j e ^ j ∧ ( ∗ ) ( 在笛卡尔坐标系下的张量场的旋度 ) \boxed{\vec \nabla_{\vec x}\wedge (*)=\frac{\partial }{\partial x_j}\hat e_j \wedge (*)(在笛卡尔坐标系下的张量场的旋度)} ∇x∧(∗)=∂xj∂e^j∧(∗)(在笛卡尔坐标系下的张量场的旋度)
指标形式:
r o t ( v ⃗ ) = ∇ ⃗ x ⃗ ∧ v ⃗ = ∂ ∂ x j e ^ j ∧ v ⃗ k e ^ k = ∂ v k ∂ x j e ^ j ∧ e ^ k = ∂ v k ∂ x j ϵ i j k e ^ i = ϵ i j k v k , j e ^ i rot(\vec v)=\vec \nabla_{\vec x}\wedge \vec v=\frac{\partial }{\partial x_j}\hat e_j\wedge \vec v_k \hat e_k=\frac{\partial v_k}{\partial x_j}\hat e_j\wedge \hat e_k =\frac{\partial v_k}{\partial x_j}\epsilon_{ijk}\hat e_i=\epsilon_{ijk}v_{k,j}\hat e_i rot(v)=∇x∧v=∂xj∂e^j∧vke^k=∂xj∂vke^j∧e^k=∂xj∂vkϵijke^i=ϵijkvk,je^i
展开:
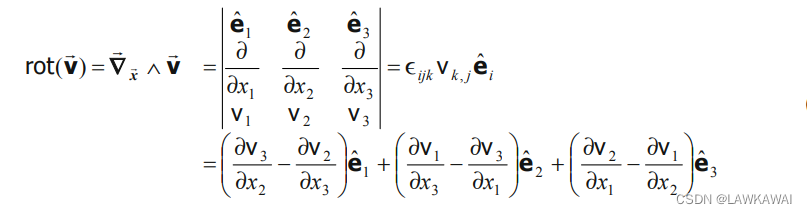
可以验证,一个向量场梯度的反对称部分,即 ( ∇ x ⃗ v ⃗ ) s k e w ≡ W (\nabla_{\vec x}\vec v)^{skew}\equiv W (∇xv)skew≡W,有如下分量:
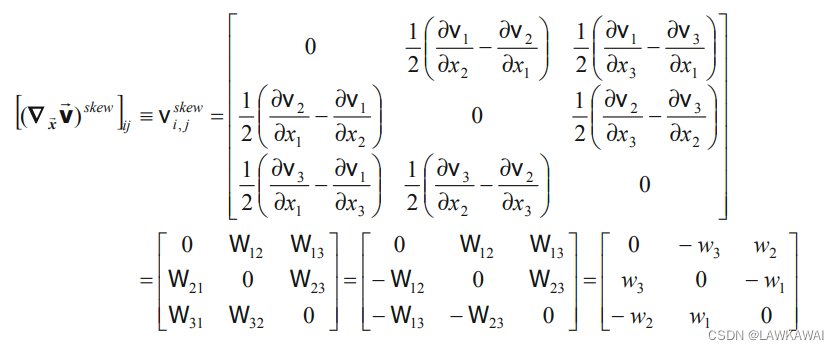
其中, w 1 , w 2 , w 3 w_1, w_2, w_3 w1,w2,w3是W的轴向量 w ⃗ \vec w w的分量
所以,结合旋度的定义和反对称矩阵分量,得到:
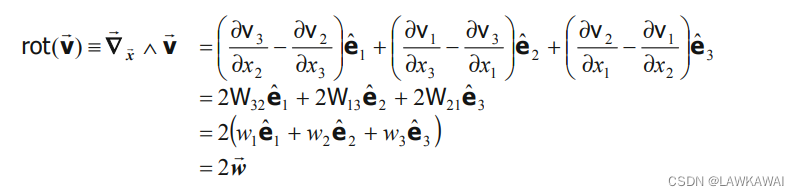
由于反对称张量和轴向量有以下关系:
W ⋅ a ⃗ = w ⃗ ∧ a ⃗ \boxed{W \cdot \vec a=\vec w \wedge \vec a} W⋅a=w∧a
所以:
W ⋅ v ⃗ = w ⃗ ∧ v ⃗ = 1 2 ( ∇ ⃗ x ⃗ ∧ v ⃗ ) ∧ v ⃗ W \cdot \vec v=\vec w \wedge \vec v=\frac{1}{2}(\vec \nabla_{\vec x} \wedge \vec v)\wedge \vec v W⋅v=w∧v=21(∇x∧v)∧v
我们在问题1.18里证明了反对称张量 ( x ⃗ ⨂ a ⃗ ) s k e w (\vec x \bigotimes \vec a)^{skew} (x⨂a)skew的轴向量是 1 2 ( a ⃗ ∧ x ⃗ ) \frac{1}{2}(\vec a \wedge \vec x) 21(a∧x),因此反对称张量 W = ( ∇ ⃗ x ⃗ v ⃗ ) s k e w = [ ( v ⃗ ) ⨂ ∇ ⃗ x ⃗ ] s k e w W = (\vec \nabla_{\vec x}\vec v)^{skew}=[(\vec v) \bigotimes \vec \nabla_{\vec x}]^{skew} W=(∇xv)skew=[(v)⨂∇x]skew的轴向量是 1 2 ( ∇ ⃗ x ⃗ ∧ v ⃗ ) \frac{1}{2}(\vec \nabla_{\vec x}\wedge \vec v) 21(∇x∧v)
如上所示,旋度描述了向量场的旋转趋势
总结:
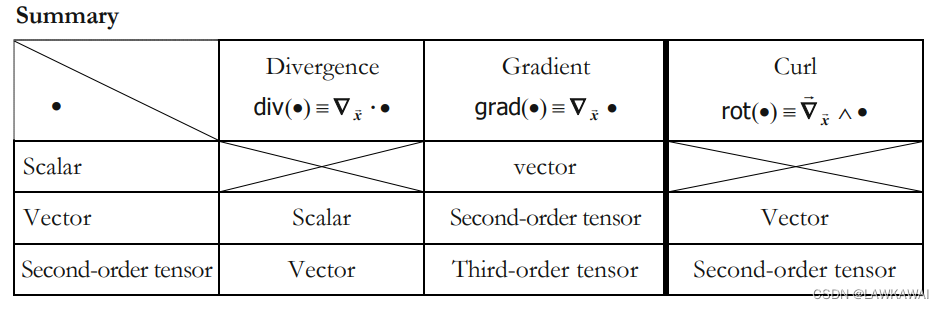
-
r o t ( λ a ⃗ ) = ∇ ⃗ x ⃗ ∧ ( λ a ⃗ ) = λ ( ∇ ⃗ x ⃗ ∧ a ⃗ ) + ( ∇ x ⃗ λ ∧ a ⃗ ) rot(\lambda \vec a)=\vec \nabla_{\vec x}\wedge (\lambda \vec a)=\lambda (\vec \nabla_{\vec x}\wedge \vec a)+( \nabla_{\vec x} \lambda \wedge \vec a) rot(λa)=∇x∧(λa)=λ(∇x∧a)+(∇xλ∧a)
∇ ⃗ x ⃗ ∧ ( λ a ⃗ ) \vec \nabla_{\vec x}\wedge (\lambda \vec a) ∇x∧(λa)的结果是一个向量,分量为:
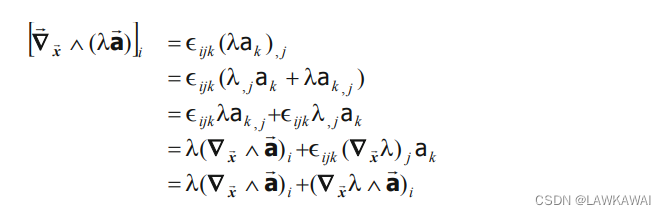
所以有: r o t ( λ a ⃗ ) = ∇ ⃗ x ⃗ ∧ ( λ a ⃗ ) = λ ( ∇ ⃗ x ⃗ ∧ a ⃗ ) + ( ∇ x ⃗ λ ∧ a ⃗ ) rot(\lambda \vec a)=\vec \nabla_{\vec x}\wedge (\lambda \vec a)=\lambda(\vec \nabla_{\vec x}\wedge \vec a)+(\nabla_{\vec x}\lambda \wedge \vec a) rot(λa)=∇x∧(λa)=λ(∇x∧a)+(∇xλ∧a) -
∇ ⃗ x ⃗ ∧ ( a ⃗ ∧ b ⃗ ) = ( ∇ x ⃗ ⋅ b ⃗ ) a ⃗ − ( ∇ a ⃗ ⋅ a ⃗ ) b ⃗ + ( ∇ x ⃗ a ⃗ ) ⋅ b ⃗ − ( ∇ x ⃗ b ⃗ ) ⋅ a ⃗ \vec \nabla_{\vec x}\wedge (\vec a \wedge \vec b)=(\nabla_{\vec x}\cdot \vec b)\vec a-(\nabla_{\vec a}\cdot \vec a)\vec b+(\nabla_{\vec x}\vec a)\cdot \vec b-(\nabla_{\vec x}\vec b)\cdot \vec a ∇x∧(a∧b)=(∇x⋅b)a−(∇a⋅a)b+(∇xa)⋅b−(∇xb)⋅a
由于有: ( a ⃗ ∧ b ⃗ ) = ϵ k i j a i b j (\vec a \wedge \vec b)=\epsilon_{kij}a_ib_j (a∧b)=ϵkijaibj,因此:
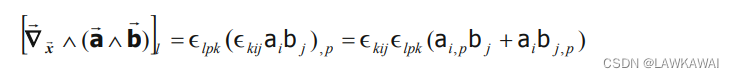
并且有: ϵ k i j = ϵ i j k \epsilon_{kij}=\epsilon_{ijk} ϵkij=ϵijk且 ϵ i j k ϵ l p k = δ i l δ j p − δ i p δ j l \epsilon_{ijk}\epsilon_{lpk}=\delta_{il}\delta_{jp}-\delta_{ip\delta_{jl}} ϵijkϵlpk=δilδjp−δipδjl,那么:
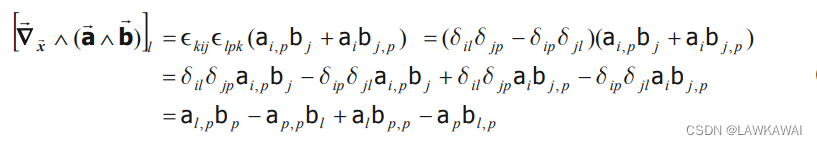
可以验证: [ ( ∇ x ⃗ a ⃗ ) ⋅ b ⃗ ] l = a l , p b p [(\nabla_{\vec x}\vec a)\cdot \vec b]_l=a_{l,p}b_p [(∇xa)⋅b]l=al,pbp, [ ( ∇ x ⃗ ⋅ a ⃗ ) b ⃗ ] l = a p , p b l [(\nabla_{\vec x}\cdot \vec a)\vec b]_l=a_{p,p}b_l [(∇x⋅a)b]l=ap,pbl, [ ( ∇ x ⃗ ⋅ b ⃗ ) a ⃗ ] l = a l b p , p [(\nabla_{\vec x}\cdot \vec b)\vec a]_l=a_lb_{p,p} [(∇x⋅b)a]l=albp,p, [ ( ∇ x ⃗ b ⃗ ) ⋅ a ⃗ ] l = a p b l , p [(\nabla_{\vec x} \vec b)\cdot \vec a]_l=a_pb_{l,p} [(∇xb)⋅a]l=apbl,p -
∇ ⃗ x ⃗ ∧ ( ∇ ⃗ x ⃗ ∧ a ⃗ ) = ∇ x ⃗ ( ∇ x ⃗ ⋅ a ⃗ ) − ∇ x ⃗ 2 a ⃗ \vec \nabla_{\vec x}\wedge (\vec \nabla_{\vec x}\wedge \vec a)=\nabla_{\vec x}(\nabla_{\vec x}\cdot \vec a)-\nabla_{\vec x}^2 \vec a ∇x∧(∇x∧a)=∇x(∇x⋅a)−∇x2a
由于: ( ∇ x ⃗ ∧ a ⃗ ) i = ϵ i j k a k , j (\nabla_{\vec x}\wedge \vec a)_i=\epsilon_{ijk}a_k,j (∇x∧a)i=ϵijkak,j,因此:
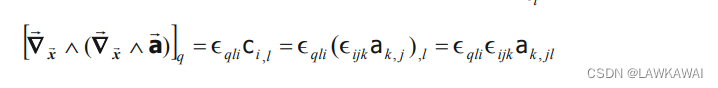
考虑: ϵ q l i ϵ i j k = ϵ q l i ϵ j k i = δ q j δ l k − δ q k δ l j \epsilon_{qli}\epsilon_{ijk}=\epsilon_{qli}\epsilon_{jki}=\delta_{qj}\delta_{lk}-\delta_{qk}\delta_{lj} ϵqliϵijk=ϵqliϵjki=δqjδlk−δqkδlj,有:
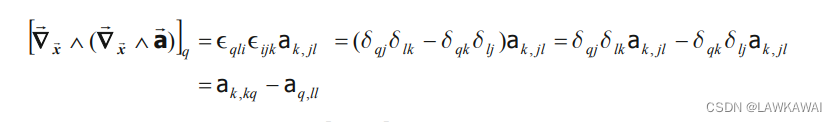
其中, [ ∇ x ⃗ ( ∇ x ⃗ ⋅ a ⃗ ) ] q = a k , k q [\nabla_{\vec x}(\nabla_{\vec x}\cdot \vec a)]_q=a_{k,kq} [∇x(∇x⋅a)]q=ak,kq和 [ ∇ x ⃗ 2 a ⃗ ] q = a q , l l [\nabla_{\vec x}^2\vec a]_q=a_{q,ll} [∇x2a]q=aq,ll -
∇ x ⃗ ⋅ ( ψ ∇ x ⃗ ⋅ a ⃗ ) = ψ ∇ x ⃗ 2 ϕ + ( ∇ x ⃗ ψ ) ⋅ ( ∇ x ⃗ ϕ ) \nabla_{\vec x} \cdot(\psi \nabla_{\vec x}\cdot \vec a)=\psi \nabla_{\vec x}^2\phi+(\nabla_{\vec x}\psi)\cdot (\nabla_{\vec x}\phi) ∇x⋅(ψ∇x⋅a)=ψ∇x2ϕ+(∇xψ)⋅(∇xϕ)

ψ \psi ψ和 ϕ \phi ϕ是标量场,以上等式由以下等式推导而来:
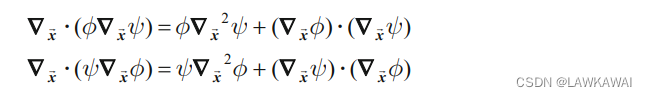
将两个等式相减,得:
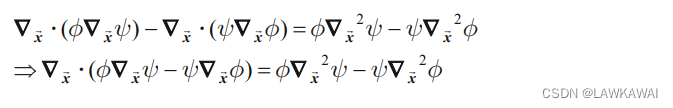
保守场
一个向量场 b ⃗ ( x ⃗ , t ) \vec b(\vec x, t) b(x,t)被称为保守的,如果存在一个可导的标量场 ϕ ( x ⃗ , t ) \phi(\vec x, t) ϕ(x,t),满足:
b ⃗ = ∇ x ⃗ ϕ \vec b = \nabla_{\vec x}\phi b=∇xϕ
如果一个函数 ϕ \phi ϕ满足以上关系,则称 ϕ \phi ϕ是 b ⃗ ( x ⃗ , t ) \vec b(\vec x, t) b(x,t)的势函数。
b ⃗ ( x ⃗ , t ) \vec b(\vec x, t) b(x,t)是保守的的一个不充分条件是 ∇ ⃗ x ⃗ ∧ b ⃗ = 0 ⃗ \vec \nabla_{\vec x}\wedge \vec b=\vec 0 ∇x∧b=0。也就是说,给定一个保守场,其旋度 ∇ ⃗ x ⃗ ∧ b ⃗ \vec \nabla_{\vec x}\wedge \vec b ∇x∧b等于0。反而,如果一个向量场的旋度为0,不代表这个向量场是保守的
1.46 ϕ \phi ϕ是一个标量场, u ⃗ \vec u u是一个向量场,证明 ∇ x ⃗ ⋅ ( ∇ x ⃗ ∧ v ⃗ ) = 0 \nabla_{\vec x}\cdot (\nabla_{\vec x}\wedge \vec v)=0 ∇x⋅(∇x∧v)=0以及 ∇ ⃗ x ⃗ ∧ ( ∇ x ⃗ ϕ ) = 0 ⃗ \vec \nabla_{\vec x}\wedge (\nabla_{\vec x}\phi)=\vec 0 ∇x∧(∇xϕ)=0


参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics