比赛记录:Codeforces Round 874 (Div. 3) A~G

传送门:CF

前题提要:赛时A出了5道题,并且都是一遍过的,F题也已经找到了解决方法,但是没时间完成了.以为应该能上分,但是没想到赛后E题被hack掉了…绝了.然后打完这场 $d i v 3$ 后立马阳了,加上一大堆烦心事(包括但不限于各类考试).就导致现在才写出这篇题解.

A题:A. Musical Puzzle

我们发现这道题就是求长度为2的不同的字符串的个数.因为只要有一种字符串我们合成了,那么对于接下来的合成来说,只要碰到该字符串,我们只要使用直接合成过的字符串即可

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int main() {int T=read();while(T--) {int n=read();map<string,int>mp;string s;cin>>s;int ans=0;for(int i=1;i<s.length();i++) {string ss;ss.push_back(s[i-1]);ss.push_back(s[i]);if(mp[ss]) {continue;}else {mp[ss]=1;ans++;}}cout<<ans<<endl;}return 0;
}

B题:B. Restore the Weather

有一说一这道题思维上还真有点难度.当时在赛场上把我卡了一下.感觉思维难度相当于 $d i v 2 B$ 了.
这道题的突破口在于猜想(bushi.毕竟是CF嘛,结论猜就完了.其实不难猜出应该a中越小的与b中越小的搭配应该是最优的.这个想证明也不难证.假设数列a中有 $A, B$ 两个元素,并且 $A < B$ .数列b中有 $C, D$ 两个元素,并且 $C, D$ ,我们发现总共只有下列几种情况:
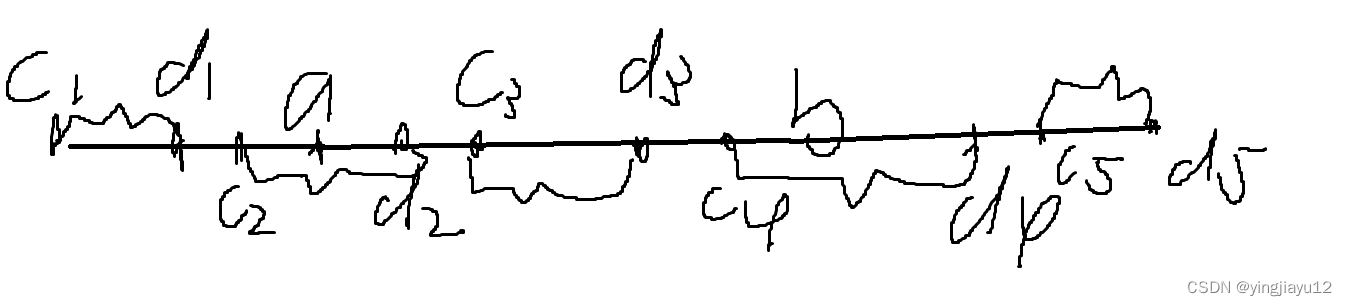
在这里插入图片描述
对于所有情况,我们都会发现 $m a x (a b s (A - C), a b s (B - D)) < m a x (a b s (A - D), a b s (B - C))$ .所以就是小的搭配小的是最优的.
所以我们计算出每一个元素在a数组中的排第几位,然后输出其在b数组中应该的位置即可.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int b[maxn];
struct Node{int num,id;bool operator < (const Node &rhs) const {return num<rhs.num;}
}a[maxn];
int paiming[maxn];
int main() {int T=read();while(T--) {int n=read();int k=read();vector<int>v;for(int i=1;i<=n;i++) {a[i].num=read();a[i].id=i;v.push_back(a[i].num);}sort(a+1,a+n+1);for(int i=1;i<=n;i++) {paiming[a[i].id]=i;b[i]=read();}sort(b+1,b+n+1);for(int i=1;i<=n;i++) {cout<<b[paiming[i]]<<" ";}cout<<endl;}return 0;
}

C题:C. Vlad Building Beautiful Array

感觉本题比B题要简单.看完题面,首先想到的想法应该是分类讨论.讨论最后的构造数组中应该全是奇数或者全是偶数.
对于全是偶数的情况,十分简单.对于每一个 $a_i$ ,假设当前数是偶数,那么显然我们可以直接选取,但是假设此时我们至少存在一个奇数.我们发现此时无论如何也无法构造出了.为什么呢,因为只要存在奇数,显然我们可以找到最小的那一个奇数,对于这个最小的奇数来说,我们没法找到比它更小的奇数了(因为它本身就是最小).所以此时无法构造.
对于全部都是奇数的情况.我们记录一下最小的那一个数.如果最小的那一个数是奇数的话,我们显然都是可行的.如果最小的那一个数是偶数的话,那么对于这个偶数来说,我们依旧无法将这个最小的偶数转化为奇数.

ps:关于本题的代码,我在写题解时突然发现之前赛时写的代码看似逻辑全无,但是仔细考虑了一下逻辑竟然又是正确的(毕竟赛时过了),难道这就是直觉吗…,所以我就把这个逻辑全无的代码放上来了,供大家把玩一下.经典的实现方式我相信在上述的讲解过程中已经不难写出了

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];
int main() {int T=read();while(T--) {int n=read();int minn1=int_INF;for(int i=1;i<=n;i++) {a[i]=read();minn1=min(minn1,a[i]);}int flag1=0;int flag2=0;for(int i=1;i<=n;i++) {if(a[i]%2==1) {continue;}else {if(minn1<a[i]) {continue;}else {flag1=1;break;}}}for(int i=1;i<=n;i++) {if(a[i]%2==1) {flag2=1;break;}else {continue;}}if(!(flag1&&flag2)) cout<<"YES"<<endl;else cout<<"NO"<<endl;}return 0;
}

D题:D. Flipper

对于我来说,本题唯一坑点是数字可能存在两位数,所以在实现过程中是不能用string来存储数字的
把玩一下题意不难发现无论第一位是什么数字,经过操作之后该位置的数字必定会被放到后面去.所以我们首先需要找到的是除第一位以外的最大的那一个数的位置(记为 $p o s$ ),那么显然的,我们此时需要将其放到第一位的位置上去.对比一下我们能进行的操作,我们发现我们的 $[p o s, n]$ 的所有数字都将放到首位.

然后我们需要考虑的是pos前面的数字是否在哪一处区间进行了翻转操作.诶此时我们显然可以枚举翻转区间的左端点,然后对于每一次枚举的操作,我们都将那个区间翻转然后在后面加上前缀,记录最大的字典序即可

此处需要注意的是当我们的最大值后缀的长度为1时,我们可以仅对该位置的数字进行翻转,这样就比上述的枚举方案多了一种情况了,这个需要注意.

对于枚举的时候如何方便的判断字典序的最大值.可以考虑使用vector.因为可能有多位数的原因,我们不能使用string了.注意vector也是可以翻转的.并且vector自身是重载了运算符的,也就是当两个vector进行比较时,就是以存的数字的字典序进行比较的.vector真是太优越啦

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int p[maxn];
int main() {int T=read();while(T--) {int n=read();for(int i=1;i<=n;i++) p[i]=read();if(n==1) {cout<<p[1]<<endl;continue;}int maxx=-int_INF;if(p[1]!=n) maxx=n;else maxx=n-1;int pos;for(int i=n;i>=2;i--) {if(p[i]==maxx) {pos=i;break;}}vector<int>ans;for(int i=pos;i<=n;i++) ans.push_back(p[i]);vector<int>v;for(int i=1;i<pos;i++) v.push_back(p[i]);vector<int>maxx2;int cnt=(pos==n?0:1);for(int i=v.size()-cnt;i>=0;i--) {vector<int>v2;for(int j=i;j<v.size();j++) {v2.push_back(v[j]);}reverse(v2.begin(),v2.end());vector<int>v3;for(int j=0;j<v2.size();j++) v3.push_back(v2[j]);for(int j=0;j<i;j++) {v3.push_back(v[j]);}maxx2=max(maxx2,v3);}for(int i=0;i<ans.size();i++) {cout<<ans[i]<<" ";}for(int i=0;i<maxx2.size();i++) {cout<<maxx2[i]<<" ";}cout<<endl;}
}

E题:E. Round Dance

这道题赛后被狠狠的hack掉了,真是醉了,只能怪这道题的赛时数据有点弱了,我被hack的那一种情况显然应该是存在的,但是测试点中并不存在.

看完题意之后不难发现应该是一道图论题.对于每一个数的邻居.考虑对他们俩连一条单向边.最后不难发现应该存在这样几种情况:
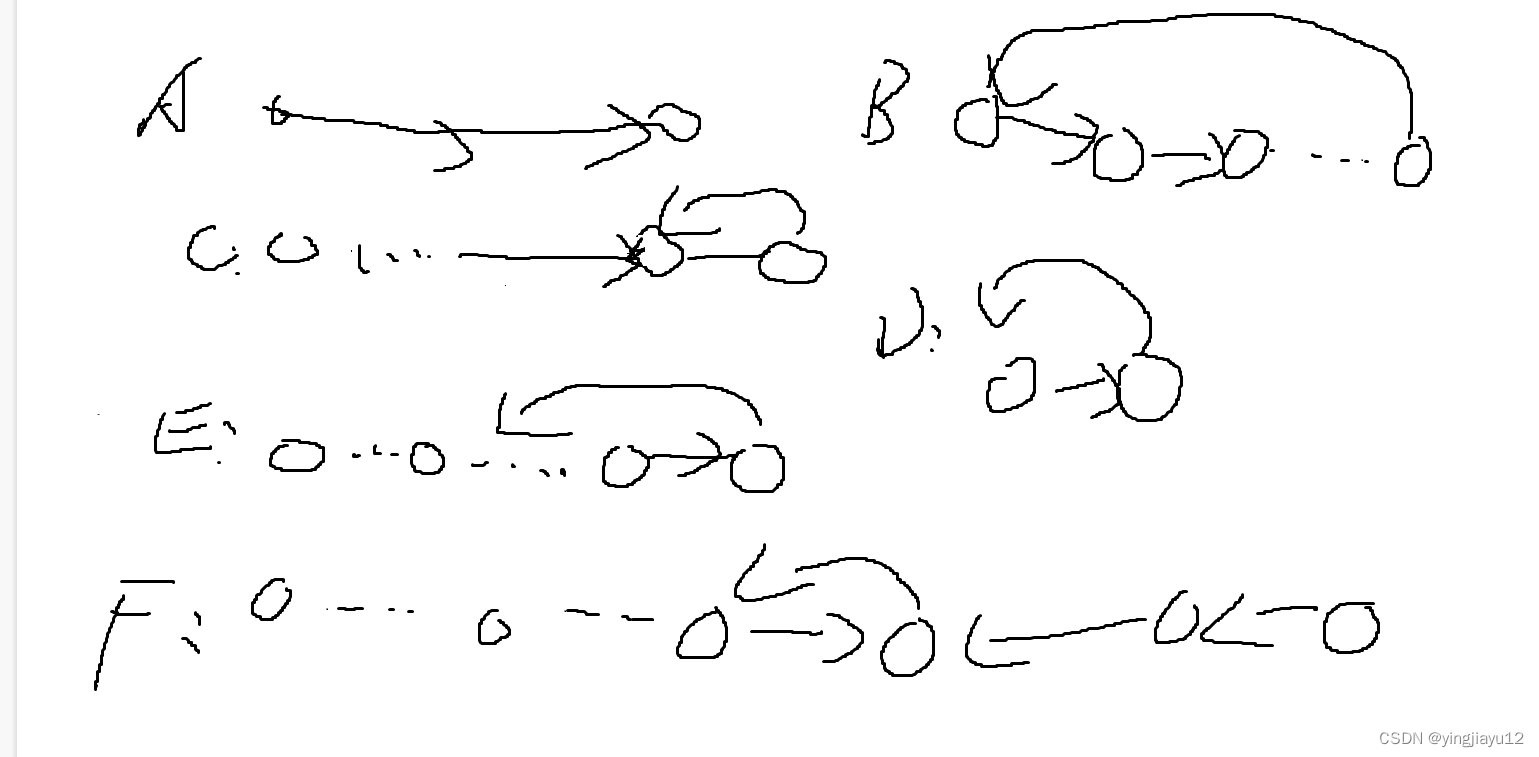
在这里插入图片描述

先简单解释一下为什么E情况是不存在的:因为假设这种情况存在的话,那么中间的那一个点将会有三个邻居,这样显然是不满足题意的.
先规定一下:我们将一个联通块在本题中称之为链,当且仅当该联通块能与其他同为链的联通块进行相连(也就是首尾两个位置的数并没有规定邻居).我们将一个联通块称之为环,当且仅当该联通块不能与其他联通块相连(也就是首尾两个位置的数已经被规定了邻居).
那么我们显然会发现,ACDF皆为链,只有B这种情况为环.当时我被hack了就是没有考虑F这种情况…
那么我们想得到最小答案,显然是将所有的链连成一块,然后加上环的个数.
我们想得到最大答案,显然就是环的个数+链的个数.
对于链的个数,显然我们可以使用拓扑排序来求,但是由于D的原因,我们又需要判断是否存在二元环,因为F的存在,我们有需要记录当前拓扑序属于第几个联通块.具体实现方式建议结合代码食用,使用文字不太能讲的明白

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];int vis[maxn];
vector<int>edge[maxn];int flag=1;int in[maxn];int cnt=0;
map<int,map<int,int> >mp;
void DFS(int u) {for(int i=0;i<edge[u].size();i++) {int v=edge[u][i];if(vis[v]) {if(vis[v]==cnt) {if(mp[u][v]==mp[v][u]) continue;//判断是否是因为二元环而重复,二元环将被当做链else {flag=0;return ;//如果不是那就是环了}}else {flag=-1;return ;//这里用来判断是否是F这种情况,也就是遍历到了一个之前遍历过的点,那么显然当前点应该是属于之前那个联通块的,此时不能重复累加}} if(flag!=1) return ;vis[v]=cnt;DFS(v);}
}
int main() {int T=read();while(T--) {int n=read();mp.clear();for(int i=1;i<=n;i++) {edge[i].clear();vis[i]=0;in[i]=0;}for(int i=1;i<=n;i++) {a[i]=read();in[a[i]]++;edge[i].push_back(a[i]);mp[i][a[i]]=1;}int cnt1=0,cnt2=0;for(int i=1;i<=n;i++) {if(in[i]==0) {flag=1;++cnt;vis[i]=cnt;DFS(i);if(flag==1) cnt1++;}}for(int i=1;i<=n;i++) {if(vis[i]==0) {++cnt;flag=1;vis[i]=cnt;DFS(i);if(flag==1) cnt1++;else cnt2++;}}cout<<cnt2+(cnt1?1:0)<<" "<<cnt1+cnt2<<endl;}return 0;
}

F题:F. Ira and Flamenco

发现我们需要选取 $m$ 个不同的数字,并且还要保证没两个数的差要小于 $m$ .那么很显然,我们找的这 $m$ 个数字应该是连续的.也就是 $k, k + 1, k + 2 . . . k + m - 1$ 这样陈列的.
发现位置不同算不同的情况,所以考虑对原数列进行离散化.统计每一个数字出现的次数,然后对于最终的选取方案乘上相应的倍数即可.并且我们也可以对原数列进行排序,这些操作显然都不会对最终的答案产生任何影响.
然后这道题就十分简单了.我们考虑使用双指针,每一次都找到一段合法的连续数字区间(此时可以不需要考虑区间的长度,当然考虑也没关系,但是由于我是用不考虑的方法做的,所以我接下来也是基于不考虑的方法来讲解的),对于当前区间,假设我们的长度刚好是 $m$ ,那么显然当前选取方案就是区间内所有数字的个数的乘积.假设我们的长度小于 $m$ ,那么显然我们这段区间不满足,直接枚举下一段区间.假设我们的长度大于 $m$ ,那么我们将从刚开始的 $[l, l + m - 1]$ 开始逐个记录每一个满足区间的值.当我们区间移动时,我们当前区间的贡献应该是上一个区间的贡献除移除的左端点的贡献乘上加入的右端点的贡献.因为需要取模,所以需要使用逆元.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
#define int long long
const int mod=1e9+7;
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int n,m;int in_fac[maxn];
int qpow(int a,int b) {int ans=1;while(b) {if(b&1) ans=(ans*a)%mod;b>>=1;a=(a*a)%mod;}return ans;
}
int a[maxn];map<int,int>mp;
vector<int>v;
signed main() {int T=read();while(T--) {n=read();m=read();mp.clear();v.clear();for(int i=1;i<=n;i++) {a[i]=read();v.push_back(a[i]);mp[a[i]]++;}if(m==1) {cout<<n<<endl;continue;}sort(v.begin(),v.end());v.erase(unique(v.begin(),v.end()),v.end());int l=0,r=0;int ans=0;while(r<v.size()) {if(r+1<v.size()&&v[r+1]-v[r]==1) r++;else {if(r-l+1>m) {int sum=1;for(int i=l;i<=l+m-1;i++) {sum=(sum*mp[v[i]])%mod;}ans=(ans+sum)%mod;while(l+m<=r) {l++;int R=l+m-1;sum=sum*mp[v[R]]%mod;sum=sum*qpow(mp[v[l-1]],mod-2)%mod;ans=(ans+sum)%mod;}l=r+1;r=l;}else if(r-l+1==m){int sum=1;while(l<=r) {sum=(sum*mp[v[l]])%mod;l++;}r=l;ans=(ans+sum)%mod;}else {l=r+1;r=l;}}}cout<<ans<<endl;}	return 0;
}

G题:G. Ksyusha and Chinchilla

本题是阳了的那天补的.做的时候迷迷糊糊.

其实本题的规律应该不是很难找.很容易发现对于一个节点 $u$ 来说,如果它同时有大小为一的儿子和大小为2的儿子,此时我们肯定是无法构造的.因为1,2都需要u来进行消除.又或者它同时有超过2个的大小为1的儿子或者超过一个的大小为2的儿子,也是无法构造的.

此时我们应该想到了一个基本的构造方案.所以我们考虑从下往上进行构造.在构造的过程中,我们一旦发现存在上述情况就直接退出,然后输出 $- 1$ .为了讨论方便起见,不妨另当前的这棵树是满足题意的.诶,写到这发现想要继续讨论下去,需要插播一条证明:下面来证明一下对于一个可满足题意的树来说,当每一个节点u的大小为3的倍数时,此时我们的u子树可以自行消除,不需要其他节点
可以使用反证法来证明,如果当前u子树需要其他节点.那么我们此时的总结点数就是3的倍数加上1或2(更大的显然没必要,因为最大只需要2).又因为对于一个可满足的树来说,我们每一次消除,减少的是3,所以总的节点数应该是3的倍数,这样就与这个事实矛盾了.又因为该子树是不是不可满足的,又是三的倍数,所以不需要其他节点.证毕.
此时我们考虑将所有子树的大小对3取模,对于模后结果为0的儿子v,我们直接加入<u,v>这条边即可.
对于模后结果为1的子树,我们将其当做一个大小为1的儿子(注意这里为什么能这么等价,因为我们递归到现在都是可满足的,所以这个子树中模后结果为3的任何一个更小的子树都是可删除的).对于模后结果为2的子树,我们将其当做一个大小为2的儿子即可.

还需要注意的一点细节是我们的根节点也是需要消除的,这个在dfs中是没办法保证的,但是我们可以通过n%3==0来保证

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define	int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
vector<int>edge[maxn];int Size[maxn];
map<int,map<int,int> >mp;
int flag=1;vector<int>Ans;
void dfs(int u,int per_u) {Size[u]=1;int cnt1=0,cnt2=0;for(int i=0;i<edge[u].size();i++) {int v=edge[u][i];if(v==per_u) continue;dfs(v,u);Size[u]+=Size[v];if(Size[v]%3==0) Ans.push_back(mp[u][v]);else if(Size[v]%3==1) cnt1++;else cnt2++;}if(cnt1&&cnt2) flag=false;if(cnt1>2) flag=false;if(cnt2>1) flag=false;
}
int main() {int T=read();while(T--) {int n=read();mp.clear();Ans.clear();flag=1;for(int i=1;i<=n;i++) {edge[i].clear();Size[i]=0;}for(int i=1;i<=n-1;i++) {int u=read(),v=read();mp[u][v]=mp[v][u]=i;edge[u].push_back(v);edge[v].push_back(u);}if(n==3) {cout<<0<<endl<<endl;continue;}if(n<=2) {cout<<"-1"<<endl;continue;}dfs(1,0);if(flag==true&&n%3==0){cout<<Ans.size()<<endl;for(int i=0;i<Ans.size();i++) {cout<<Ans[i]<<" ";}cout<<endl;} else {cout<<"-1"<<endl;}}return 0;
}

今日迷思:
有些事情对周围的人都不太好表达,自己选择一直憋着也挺难受的.反正这篇博客应该是不会被熟人看到的,就选择在这里倾诉一下了.
就在写这篇博客的今天,我决定和我的室友决裂了.这个室友可以说是我刚入大学时就准备一起打三年ACM的队友.我们一起在大一就拿了邀请赛的铜牌(虽然只是铜,但是在一个ACM弱校中感觉已经是难能可贵了).但是我们之间发生一些已经无法经过交涉能解决的事情了.就像"一起同过窗"中的一样.我甚至不如剧中的肖海洋,简直可以称作为一个joker.而且是在某人的见证下一步步成为joker的.更令人绝望的是假设我今日没有知道真正的事实,可能会一直成为joker下去.简直是无法在忍受了。但是我们之间又有着各种共同的交集.首先是室友,平时一起的事情就比较多,同时也有各种相同的朋友,相同的导师…这些都挺让我绝望的.最烦的是还有一个大创和ACM在,大创还已经申报上去了.继续大创是不可能了,我在那个大创队伍中呆一秒钟都简直想紫砂.刚刚经过磨练过的ACM队伍也要被拆散了(一个团队竞赛中两个队员存在敌对关系显然是不可能提升的).我感觉唯一的解决方案可能就是我退出大创队伍,然后让他退出我们的ACM队伍中了.虽然这样子我们队伍会元气大伤，那也总要比一直尴尬下去要好。

五月28号的湘潭邀请赛可能是我们的散伙赛了。希望能带他们拿一个银牌，就拿这个银牌来了断全部琐事吧。

加训加训!