Lin X, Tian W, Zhang W, et al. The leaderless multi-AUV system fault-tolerant consensus strategy under heterogeneous communication topology[J]. Ocean Engineering, 2021, 237: 109594.

1 Introduction

Autonomous underwater vehicle (AUV)
fault-tolerant consensus control (FTCC)
partial loss of effectiveness (PLOE)
active faulttolerant consensus control (AFTCC)

2 Preliminaries and problem formulation

2.1 Graph theory

$G_p$
$V_p$
${\epsilon }_{mn}$
$N_i(G(t))$
$Vs$
$L(G_s(t))$
$l{s}_{mn}$

2.2 The AUV dynamic model

6-DOF (degree of freedom)

Shipbuilding and Marine Engineering (SNAME)
the International Pool Conference (ITTC)

---

This article selects the torpedo-like AUV to study, whose rolling impact on translational motion so small that the speed of rolling has been neglected in the passage. This Kinematics model shows in equation (2), and the Kinetics model expresses in equation (3), respectively.
译文: 本文选取鱼雷型AUV作为研究对象，其横滚对平动运动的影响很小，因此在航道中忽略了横滚的速度。该运动学模型如式(2)所示，动力学模型如式(3)所示。

$$\dot{\eta }=J(\eta )v\text{\hspace{1em}(2)}$$

$$(M_A+M_R)\dot{v}+C_R(v)v+Y(v)v+g_M(\eta )=F{T}_{\tau }\text{\hspace{1em}(3)}$$

${\eta }_i=[x_i,y_i,z_i,{\theta }_i,{\psi }_i{]}^{\text{T}}\in {\mathbb{R}}^5$ 表示位置状态
$v_i=[u_i,v_i,w_i,q_i,r_i{]}^{\text{T}}\in {\mathbb{R}}^5$ 表示速度状态
$J(v)$ 雅各比 Jacobian 矩阵
$M_R$ 惯性矩阵 inertia matrix
$M_A$ 额外的惯性矩阵 additional inertia matrix
$C_R(v)$ 科里奥利矩阵 Coriolis matrix
$Y(v)$ 阻尼和向心矩阵 the damping and centripetal matrix.
$g_M(\eta )$ 是个向量，表示广义浮力和重力，这里等于 0
$F{T}_{\tau }$ 是 AUV 的控制器输入

---

AUV 的模型可以转换为
$$\left[\begin{array}{c}\dot{\eta }\\ \dot{v}\end{array}\right]=\left[\begin{array}{cc}I& 0\\ 0& -M_T^{-1}\end{array}\right]\left[\begin{array}{c}J(\eta )v\\ Q(\eta ,v)\end{array}\right]+\left[\begin{array}{c}0\\ M_T^{-1}\gamma (\varsigma )\end{array}\right]F{T}_{\tau }$$

然后将标准非线性函数模型简化为

$$\dot{\varsigma }=f(\varsigma )+g_M(\varsigma )\cdot F{T}_{\tau }\text{\hspace{1em}(5)}$$

$$h=\mu (\varsigma )\text{\hspace{1em}(6)}$$

$\varsigma =[{\eta }^{\text{T}},v^{\text{T}}{]}^{\text{T}}$
$\mu (\varsigma )=\eta$
$M_T=M_A+M_R$
$f(\varsigma )=\left[\begin{array}{cccc}{f}_1(\varsigma )& f_2(\varsigma )& \cdots & f_{10}(\varsigma )\end{array}\right]=\left[\begin{array}{cc}{I}_5& 0\\ 0& -M_T^{-1}\end{array}\right]\left[\begin{array}{c}J(\eta )v\\ Q(\eta ,v)\end{array}\right]$
$g(\varsigma )=\left[\begin{array}{cccc}{g}_1(\varsigma )& g_2(\varsigma )& \cdots & g_5(\varsigma )\end{array}\right]=\left[\begin{array}{c}0\\ M_T^{-1}\gamma (\varsigma )\end{array}\right]$
$\gamma (\varsigma )=[{\gamma }_{ij}(\varsigma )]\in {\mathbb{R}}^{5\times 5}$

---

$$u=B(\varsigma )+\Gamma (\varsigma )F{T}_{\tau }\text{\hspace{1em}(7)}$$

$B(\varsigma )={\left[\begin{array}{ccccc}{L}_f^2{h}_1(\varsigma )& L_f^2{h}_2(\varsigma )& L_f^2{h}_3(\varsigma )& L_f^2{h}_4(\varsigma )& L_f^2{h}_5(\varsigma )\end{array}\right]}^{\text{T}}$
$\Gamma (\varsigma )=[{\Gamma }_{ij}(\varsigma )]=\left[\begin{array}{c}{L}_{kj}{L}_f{h}_i(\varsigma )\end{array}\right]\in {\mathbb{R}}^{5\times 5}$

---

$$\begin{array}{r}{\dot{x}}_i=v_i\\ {\dot{v}}_i=u_i\end{array}\text{\hspace{1em}(8)}$$

---

2.3 Problem formulation

引入 $N$ 个 AUV，第 $k$ 个 AUV 的动态表示为（9）
$$\begin{array}{r}{\dot{s}}_k(t)=v_k(t)\\ {\dot{v}}_k(t)=u_k^o(t)\end{array}\text{\hspace{1em}(8)}$$

$u_k^o(t)$ 表示 AUV 执行器的输出

考虑执行器出故障时，用下式表示
$u_k^o(t_k)={\rho }_i(t_k)u_i(t_k)$

$u_i(t_k)$ 是名义上的
${\rho }_i(t_k)$ 是表示出现故障的对角矩阵，元素在(0,1)之间取值，$r_{ik}(t_k)=1$ 表示无故障

---

$Ls(G(t))$ 表示位置通信拉氏矩阵
$Lv(G(t))$ 表示速度通信拉氏矩阵

---

3 Main results

分布式 FTCC 协议为：
$$\begin{array}{rl}{u}_i(t)& ={{\chi }_i}^{-1}(t)u_i^h(t)\\ u_i^h(t)& =-k_1\sum _{j\in N_i}l{s}_{ij}\cdot s_j(t)-k_2\sum _{j\in N_i}l{v}_{ij}\cdot v_j(t)\end{array}$$

$k_1>0$

${\chi }_i(t)$：表示第 $i$ 个 AUV 执行器的估计值
$u_i^h(t)$：表示理想控制器
$u_i^o(t)$：执行器的实际输出
$u_i^e(t)$：执行器的实际输出与理想输出的差值

如果 ${\rho }_i(t)={\chi }_i(t)$，那么 $u_i^o(t)=u_i^h(t)$

---

同时误差可以有如下描述：
$$\begin{array}{rl}{u}_i^e(t_k)& =u_i^o(t_k)-u_i^h(t_k)\\ & =({\rho }_i(t_k)-{\chi }_i(t_k))\cdot {\chi }_i^{-1}(t_k)u_i^h(t_k)\\ & ={\tilde{\rho }}_i(t_k)u_i^h(t_k)\end{array}$$

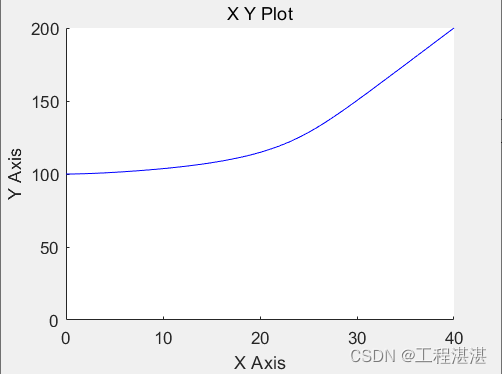
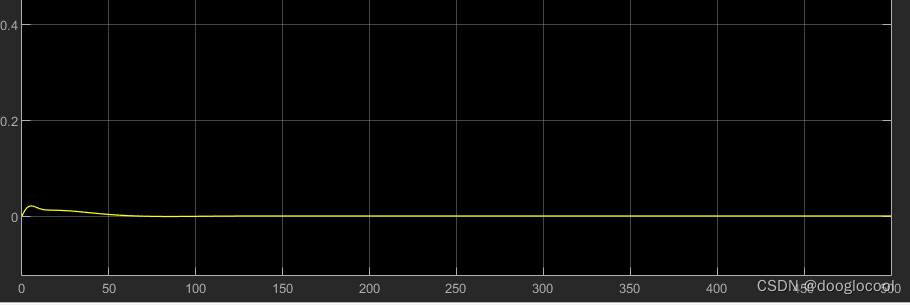
4 Numerical example

位置和速度通信拓扑图分别为 $G_1$ 和 $G_2$
$G_1=\left[\begin{array}{ccccc}1& 0& 0& 0& -\frac{1}{1}\\ -\frac{1}{1}& 1& 0& 0& 0\\ 0& -\frac{1}{1}& 1& 0& 0\\ 0& 0& -\frac{1}{1}& 1& 0\\ 0& 0& 0& -\frac{1}{1}& 1\end{array}\right]$

$G_2=\left[\begin{array}{ccccc}1& 0& 0& 0& -\frac{1}{1}\\ 0& 1& 0& -\frac{1}{1}& 0\\ -\frac{1}{1}& 0& 1& 0& 0\\ 0& 0& -\frac{1}{1}& 1& 0\\ 0& -\frac{1}{1}& 0& 0& 1\end{array}\right]$

---