1. 不同路径 I Unique Paths 1

2. 不同路径 II Unique Paths 2

3. 不同路径 III Unique Paths 3

🌟 每日一练刷题专栏 🌟

Golang每日一练专栏

Python每日一练专栏

C/C++每日一练专栏

Java每日一练专栏

1. 不同路径 I Unique Paths 1

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

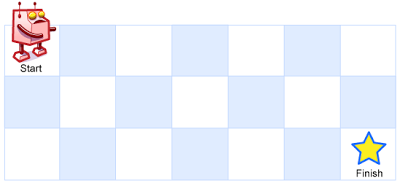
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9

之前练过，代码见：Python每日一练(20230410)_Hann Yang的博客

递归法：（不推荐，时间复杂度高）

class Solution:def uniquePaths(self, m: int, n: int) -> int:def backtrack(row, col):if row == 0 or col == 0:return 1return backtrack(row-1, col) + backtrack(row, col-1)return backtrack(m-1, n-1)

用组合公式，只要一行代码：

class Solution:def uniquePaths(self, m: int, n: int) -> int:return __import__('math').comb(m+n-2, m-1)# %%
s = Solution()
print(s.uniquePaths(m = 3, n = 7))
print(s.uniquePaths(m = 3, n = 2))
print(s.uniquePaths(m = 7, n = 3))
print(s.uniquePaths(m = 3, n = 3))

输出：

28
3
28
6

2. 不同路径 II Unique Paths 2

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

之前练过，代码见：Python每日一练(20230221)_Hann Yang的博客

递归法：（不推荐，时间复杂度高）

class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m, n = len(obstacleGrid), len(obstacleGrid[0])def backtrack(row, col):if row == m or col == n or obstacleGrid[row][col] == 1:return 0if row == m - 1 and col == n - 1:return 1return backtrack(row+1, col) + backtrack(row, col+1)return backtrack(0, 0)# %%
s = Solution()
print(s.uniquePathsWithObstacles(obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]))
print(s.uniquePathsWithObstacles(obstacleGrid = [[0,1],[0,0]]))

输出：

2
1

3. 不同路径 III Unique Paths 3

在二维网格 grid 上，有 4 种类型的方格：

1 表示起始方格。且只有一个起始方格。
2 表示结束方格，且只有一个结束方格。
0 表示我们可以走过的空方格。
-1 表示我们无法跨越的障碍。

返回在四个方向（上、下、左、右）上行走时，从起始方格到结束方格的不同路径的数目。

每一个无障碍方格都要通过一次，但是一条路径中不能重复通过同一个方格。

示例 1：

输入：[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出：2
解释：我们有以下两条路径：
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

示例 2：

输入：[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出：4
解释：我们有以下四条路径： 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

示例 3：

输入：[[0,1],[2,0]]
输出：0
解释：
没有一条路能完全穿过每一个空的方格一次。
请注意，起始和结束方格可以位于网格中的任意位置。

提示：

1 <= grid.length * grid[0].length <= 20

代码： 回溯法

from typing import List
class Solution:def uniquePathsIII(self, grid: List[List[int]]) -> int:m, n = len(grid), len(grid[0])start, end = None, Noneempty_count = 0# 找到起点、终点和空方格总数for i in range(m):for j in range(n):if grid[i][j] == 0:empty_count += 1elif grid[i][j] == 1:start = (i, j)elif grid[i][j] == 2:end = (i, j)# 记录已访问的坐标visited = set()def backtrack(row, col, count):# 矩阵边界检查if row < 0 or row >= m or col < 0 or col >= n:return 0# 障碍检查if grid[row][col] == -1:return 0# 到达终点检查if (row, col) == end:if count == empty_count + 1:return 1else:return 0# 已经经过或已经访问if (row, col) in visited:return 0# 标记为已经访问visited.add((row, col))# 向四个方向前进paths_count = 0paths_count += backtrack(row+1, col, count+1)paths_count += backtrack(row-1, col, count+1)paths_count += backtrack(row, col+1, count+1)paths_count += backtrack(row, col-1, count+1)# 回溯visited.remove((row, col))return paths_countreturn backtrack(start[0], start[1], 0)#%%
s = Solution()
grad = [[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
print(s.uniquePathsIII(grad))
grad = [[1,0,0,0],[0,0,0,0],[0,0,0,2]]
print(s.uniquePathsIII(grad))
grad = [[0,1],[2,0]]
print(s.uniquePathsIII(grad))

输出：

2
4
0