面试题

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中？

解决方法：

遍历，时间复杂度O(N)

使用set/uordered_set遍历40亿个数字，但是40亿个数字加载到内存中代价太大（需要占用4个G左右的内存大小），不现实

排序(O(NlogN))，利用二分查找(O(logN))

排序无法加载到内存中进行排序（代价太大，需要一次性开4G大小的空间），那就必须使用外排序在磁盘上排序，但是外排序的效率很低，不符合快速的特点，不能很好支持快速随机访问

位图

数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，那么可以使用一个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0代表不存在，如下图：

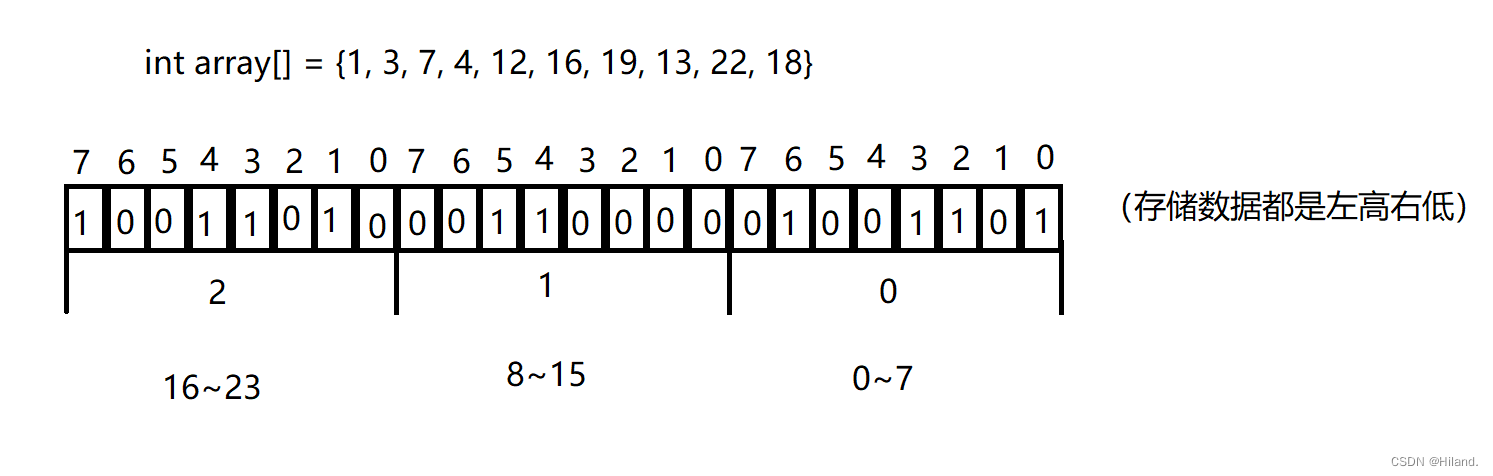
位图概念

所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的。

位图的实现

#pragma once 
#include <vector>/** 位图本质上是由于需要处理海量的数据，将数据映射到比特位上来处理，大大缩小了空间的消耗*/namespace mystl
{//使用非类型模板参数接收数据量template<size_t N>class bitset{public:bitset(){_bit.resize(N/8+1, 0);//确保每一个位置都有对应的比特位需要+1}//将需要查找的数据映射到位置，即将对应位置设为1void set(size_t x){size_t i = x / 8;//确定在第几个字节的位置size_t j = x % 8;//确定在第i个字节中的第几个比特位_bit[i] |= (1 << j);}//将数据删除，即将对应的位置设为0void reset(size_t x){size_t i = x / 8;size_t j = x % 8;_bit[i] &= (~(1<<j));//将对应位置设为0，其他位置设为1，按位与后就能够不影响其他位置}//查找一个数据是否存在bool test(size_t x){size_t i = x / 8;size_t j = x % 8;return _bit[i] & (1<<j);}private:std::vector<char> _bit;//可以使用char/int来分割比特位};
}

主要难度在于将得到的数据转化成对应在比特位的位置上，根据vector中存储的数据来算数据对应在比特位上的位置

位图的应用

应用一

给定100亿个整数，没排过序，设计算法找到只出现一次的整数？

上个问题就像是K模型，而这个问题就像是KV模型，分析题目知道数据的最大值为INT_MAX，而题目也只是要找只出现一次的整数，那我们统计状态只需要统计出现0次，1次，以及>=2次三种状态，而统计三种状态只需要两个比特位即可，由此可以使用两个bitset来实现封装two_bitset，分别表示00，01，10三种状态即可，一个bitset对象存储第一个比特位状态，一个bitset对象存储第二个比特位状态，实现如下：

#pragma once
template<size_t N>class two_bitset{public://set封装bitset来表示00，01，10void set(size_t x){int n1 = _bit1.test(x);int n2 = _bit2.test(x);//00是为出现，01是出现一次，10是出现>=2次if(n1 == 0 && n2 == 0)_bit2.set(x);else if(n1 == 0 && n2 == 1){_bit1.set(x);_bit2.reset(x);}}//01才是只出现一次bool is_once(size_t x){return !_bit1.test(x) && _bit2.test(x);}private:bitset<N> _bit1;//表示第一个比特位bitset<N> _bit2;//表示第二个比特位};

应用二

给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

本质上是使用两个位图来存储每个数据的状态，位图一存储文件一中100亿个整数的状态，位图二存储文件二中100亿个整数的状态，两个文件中的数据最大值是INT_MAX，一个文件中状态的存储需要消耗512MB左右，两个文件正好占用1G内存左右，对比两个位图每一位的状态，即可得到两个文件的交集，代码如下：

#include <iostream>
#include <bitset>
using namespace std;int main()
{bitset<-1> bs1;bitset<-1> bs2;//举例读取十个数据for(int i = 0; i < 10; ++i){int input1 = 0;int input2 = 0;bs1.set(input1);bs2.set(input2);}//找到交集并输出for(int i = 0; i <= INT_MAX; ++i)if(bs1.test(i) && bs2.test(i))cout << i << endl;return 0;
}

位图应用变形

1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

和找只出现一次的所有整数思路一致，00表示没有出现过，01表示出现过一次，10表示出现过两次，11表示出现过的次数>=3次，正好两个比特位只能表示最多四种状态，只需要统计00，01，10的情况即可，实现如下：

#pragma once
template<size_t N>class two_bitset{public://set封装bitset来表示00，01，10，11void set(size_t x){int n1 = _bit1.test(x);int n2 = _bit2.test(x);//00是为出现，01是出现一次，10是出现>=2次if(n1 == 0 && n2 == 0)_bit2.set(x);else if(n1 == 0 && n2 == 1){_bit1.set(x);_bit2.reset(x);}else if(n1 == 1 && n2 == 0)_bit2.set(x);}//统计00，01，10即不超过两次bool Not_more_than_twice(size_t x){//除了11以外都是不超过两次，因为两个比特位只能表示四种状态if(_bit1.test(x) == 1 && _bit2.test(x) == 1)return false;return ture;}private:bitset<N> _bit1;//表示第一个比特位bitset<N> _bit2;//表示第二个比特位};