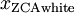先看下wiki上关于whiten transformation的介绍,简言之就是:把具有协方差的变量转换为协方差为单位矩阵的变量,即转换后,变量间不相关,且方差为1。之所以称之为'whiten',是由于该处理将输入向量转换为白噪声向量。第二行是介绍3种和白化功能类似的处理:去相关变换、归一化变换和色彩变换。
A whitening transformation or sphering transformation is a linear transformation that transforms a vector of random variables with a known covariance matrix into a set of new variables whose covariance is the identity matrix, meaning that they are uncorrelated and each have variance 1.[1] The transformation is called "whitening" because it changes the input vector into a white noise vector.Several other transformations are closely related to whitening: 1) the decorrelation transform removes only the correlations but leaves variances intact, 2) the standardization transform sets variances to 1 but leaves correlations intact, and 3) a coloring transformation transforms a vector of white random variables into a random vector with a specified covariance matrix.[2]信号处理中,白噪声是指在功率谱上,不同频率具有相同功率值的随机信号。常见的高斯白噪声是指功率谱密度服从均匀分布,幅值分布服从高斯分布。
 |  | |
| 图片来自这里 | 高斯白噪声的功率谱 | 高斯白噪声的幅值分布 |
概念性的东西介绍完了,接下来看下如何实现whiten。
可详细查看UFLDL中白化的例子即对应代码。
顺带和大家分享篇关于《奇异值分解》的博客。
参考文献:
- http://courses.media.mit.edu/2010fall/mas622j/whiten.pdf
- http://deeplearning.stanford.edu/wiki/index.php/%E7%99%BD%E5%8C%96
- http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html