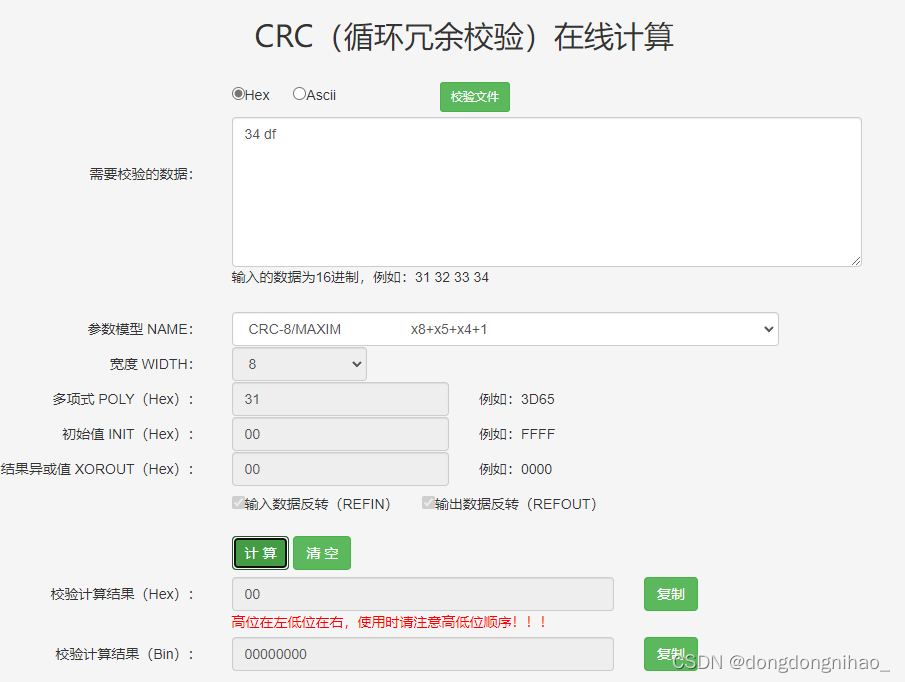
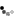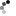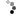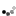香农在其著名的论文《A mathematical theory of communication》中提出了信道编码定理,在传输速率小于信道容量的情况下,可以通过编码非常高效的提高传输的可靠性。我们现在所说的信道编码主要指的是纠错编码,比如卷积码,汉明码,Turbo码和LPDC码等等。本文主要研究在这些编码技术中比较常用的一种检验技术,即CRC。
CRC技术也是通过增加信道的冗余来提高传输的可靠性,不但能够起到校验的作用同时也具备一定的纠错能力。CRC算法的实现是基于循环码的,其数学原理在于通过发射端信息做一个多项式除法,得到余数作为检验位,然后将其加入原始信息的后面。在接收端提取发射端的数据位然后做相同的求余运算,再将计算出的校验位和发送数据带有的检验位相对比,若相同则说明数据是正确的,若不同说明数据是错误的。下图展示了一个简单的CRC结构:

前面说了CRC的原理是做除法取余数,这里就涉及了一个除法项,我们称之为生成多项式(Generator Polynomial),这个生成多项式是发送机和接收机两端约定好的一个二进制序列,在整个传输过程中保持不变。这个生成多项式同时满足如下几个条件:
- 最高位和最低为为1
- 当传输信息任何1位发生错误时,被其除后余数不为0
- 不同位数发生错误时,余数不同。
- 对于余数做除法,应使余数循环。
这里我们以一个简单的CRC-4为例,来解释生成多项式的作用和CRC校验的原理:
CRC-4的常用的一个生成多项式为:
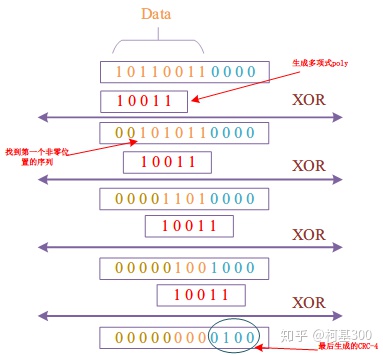
最后的发送数据就为:
其实现的Matlab代码如下:
InputBits 最终输出的结果为:

和上面手算的相同。
软件仿真结束后我们就可以开始使用硬件进行实现了,我个人实现的思路是通过状态机来实现上述matlab代码中的循环运算,首先设定一个数据位宽长度计数器width cont,每当进来一次有效的数据,判断其最高位是否为1,若否则左移一位,width cont减1,找到其最高位为1的数据后进入下一个状态进行xor运算,在xor状态中将数据和poly 序列进行xor运算,随后在进入刚才的判断状态,找到最高位为1的位置,直到width cont < poly序列的长度时结束计算,然后保存余数,跳入等待下一个有效数据计算的状态。正当我兴致冲冲打算去码代码的时候,发现了一个神奇的网站可以直接生成CRC校验的代码。。。
CRC Generation Toolwww.easics.com
只要选择好poly多项式和数据位宽就可以直接生成verilog代码,十分方便:
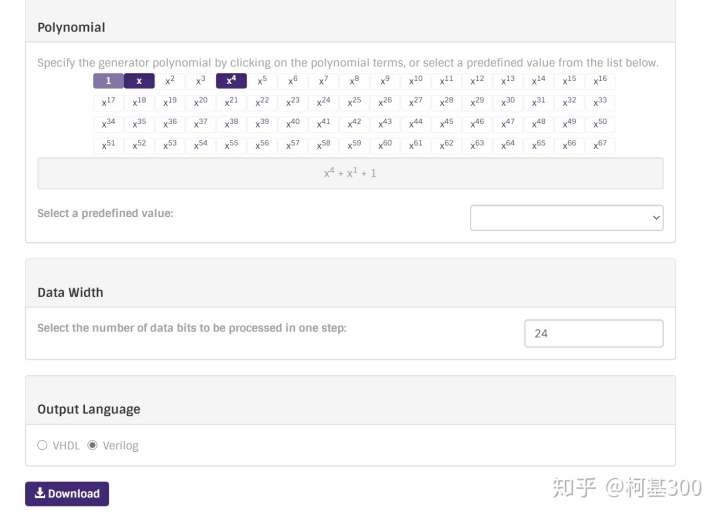
生成代码如下:
// polynomial: x^4 + x^1 + 1
这是个函数形式的代码,并且通过并行的形式直接可以计算出CRC的几个余数,效率简洁高效,我暂时还没看懂这个代码是什么原理,懂得大佬可以指点一下。
随后在发射端只要进行一个简单的CRC编码:
always 接收端校验使用的方法为:
always 具体的仿真结果这里就没有做了,等有空再补上~
参考文献
[1] 王栋. 基于CRC的多比特纠错算法研究与实现[D].西安电子科技大学,2013.