解读CRC校验计算

个人随笔 (Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu)

参考：http://www.sunshine2k.de/articles/coding/crc/understanding_crc.html
参考：https://en.wikipedia.org/wiki/Cyclic_redundancy_check
参考：https://www.cnblogs.com/yikoulinux/p/14952297.html
参考：https://crccalc.com/

CRC校验定义：

循环冗余校验码（CRC – Cyclic Redundancy Checksum），简称循环码，是一种常用的、具有检错、纠错能力的校验码，在早期的通信中运用广泛。
循环冗余校验码常用于外存储器和计算机同步通信的数据校验。
A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to digital data.
最简单的错误检验方法，奇偶检验，实际上是一个1bit的CRC，它使用生成多项式x+1(0b11)，被成为CRC-1。
The simplest error-detection system, the parity bit, is in fact a 1-bit CRC: it uses the generator polynomial x + 1 (two terms),[3] and has the name CRC-1.

关于CRC校验的理解：

CRC校验的思路是，把一个串作为一个长的数值，附加某段校验码后，形成一个更长的数值串，对该数值串求余运算时能够整除；从而来校验内容未被篡改；
求余运算和每一位的数值都相关，所以校验码会受其每一位修改的影响；
另外，能被整除的概率，和补取的校验码段长度相关，且通常只有一个取值是能整除的，对于1字节校验码来说，概率是1/256，对于4字节校验码来说，概率是1/2^32，校验正确率还是比较高的；
被附加的某段校验码就称之为CRC校验码。

按照这个校验思路，举个10进制的例子：
例如1位校验码，对9求余，1000这个数值校验时，先补全一位0，10000%9，得到值1111，余数1；
如果要整除，就要9-1，补一个8在后面；10008 % 9 可以整除。所以1000后面的CRC校验码就为8。

实际求余的计算，为了提升校验效率，采用的模二除法：
对于模二除法，与算术除法不同的是每一位除的结果不影响其他位，即不向上借位，所以实际上相当于二进制中的逻辑异或运算。
0 mod 1 = 1 --> 0 ^ 1 = 1
1 mod 0 = 1 --> 1 ^ 0 = 1
0 mod 0 = 0 --> 0 ^ 0 = 0
1 mod 1 = 0 --> 1 ^ 1 = 0
另外，模二加法，模二减法与这个规律也一致，也与异或效果一致
0 + 1 = 0 - 1 = 1
1 + 0 = 1 - 0 =1
0 + 0 = 0 - 0 = 0
1 + 1 = 1 - 1 = 0
模二乘法不同，和按位与& 结果一致 1 * 1 = 1 --> 1 & 1 = 1

对于异或算法来说：满足交换律，三者还能互为求值，非常适合互为计算（ps. 简单加密解密值非常适合)
a ^ b = b ^ a = c
a ^ c = c ^ a = b
b ^ c = c ^ b = a

这样来说，一个串str如果要获得它的CRC校验串，流程就是：
a. 对该串str补二进制0，补0的长度为crc校验码的二进制长度
b. 对补0后的串进行模二除法，获取到余数，余数就是补值 ( 0 ^ a = b --> b ^ a = 0)
c. 把补值放到该串str的后面，作为CRC校验码

对于所使用的除数，多项式规律为：
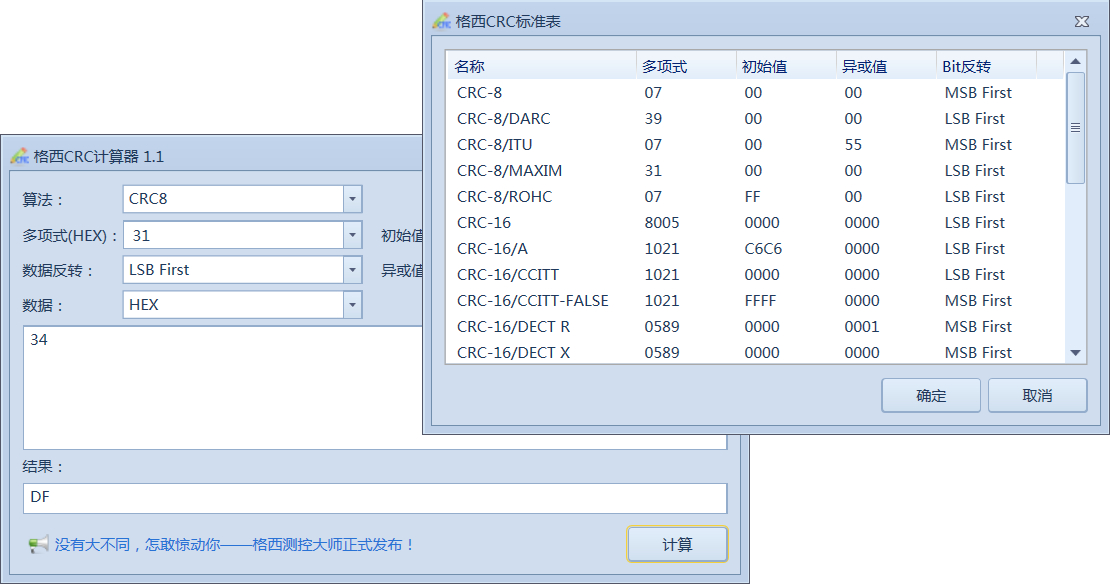
crc8 常用 x^8 + x^2 + x + 1，首位是比较对齐用，剩余值为 0x07，二进制逆序为 0xE0
crc16 常用 x^16 + x^15 + x^2 + 1，首位是比较对齐用，剩余值为 0x8005，二进制逆序为0xA001
crc32 常用 x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1，首位用于比较对齐，剩余值为 0x04C11DB7，二进制逆序为0xEDB88320

对于CRC的计算简化：

CRC计算时，一般都是使用查表法计算的；
假设一个字符串长度是一个字节，当明确多项式除数之后，那么它的CRC校验值，只可能有256中相对应，也即可以查表得到。
那么对于一个实际字符串来说，可以看作由一个1字节串，1字节串连接组成的长串；
计算时：
a. 把第一个字节的crc值获取到之后，带入到下一个字节的计算中；
b. 把crc首个字节与当前字节合并，合成值查表，获取到一个新的crc值，再把上一个crc的剩余字节移位后合并到crc新值上，得到合并后的值；
c. 依次类推，等到字符串末尾时，就获取到了最终的crc值；

CRC参数：

CRC的关键必选的参数是width和polynomial；CRC校验宽度width，例如8字节，16字节，32字节，标识了产生CRC校验值的位宽；CRC多项式polynomial，例如crc8常用的 x^8+x2+x+1，是crc校验所使用的除数。
除了关键必选参数外，crc扩展出了initVal初始值，xorValue结果xor值，refect-in输入值位镜像, refect-out输出值位镜像参数，增加了crc校验计算的复杂度；
综上这些参数的设定，也被分别应用到不同的领域，不同的场景。

8字节的一个例子：

对于8字节的计算，参考如下

unsigned char charcrc8(const unsigned char ch, bool reflect=false){unsigned char crc = ch;if (!reflect){const unsigned char polynomial = 0x07;for (int i=0; i<8; i++){if ((crc & 0x80) != 0)crc = (crc << 1) ^ polynomial;elsecrc <<= 1;}}else{const unsigned char polynomial = 0xE0;for (int i=0; i<8; i++){if ((crc & 0x1) != 0)crc = (crc >> 1) ^ polynomial;elsecrc >>= 1;}}return crc;
}
unsigned char calccrc8(const char* str, int count, unsigned char init = 0, bool reflect=false, unsigned char xorcrc = 0){unsigned char crc = init;for (int i=0; i<count; i++){crc = charcrc8(str[i] ^ crc, reflect);  }return crc ^ xorcrc;
}

简单的调用例子：

int main(int argc, char** argv)
{const char* str="123";if (argc >= 2) str = argv[1];for (int i=0; i<256; i++){printf("(%d->0x%02x-0x%02x) ", i, charcrc8(i), charcrc8(i, true));}printf("\n\n");printf("<%s> crc8 is 0x%02x, with reflect 0x%02x\n", str, calccrc8(str, strlen(str)), calccrc8(str, strlen(str), 0, true));return 0;
}

再附一些参考地址：

crc在线计算：https://crccalc.com/
crc计算方法：http://www.sunshine2k.de/articles/coding/crc/understanding_crc.html
reflect-table如何构建出来：https://stackoverflow.com/questions/28656471/how-to-configure-calculation-of-crc-table
crc在线计算：http://www.sunshine2k.de/coding/javascript/crc/crc_js.html

个人随笔 (Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu)