标题：VDO-SLAM: A Visual Dynamic Object-aware SLAM System

作者：Jun Zhang , Mina Henein , Robert Mahony and Viorela Ila

来源：https://arxiv.org/pdf/2005.11052.pdf

1.摘要

（1）一个具有鲁棒性的动态物体感知SLAM系统，利用语义信息在不带任何物体形状或运动模型等先验信息实现对场景中刚性物体的运动估计；

（2）提出将环境中将动态和静态结构集成到一个统一的估计框架，从而实现了精确的机器人姿态和空间地图估计。

2.引言

当前的SLAM系统不能在高动态环境下运行
SLAM中解决动态物体的传统手段

（1）将与移动物体有关联的的传感器数据看作外点并且移除他们；

（2）检测运动目标并且单独的使用传统的多目标追踪来跟踪他们（精确度依靠相机的位姿估计）。

VDO-SLAM是一个基于双目或RGB-D相机的语义信息动态SLAM系统

2.1 贡献：

（1）集成的统一估计框架；

（2）对动态物体SE（3）位姿变化精准的估计，计算场景中物体移动速度；

（3）鲁棒性更强的方法，能够处理语义对象分割失败导致的间接遮挡等问题；

（4）在复杂真实的场景中演示。

2.2 实现：

（1）运动分割；

（2）动态目标跟踪；

（3）估计相机姿态以及静态和动态结构；

（4）场景中每个刚性物体的完整SE（3）姿态变化；

（5）提取移动目标速度信息；

（6）在真实的户外场景中可以运行。

2.3 相关工作

（1）Hahnel 2003 ：Expectation-Maximisation（EM）期望最大化，更新对应于动态/静态对象的概率估计，并且删除对应动态估计的对象；

（2）Biddy and Reid 2007 ：利用广义EM算法估计3D特征（静态或动态）的状态，他们使用可逆数据关联将动态对象包含在一个单一的SLAM框架中；

（3）Wang 2007 ：提出移动目标追踪理论（SLAMMOT），SLAMMOT具有检测和跟踪移动物体，将估计问题分解成两个独立的估计问题（动态和静态物体）使实时更新过滤器成为可能；

（4）Kundu 2011 ：通过解决动态物体结构和并行追踪移动物体来解决动态物体SLAM问题，并且输出场景中包含静态和动态物体的结构和轨迹到一个三维动态地图；

（5）Alcantarilla 2012 ：使用稠密场景流对动态物体进行检测，并且通过从估计删除动态对象的“错误”测量结果而改进定位和建图的结果；

（6）Tan 2013 ：提出一种在线关键帧更新，可以可靠的检测特征（外观和结构）的变化，并在必要的时候丢弃他们；

（7）Zou and Tan 2013 ：提出一种多摄像机SLAM系统，它可以跟踪多个相机，同时重建静态背景点和移动前景点的三维位置；

（8）Reddy 2015 ：使用光学信息流和深度来计算语义运动分割，在使用语义约束之前，单独的对静态和动态物体重建；

（9）Judd 2018 ：通过多运动视觉里程计（MVO）多模型融合技术实现场景中相机和刚体的完整SE（3）运动；

（10）Yang and Scherer 2019 ：提出一种用于单一图像三维长方体检测方法，以及用于静态和动态环境的多视图对象SLAM。

Current state-of-the-art motion segmentation algorithms seek to combine methods。

（1）Elhamifar and Vidal 2009；Lai 2016 ：将放射假设和极几何集成到一个单一的框架中，以充分利用其优势；

（2）Xu 2018 ：引入了多帧光谱聚类框架，并结合了仿射模型、单应性模型和基本矩阵，利用语义信息被证明有助于处理退化运动和部分遮挡问题，提高运动分割精度。

在过去的几年中，多目标跟踪算法已经从传统的基于推理/滤波的方法发展到数据驱动（深度学习）的方法

3 方法

在本节中，我们将展示如何基于点跟踪以无模型方式对刚性对象的运动进行建模。我们建议使用因子图优化估计相机和物体运动。

在我们的系统的跟踪模块中，如图所示，系统优化的代价函数目的是估计相机姿势和移动对象的运动，代价函数与3D-2D重投影误差相关，并且定义在图像平面上。由于噪声在图像平面中的特征更好，这为相机定位提供了更准确的结果。此外，基于这个误差项，我们提出了一个新的公式，以联合优化光流与相机姿态和物体运动，以确保关键点跟踪的鲁棒性。在建图模块中，3D的误差代价函数用于优化3D结构和物体运动估计的最佳结果。转载自【https://blog.csdn.net/u013019296/article/details/108526116】

3.1 背景与标注

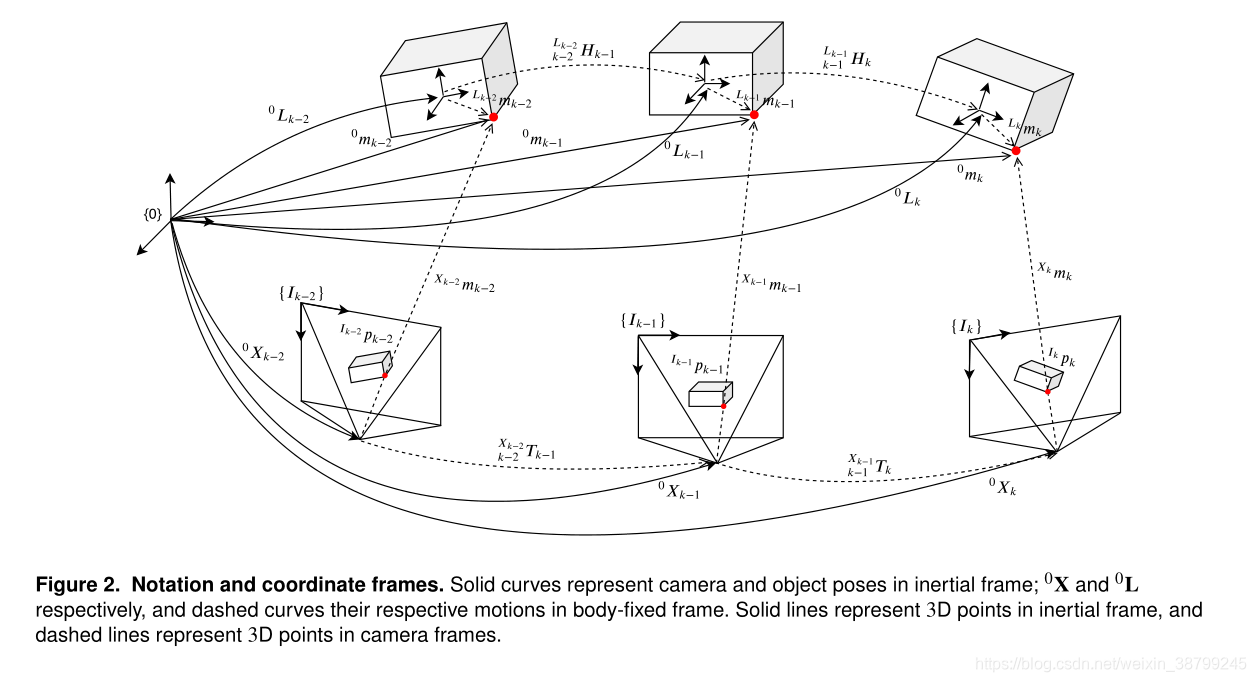
3.1.1 坐标系：

使 $_{}^{0}\textrm{X}_{k}$ ， $_{}^{0}\textrm{L}_{k}$ $\in$ $SE\left ( 3 \right )$ 分别为机器人/相机和物体在全局参考坐标系0（？可能为起始帧或世界坐标系）处时间为 $k$ 的3D姿态， $k\in J$ 设置为时间的步长。

3.1.2 点：

$_{}^{0}\textrm{m}_{k}^{i}$ ：在 $k$ 时第 $i$ 个3D点的齐次坐标， $_{}^{0}\textrm{m}_{}^{i}=[\textrm{m}_{x}^{i},\textrm{m}_{y}^{i},\textrm{m}_{z}^{i},1] \in \mathbb{E}_{}^{3}$ ， $i \in \mathbb{M}$ ，我们在机器人/相机坐标系下该点为（即将3D点转换为机器人/相机坐标系下坐标）： $_{}^{\textrm{X}_{k}}\textrm{m}_{k}^{i}=_{}^{0}\textrm{X}_{k}^{-1}\textrm{m}_{k}^{i}$ 。

$\textrm{I}_{k}$ ：参考帧，由相机在 $k$ (选择图像左上角)时捕获的图像。

$_{}^{\textrm{I}_{k}}\textrm{p}_{k}^{i}=[\textrm{u}_{}^{i},\textrm{v}_{}^{i},1] \in \mathbb{E}$ ：是参考帧 $\textrm{I}_{k}$ 对应齐次3D点 $_{}^{\textrm{X}_{k}}\textrm{m}_{k}^{i}$ 上的像素坐标：

通过投影函数 $\pi (\cdot )$ 获得： $_{}^{\textrm{I}_{k}}\textrm{p}_{k}^{i}=\pi (_{}^{\textrm{X}_{k}}\textrm{m}_{k}^{i})=\textrm{K}_{}^{\textrm{X}_{k}}\textrm{m}_{k}^{i}$ ，（1）

$\textrm{K}$ 为相机的内参。

$_{}^{I_{k}}\phi _{}^{i} \in \mathbb{R}_{}^{2}$ ：相机或物体运动都会产生光流，表示像素 $_{}^{\textrm{I}_{k-1}}\textrm{p}_{k-1}^{i}$ 从第 $I_{k-1}$ 帧运动到第 $I_{k}$ 帧位移矢量：

$_{}^{I_{k}}\phi _{}^{i} =_{}^{I_{k}}\widetilde{p}_{k}^{i}-_{}^{I_{k-1}}\textrm{p}_{k-1}^{i}$ ，（2）

$_{}^{I_{k}}\widetilde{p}_{k}^{i}$ 是 $_{}^{I_{k-1}}\textrm{p}_{k-1}^{i}$ 在 $I_{k}$ 中的对应。

我们利用光流来寻找连续帧之间的对应

3.1.3 目标和3D点移动：

物体在 $k-1$ 到 $k$ 时刻的运动由齐次转换 $_{k-1}^{L_{k-1}}\textrm{H}_{k}\in SE(3)$ 来描述：

$_{k-1}^{L_{k-1}}\textrm{H}_{k}=_{}^{0}\textrm{L}_{k-1}^{-1}\ {_{}^{0}\textrm{L}_{k}}$ ，（3）

图2以虚线形式表达了运动转换

在对应的物体坐标系中，我们把一个点写成： $_{}^{L_{k}}\textrm{m}_{k}^{i} = _{}^{0}\textrm{L}_{k}^{-1}\ {_{}^{0}\textrm{m}_{k}^{i}}$ ，如图二中从对象参考坐标系到红点的虚线表示。

将（3）中 $k$ 时刻的物体姿态替换为： $_{}^{0}\textrm{m}_{k}^{i}={}^{0}\textrm{L}_{k} \ _{}^{L_{k}}\textrm{m}_{k}^{i}=_{}^{0}\textrm{L}_{k-1} \ {_{k-1}^{L_{k-1}}\textrm{H}_{k}} \ _{}^{L_{k}}\textrm{m}_{k}^{i}$ ，（4）

对于刚性物体， $_{}^{L_{k}}\textrm{m}_{k}^{i}$ 在 $_{}^{L}\textrm{m}_{}^{i}$ 保持不变，所以有： $_{}^{L}\textrm{m}_{}^{i} = _{}^{0}\textrm{L}_{k}^{-1}\ {_{}^{0}\textrm{m}_{k}^{i}}= _{}^{0}\textrm{L}_{k+n}^{-1}\ {_{}^{0}\textrm{m}_{k+n}^{i}}$ ， $n\in\mathbb{Z}$ 。

对于刚性物体，当 $n=-1$ 时，公式（4）变成： $_{}^{0}\textrm{m}_{k}^{i}=_{}^{0}\textrm{L}_{k-1} \ {_{k-1}^{L_{k-1}}\textrm{H}_{k}} \ _{}^{0}\textrm{L}_{k-1}^{-1} \ _{}^{0}\textrm{m}_{k-1}^{i}$ ，（5）

(5)是至关重要的，因为它在连续的时间步上通过齐次变换 $_{k-1}^{\ \ \0}\textrm{H}_{k}:=_{}^{0}\textrm{L}_{k-1} \ _{k-1}^{L_{k-1}}\textrm{H}_{k} \ _{}^{0}\textrm{L}_{k-1}^{-1}$ 联系在一个运动的刚性物体上的相同的三维点，这个方程表示一个姿态变换的坐标系变化。

所以点在全局参考帧中表达为： $_{}^{0}\textrm{m}_{k}^{i}=_{k-1}^{\ \ \0}\textrm{H}_{k} \ _{}^{0}\textrm{m}_{k-1}^{i}$ ，（6）

公式(6)是我们的运动估计方法的核心，因为它以无模型的方式通过属于物体上的点表示刚性物体的姿态变化，而不需要将物体的三维姿态作为一个随机变量包括在估计中。

3.2 相机位姿和物体运动估计

3.2.1 相机位姿估计：

给一组静态3D点 $\left \{ _{}^{0}\textrm{m}_{k-1}^{i}\ | \ i \in \mathbb{M} \ , \ k \in \mathbb{J}\right \}$ 在全局参考坐标系下 $k-1$ 时刻被观测到，在图像 $\textrm{I}_{k}$ 上对应的2D点为 $\left \{ _{}^{I_{k}}\widehat{p}_{k}^{i} \ | \ i \in \mathbb{M} \ , \ k \in \mathbb{J}\right \}$ ，通过最小化投影误差估计相机姿态：

$\textrm{e}_{i}\left ( _{}^{0}\textrm{X}_{k} \right )=_{}^{I_{k}}\widehat{p}_{k}^{i}-\pi \left ( _{}^{0}\textrm{X}_{k}^{-1} \ _{}^{0}\textrm{m}_{k-1}^{i} \right )$ ，（7）

我们用李代数的元素 $\textrm{x}_{k} \in se\left ( 3 \right )$ 参数化SE(3)相机姿态：

$_{}^{0}\textrm{X}_{k}=exp\left ( _{}^{0}\textrm{x}_{k} \right )$ ，（8）

用vee运算符定义 $_{}^{0}\textrm{x}_{k}^{\nu }$ 为 $se\left ( 3 \right )$ 到 $\mathbb{R}_{}^{6}$ 的映射。

使用 $SE\left ( 3 \right )$ 的李代数，将（8）带入到（7），最小二乘法的解有下式给出：

$_{}^{0}\textrm{x}_{k}^{*\nu }=\mathop {argmin}_{_{}^{0}\textrm{x}_{k}^{\nu}}\sum_{i}^{n_{b}}\rho _{h}\left ( \textrm{e}_{i}^{\top }\left ( _{}^{0}\textrm{x}_{k} \right ) \sum_{p}^{-1}\textrm{e}_{i}\left ( _{}^{0}\textrm{x}_{k} \right )\right )$ ，（9）

在连续帧中， $n_{b}$ 为在3D-2D可见的静态背景对应点。

$\rho _{h}$ 时Huber函数，Σp是与重投影误差相关的协方差矩阵。

相机位姿由 $_{}^{0}\textrm{X}_{k}^{*}=exp\left ( _{}^{0}\textrm{x}_{k}^{*} \right )$ 给出，由列文伯格-马夸尔特法给出。

3.2.2 物体运动估计：

与相机位姿估计类似，构造了一个基于重投影误差的代价函数来求解目标运动 $_{k-1}^{\ \ 0}\textrm{H}_{k}$ 。

通过公式（6），在图像 $\textrm{I}_{k}$ 3D点到2D点映射的重投影误差为： $\textrm{e}_{i}\left ( _{k-1}^{\ \ 0}\textrm{H}_{k} \right ):=_{}^{I_{k}}\widetilde{p}_{k}^{i}-\pi \left ( _{}^{0}\textrm{X}_{k}^{-1} \ _{k-1}^{\ \ 0}\textrm{H}_{k} \ _{}^{0}\textrm{m}_{k-1}^{i} \right ) = _{}^{I_{k}}\widetilde{p}_{k}^{i}-\pi \left ( _{k-1}^{\ \ 0}\textrm{G}_{k} \ _{}^{0}\textrm{m}_{k-1}^{i} \right )$ ，（10）

其中 $_{k-1}^{\ \ 0}\textrm{G}_{k} \in SE\left ( 3 \right ):=exp\left ( _{k-1}^{\ \0}\textrm{g}_{k} \right )$ ， $_{k-1}^{\ \0}\textrm{g}_{k} \in se\left ( 3\right )$ ，

最优化的解： $_{k-1}^{\ \ 0}\textrm{g}_{k}^{*\nu }=\mathop {argmin}_{_{k-1}^{0}\textrm{g}_{k}^{\nu}}\sum_{i}^{n_{d}}\rho _{h}\left ( \textrm{e}_{i}^{\top }\left ( _{k-1}^{\ \0}\textrm{g}_{k} \right ) \sum_{p}^{-1}\textrm{e}_{i}\left ( _{k-1}^{\ \ 0}\textrm{g}_{k} \right )\right )$ ，（11）

$n_{d}$ 为在 $k-1$ 到 $k$ 帧3D-2D可见的动态物体对应点，物体运动由 $_{k-1}^{\ \ 0}\textrm{H}_{k} = _{}^{0}\textrm{X}_{k} \ _{k-1}^{\ \ 0}\textrm{G}_{k}$ 恢复。

3.2.3 加入光流估计：

对于相机位姿估计，（7）的误差函数被重新定义为： $\textrm{e}_{i}\left ( _{}^{0}\textrm{X}_{k},_{}^{I_{k}}\phi \right )=_{}^{I_{k-1}}\textrm{p}_{k-1}^{i}+_{}^{I_{k}}\phi_{i}-\pi \left ( _{}^{0}\textrm{X}_{k}^{-1} \ _{}^{0}\textrm{m}_{k-1}^{i} \right )$ ，（12）

将上面公式中 $SE\left ( 3 \right )$ 李代数化，最小化损失函数获得最优解： $\left \{ \textrm{x}_{k}^{*\nu },_{}^{k}\Phi_{k}^{*} \right \} = \mathop {argmin}_{\left \{ \textrm{x}_{k}^{\nu },_{}^{k}\Phi_{k} \right \}} \sum_{i}^{n_{b}}\left \{ \rho _{h}\left ( \textrm{e}_{i}^{\top }\left ( _{}^{I_{k}}\phi _{}^{i} \right )\sum_{\phi}^{-1} \textrm{e}_{i}\left ( _{}^{I_{k}}\phi _{}^{i} \right ) \right )+ \rho _{h} \left ( \textrm{e}_{i}^{\top }\left ( _{}^{0}\textrm{x}_{k},_{}^{I_{k}}\phi _{}^{i} \right ) \sum_{p}^{-1} \textrm{e}_{i}\left ( _{}^{0}\textrm{x}_{k},_{}^{I_{k}}\phi _{}^{i} \right )\right )\right \}$ ，（13）

其中： $\rho _{h}\left ( \textrm{e}_{i}^{\top }\left ( _{}^{I_{k}}\phi _{}^{i} \right )\sum_{\phi}^{-1} \textrm{e}_{i}\left ( _{}^{I_{k}}\phi _{}^{i} \right ) \right )$ 是带有 $\textrm{e}_{i}\left ( _{}^{I_{k}}\phi _{}^{i} \right ) = _{}^{I_{k}}\widehat{\phi }_{}^{i} - _{}^{I_{k}}\phi _{}^{i}$ ，（14）的正则项。

这里 $_{}^{I_{k}}\widehat{\Phi}_{}^{i}=\left \{ _{}^{I_{k}}\widehat{\phi }_{}^{i} | i\in\mathbb{M},k\in\mathbb{J}\right \}$ 是通过经典方法或基于学习的方法得到的初始光流， $\sum_{\phi}$ 是相关的协方差矩阵。

类似的，（11）中物体运动的代价函数结合光流为： $\left \{ _{k-1}^{0}\textrm{g}_{k}^{*\nu },_{}^{k}\Phi_{k}^{*} \right \} = \mathop {argmin}_{\left \{ _{k-1}^{0}\textrm{g}_{k}^{\nu },_{}^{k}\Phi_{k} \right \}} \sum_{i}^{n_{d}}\left \{ \rho _{h}\left ( \textrm{e}_{i}^{\top }\left ( _{}^{I_{k}}\phi _{}^{i} \right )\sum_{\phi}^{-1} \textrm{e}_{i}\left ( _{}^{I_{k}}\phi _{}^{i} \right ) \right )+ \rho _{h} \left ( \textrm{e}_{i}^{\top }\left ( _{k-1}^{\ \ 0}\textrm{g}_{k},_{}^{I_{k}}\phi _{}^{i} \right ) \sum_{p}^{-1} \textrm{e}_{i}\left ( _{k-1}^{\ \ 0}\textrm{g}_{k},_{}^{I_{k}}\phi _{}^{i} \right )\right )\right \}$ ，（15）

3.3 图优化

我们将动态SLAM问题建模为一个因子图，如下图所示

3D点测量模型误差被定义为： $\textrm{e}_{i,k}\left ( _{}^{0}\textrm{X}_{k} , \textrm{m}_{k}^{i}\right )=_{}^{0}\textrm{X}_{k}^{-1} \ _{}^{0}\textrm{m}_{k}^{i}-\textrm{z}_{k}^{i} ,\textrm{z}=\left \{ \textrm{z}_{k}^{i} | i\in\mathbb{M} , k\in\mathbb{J}\right \}$ （16） $\textrm{z}$ 是在所有时间节点的所有3D点测量值的集合， $n_{z},\textrm{z}_{k}^{i} \in \mathbb{R}_{}^{3}$ ，由图3中白色圆表示。

视觉里程计误差模型为： $\textrm{e}_{k}\left ( _{}^{0}\textrm{X}_{k-1} , _{}^{0}\textrm{X}_{k} \right ) = \left ( _{}^{0}\textrm{X}_{k-1}^{-1} \ _{}^{0}\textrm{X}_{k}\right )_{}^{-1} \ _{k-1}^{X_{k-1}}\textrm{T}_{k},\textrm{T}=\left \{ _{k-1}^{X_{k-1}}\textrm{T}_{k} | k \in \mathbb{J}\right \}$ （17）， $_{k-1}^{X_{k-1}}\textrm{T}_{k} \in SE\left ( 3 \right )$ 为里程测量，由图3中橙色圆表示。

动态物体上点的运动模型误差为： $\textrm{e}_{i,l,k}\left ( _{}^{0}\textrm{m}_{k}^{i} , _{k-1}^{\ \0}\text{H}_{k}^{l} , _{}^{0}\textrm{m}_{k-1}^{i}\right ) = _{}^{0}\textrm{m}_{k}^{i} - _{k-1}^{\ \0}\text{H}_{k}^{l} \ _{}^{0}\textrm{m}_{k-1}^{i}$ （18），对被检测刚体上所有点的运动由与（6）一样的 $_{k-1}^{\ \0}\text{H}_{k}^{l} \in SE\left ( 3 \right )$ 表示，由图3中粉色圆表示。

受摄像机帧率和控制相对较大物体(车辆)运动和防止其运动突然变化的物理定律的驱动，我们引入平滑运动因子来最小化连续物体运动的变化，误差为: $\textrm{e}_{l,k}\left ( _{k-2}^{\ \ 0}\textrm{H}_{k-1}^{l} , _{k-1}^{\ \ 0}\textrm{H}_{k}^{l}\right ) = {_{k-2}^{\ \ 0}\textrm{H}_{k-1}^{l}}_{}^{-1} \ _{k-1}^{\ \ 0}\textrm{H}_{k}^{l}$ （19），由图3中青色圆表示。

$\theta_{M}=\left \{ _{}^{0}\textrm{m}_{k}^{i} | i \in \mathbb{M} , k \in \mathbb{J} \right \}$ ：所有3D点集合；

$\theta_{X}=\left \{ _{}^{0}\textrm{x}_{k}^{\nu} | k \in \mathbb{J} \right \}$ ：所有相机位姿集合；

将物体运动李代数化： $_{k-1}^{\ \0}\textrm{H}_{k}^{l} = exp\left ( _{k-1}^{\ \0}\textrm{h}_{k}^{l} \right )$ （20），则 $\theta_{H}=\left \{ _{k-1}^{\ \0}\textrm{h}_{k}^{l\nu} | k \in \mathbb{J} , l \in \varphi \right \}$ 定义为物体运动集合， $_{k-1}^{\ \0}\textrm{h}_{k}^{l\nu} \in \mathbb{R}_{}^{6}$ ， $\varphi$ 为运动物体标签集合。

设 $\theta = \theta_{X}\bigcup \theta_{M}\bigcup \theta_{H}$ 为图中所有节点，将 $\textrm{X},\textrm{H} \in SE\left ( 3 \right )$ 李代数化（将（8）代入到（16）和（17），将（20）代入到（18）和（19）），最后，最小二乘法代价函数为：

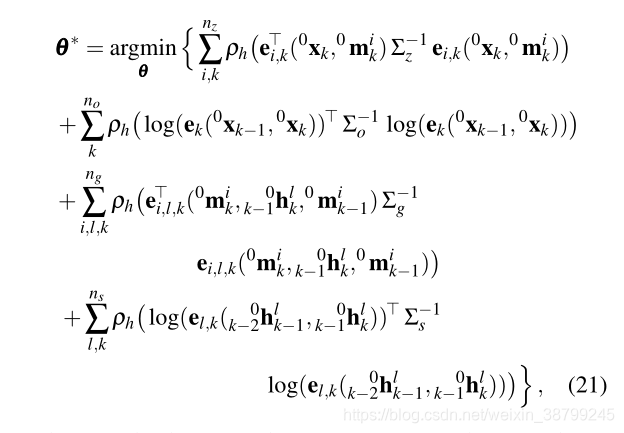
其中Σz为三维点测量噪声协方差矩阵，Σo为测程噪声协方差矩阵，Σg为3D物体运动因子总数的运动噪声协方差矩阵，Σs为平滑运动协方差矩阵，ns为平滑运动因子总数。

采用列文伯格-马夸尔特求解（21）

4 系统

整个系统概述如图4所示。该系统主要由图像预处理、跟踪和建图三个部分组成

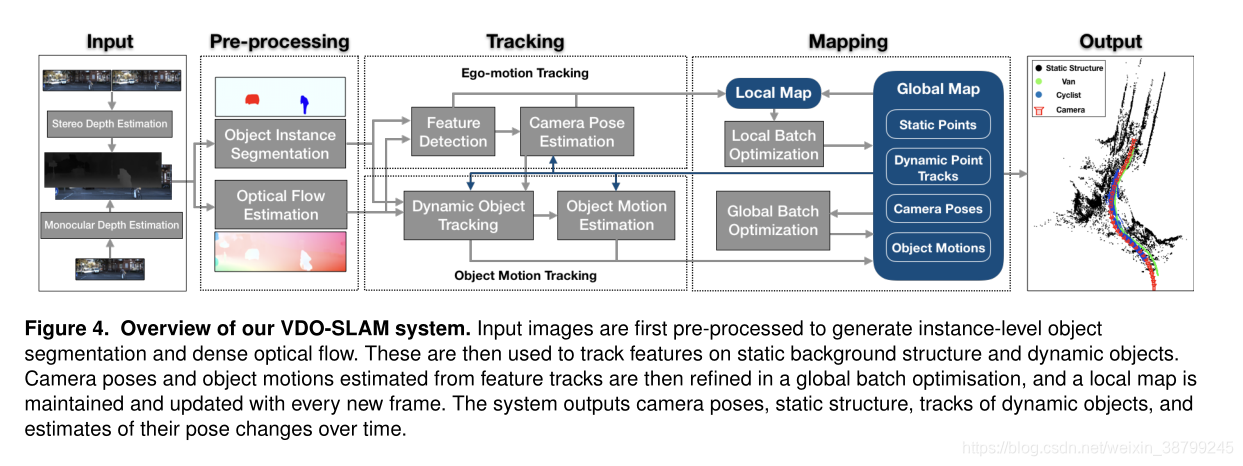
系统的输入是立体或RGB-D图像。对于立体图像，作为第一步，我们提取深度信息，生成深度图，所得数据作为RGB-D处理。

4.1 预处理

这个模块需要完成两个具有挑战性的方面。一是对静态背景和目标进行分离，二是保证对动态目标的长期跟踪。

为了实现这一目标，我们利用计算机视觉技术在实例级语义分割和密集光流估计方面的最新进展，以确保有效的目标运动分割和鲁棒的目标跟踪。

4.1.1 物体实列分割：

实例级语义分割用于分割和识别场景中可能移动的对象。语义信息在分离静态和移动物体点的过程中是一个重要的优先条件，例如，建筑物和道路总是静态的，但汽车可以是静态的或动态的。实例分割有助于将语义前景进一步划分为不同的实例Mask，便于跟踪每个单独的对象。此外，分割掩模提供了一个“精确的”目标体边界，以确保对目标上的点进行鲁棒跟踪。

4.1.2 光流估计：

利用密集光流可以最大化跟踪运动目标上点的数量。大多数运动目标只占图像的一小部分。因此，使用稀疏特征匹配不能保证鲁棒性和长期的特征跟踪。我们的方法利用了密集光流，通过对语义mask内的所有点进行采样来显著增加（对于运动）目标（提取出的）点的数量。密集光流还可以通过分配给目标mask每个点的唯一标识符来持续地跟踪多个位姿。在语义分割失败的情况下，（DVO-SLAM）可以恢复目标mask;而使用稀疏特征匹配很难实现这种任务。

4.2 跟踪

跟踪包括两个模块;摄像机的自运动跟踪包括特征检测和摄像机姿态估计子模块，目标运动跟踪包括动态目标跟踪和目标运动估计子模块。

4.2.1 特征检测：

为了实现快速的相机位姿估计，我们检测一组稀疏的角点特征并利用光流对其进行跟踪。在每一帧中，只有拟合相机运动估计的内点才被保存到地图中，用于跟踪下一帧的对应（点）。如果跟踪到的内点的数量低于某一阈值，系统就会检测并添加新的特征。在静态背景下检测到的稀疏特征中，图像区域不包括被分割的位姿。

4.2.2 相机位姿估计：

对于所有检测到的3D-2D对应静态点，DVO-SLAM使用公式(13)可以计算得到相机位姿。为了保证估计的鲁棒性，系统采用运动模型生成方法对数据进行初始化。具体说来，该方法基于重投影误差生成了两个模型，并对两个模型的内值进行了比较。一个模型是通过计算相机之前的运动生成的，而另一个模型是通过使用RANSAC的P3P ((Ke and Roumeliotis (2017))算法计算新的运动变换生成的。系统会选择产生较多内点的运动模型进行初始化操作。

4.2.3 动态物体追踪：

运动目标的跟踪过程分为两个步骤。第一步将分割的目标分为静态目标和动态目标。第二步通过连续的帧来关联动态目标。

实例级目标分割允许我们从背景中分离目标。虽然算法有能力对所有的分割目标估计其运动，动态目标的有效识别可以有助于降低系统的计算成本。这是基于场景流估计实现的。具体来说，在获得相机位姿后，描述三维点在k-1到k帧之间运动的场景流向量可以被计算得到：

$\textrm{f}_{k}^{i}=_{}^{0}\textrm{m}_{k-1}^{i}-_{}^{0}\textrm{m}_{k}^{i}=_{}^{0}\textrm{m}_{k-1}^{i}-_{}^{0}\textrm{X}_{k} \ _{}^{X_{k}}\textrm{m}_{k}^{i}$ ，（22）

与光流法不同，场景流(理想情况下仅由场景移动引起)可以直接决定某些结构是否有过移动。理想情况下，对应于所有静态三维点的场景流向量的大小应该为零。然而，在深度和匹配方面的噪声或错误会使真实场景中的情况复杂化。为了稳健地处理这个问题，我们会对每个目标上的所有样本点计算它们的场景流大小。如果场景中某些点的场景流数值大于预先设定的阈值，则认为该点是运动的。在本系统进行的所有实验中，这个阈值都被设置为0.12。如果“动态”点的比例高于某一水平(所有点数的30%)，则该目标会被识别为是运动的，否则该目标为静止的。如前文所述，（设置）阈值是用于识别一个位姿是否是动态的，为了（使结果）更加保守，系统可以灵活地将一个静态位姿建模为动态位姿，并每个时间步长对其估计出一个（大小为）零的运动。然而，如果进行相反的处理，则会降低系统的性能。

实例级位姿分割只能提供单个图像目标标签，然后需要随时间在帧之间跟踪目标以及它们的运动模型。我们建议使用光流法来关联帧之间的点标签。一个点标签与采样点的唯一目标标识符相同。我们保持一个有限的跟踪标签集。当探测到更多运动的目标时，标签集的元素数量就会增加。静态位姿和背景使用 $l=0$ 标记。

理想情况下，对于k帧中的每个被检测位姿，其所有点的标签都应该唯一地与k-1帧中的对应标签对齐。但在实际应用中，这会受到噪声、图像边界和遮挡的影响。为了克服这个问题，我们给所有的点都贴上了标签，当这些点对应起来时就会使标签的数目达到最大。对于一个动态目标而言，如果它前一帧中最频繁的标签为0，这意味着该目标（在这一帧才）开始移动，出现在场景的边界上，或者从遮挡中重新出现。在这种情况下，该位姿会被分配一个新的跟踪标签。

4.2.4 物体运动估计：

如上文所述，（运动）目标在场景中通常是小范围出现的，很难得到足够的稀疏特征来稳健地跟踪和估计目标的运动。我们对所有位姿mask内的第三个点进行了采样，并在图像帧之间对它们进行跟踪。与相机位姿估计相似，只有内点会被保存进地图中并用于下一帧的跟踪。当跟踪的目标点减少到一定水平以下时，会对目标进行采样并添加新的目标点。我们采用了4.2.2节中讨论的方法来生成初始目标运动模型。

4.3 建图

在地图模块中，系统会构造并维护一个全局地图。同时，系统会从全局地图中提取出一个基于当前时间步长和前一个时间步长窗口的局部地图。两个地图都是通过批量优化过程更新的。

4.3.1 局部批量优化：

我们的系统会维护和更新一个局部地图。局部批量优化的目标是确保将精确的相机位姿估计提供给全局批量优化。相机位姿估计对目标运动估计的精度和算法的整体性能有很大的影响。局部地图是使用一个固定大小的包含最后一帧信息的滑动窗口构建的。局部地图会共享一些公共信息:这会造成不同窗口之间的重叠。我们选择只在窗口大小范围内局部优化相机位姿和静态结构，因为局部优化动态结构不会给优化带来任何好处，除非在窗口内假设存在硬约束(例如目标的恒定运动)。但是，如果需要的话，系统能够在局部地图中合并静态和动态结构。当一个局部地图以类似的方式构造时，因子图优化将执行来细化局部地图中的所有变量，然后将它们在全局地图中进行更新。

4.3.2 全局批量优化：

跟踪模块的输出和局部批量优化包含了相机位姿、目标运动和内点结构。它们被保存在一个全局地图中，这个全局地图是由之前的所有时间帧构建的，并且随着每一个新的时间帧的加入不断更新。在处理完所有输入帧后，系统会基于全局地图构造因子图。为了有效地获得时间约束，系统在因子图中只添加被跟踪超过3个实例的点。该图被表述为如3.3节中描述的优化问题。优化结果将作为整个系统的输出。

4.3.3 从地图到跟踪:

维护地图可以为跟踪模块估算当前状态时提供历史信息，如图4所示，蓝色箭头从全局地图指向系统跟踪模块的多个组件。利用最后一帧的内点可以跟踪当前帧中的对应点并估计相机位姿和目标运动。最后的相机和目标运动也可能作为先验模型来初始化4.2.2和4.2.4节中所述的当前估计问题。此外，在语义位姿分割失败导致“间接遮挡”的情况下，通过利用之前分割的mask，（运动）目标（上提取出的）点可以帮助（系统实现）跨帧关联语义mask，以确保对目标的鲁棒跟踪。

VDO-SLAM 基于视觉的动态感知SLAM系统