一、概述

这个函数说实话有点麻烦，因为会用到NANOFLANN库。刚开始我一头扎进这个nanoflann.h头文件里，但是越是深入, 就越会发现人类的能力是有极限的，现在想来还是自己太狂妄了。

二、kd树

言归正传，NANOFLANN库主要作用是构建kd树，方便查询数据。

2.1 树结构

把集合中的数据按分支关系排列就构成树结构。理解上应该是和聚类差不多的概念，比如在集合{1,25,30,35,60,65}里查找65，单个元素为一类，要是从大到小排列还好，从小到大的话查找时间就直接取决于元素个数N=5。而把元素排列为{1}-{30}-{25,35}和{1}-{60}-{65}两棵子树，查找时间取决于高度h=3。
结论：一个好的树结构能有效提高查找效率。

一维空间使用平衡二叉树的搜索效率应该是最高的，平衡二叉树要求左右子树的高度差不大于1。

2.2 kd树构建

k维空间通过对每维数据切分来得到树结构，维度选择顺序也影响效率[1]，一般采用交替切分的方式，第一轮选切分维度需要计算方差[2]。分割的对象称为超平面，理想的超平面是对应维度的中位数。直到最大的叶子节点尺寸小于或等于阈值（leaf_max_size）。
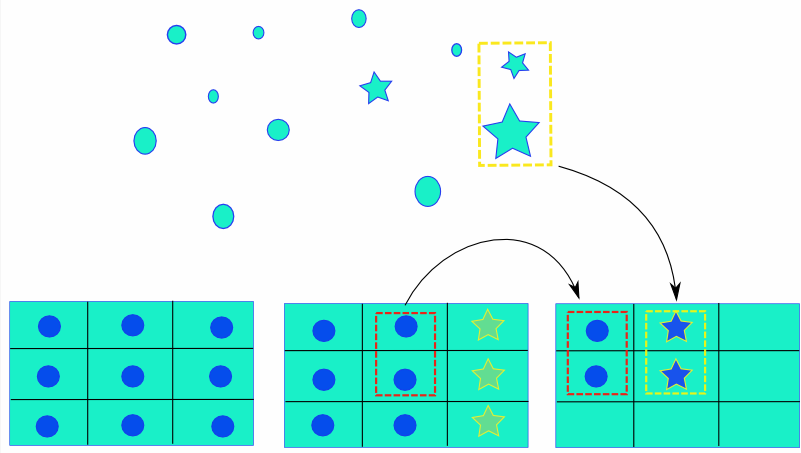
对K维空间数据进行切分就构成kd树（k-dimensional tree）。图像参考[1]。

2.3 最近邻搜索

对二维空间而言，给定点p，查询集合中与其距离最近点的过程即为最近邻搜索（Nearest Neighbour，NN）。按照问题的复杂程度，可以分解为两个方面 1-NN与 k-NN，分别表示距离搜索点最近的一个点以及最近的k个点[1]。

1-NN大致流程

(1) 二叉法查找到最近叶子节点，保存最近点和最小距离；
(2) 回溯查找到父节点，在搜索点处以最小距离画圆，圆与其父节点所在超平面相交，则(3)，否则(4)；
(3) 进入对应子树查找到叶子节点，保存最近点和最小距离，执行(4)；
(4) 一直回溯到根节点，圆与根节点所在超平面不相交，则搜索结束，返回最近邻点和最小距离。

详细解释推荐查看[3]。

k-NN与1-NN的区别在于k-NN保存的是最近邻点集和点集的最大距离（FLANN中称为worest distance）。和聚类真的好像。

2.4 FLANN和NANOFLANN

FLANN（Fast Library for Approximate Nearest Neighbors），翻译成中文叫做快速近似最近邻搜索库。
ANN属于对最近邻搜索（NN）的改进，通过将最小距离除以 大于1的系数，使过程(3)能更快地筛选节点。这种方式（ANN）能使 NN的查询速度提高10-100倍。

nanoflann是对原始flann库的改进，具体优点参考[4]。

三、makeNN

以下是函数注释。

void CoarseInitializer::makeNN()
{const float NNDistFactor=0.05;// 第一个参数为距离, 第二个是特征点集, 第三个是维数typedef nanoflann::KDTreeSingleIndexAdaptor<nanoflann::L2_Simple_Adaptor<float, FLANNPointcloud> ,FLANNPointcloud,2> KDTree;// build indices构建索引FLANNPointcloud pcs[PYR_LEVELS];KDTree* indexes[PYR_LEVELS];//遍历金字塔，为每层二维点集建立一个KDTree索引for(int i=0;i<pyrLevelsUsed;i++){pcs[i] = FLANNPointcloud(numPoints[i], points[i]);//初始化indexes[i] = new KDTree(2, pcs[i], nanoflann::KDTreeSingleIndexAdaptorParams(5) );//为每层开辟kd-tree空间indexes[i]->buildIndex();//创建最近邻搜索索引}const int nn=10;//就是k-NN的k// find NN & parents遍历金字塔for(int lvl=0;lvl<pyrLevelsUsed;lvl++){Pnt* pts = points[lvl];//第lvl层特征点集int npts = numPoints[lvl];//点集尺寸int ret_index[nn];//搜索到的最近邻点集float ret_dist[nn];//点集的最大距离nanoflann::KNNResultSet<float, int, int> resultSet(nn);//当前层搜索结果nanoflann::KNNResultSet<float, int, int> resultSet1(1);////遍历所有特征点for(int i=0;i<npts;i++){//resultSet.init(pts[i].neighbours, pts[i].neighboursDist );resultSet.init(ret_index, ret_dist);//初始化Vec2f pt = Vec2f(pts[i].u,pts[i].v);indexes[lvl]->findNeighbors(resultSet, (float*)&pt, nanoflann::SearchParams());//使用建立的KDtree, 来查询最近邻int myidx=0;float sumDF = 0;//计算距离和for(int k=0;k<nn;k++){pts[i].neighbours[myidx]=ret_index[k];float df = expf(-ret_dist[k]*NNDistFactor);//计算距离的指数sumDF += df;pts[i].neighboursDist[myidx]=df;assert(ret_index[k]>=0 && ret_index[k] < npts);myidx++;}for(int k=0;k<nn;k++)pts[i].neighboursDist[k] *= 10/sumDF;//距离归10化if(lvl < pyrLevelsUsed-1 ){resultSet1.init(ret_index, ret_dist);//初始化pt = pt*0.5f-Vec2f(0.25f,0.25f);//转换到高一层indexes[lvl+1]->findNeighbors(resultSet1, (float*)&pt, nanoflann::SearchParams());//在高层查询最近邻1-NNpts[i].parent = ret_index[0];//保存高层搜索到的最近邻索引pts[i].parentDist = expf(-ret_dist[0]*NNDistFactor);//保存距离assert(ret_index[0]>=0 && ret_index[0] < numPoints[lvl+1]);}else{pts[i].parent = -1;//最高层pts[i].parentDist = -1;}}}for(int i=0;i<pyrLevelsUsed;i++)delete indexes[i];
}

更新

又重新学了一下FLANN相关的kdtree和最近邻搜索。
参考了DSO的makeNN函数，重新考虑了一下上面的例子，用程序作为学习成果分享一下。

#include <iostream>
#include <vector>
#include <math.h>
#include "Eigen/Core"
#include "nanoflann.h"
using namespace std;//参考DSO的CoarseInitializer.h里的struct FLANNPointcloud的写法
struct Pointcloud
{typedef std::vector<vector<int>> pts;inline Pointcloud(int n, pts p) :  num(n), points(p) {}int num;pts points;//点集// 返回数据点的数目inline size_t kdtree_get_point_count() const { return num; }// 返回欧式距离inline float kdtree_distance(const float *p1, const size_t idx_p2,size_t ) const{const float d0=p1[0]-points[idx_p2][0];const float d1=p1[1]-points[idx_p2][1];return sqrt(d0*d0+d1*d1);}inline float kdtree_get_pt(const size_t idx, int dim) const{if (dim==0) return points[idx][0];else return points[idx][1];}template <class BBOX>bool kdtree_get_bbox(BBOX& ) const { return false; }
};int main()
{//准备数据vector<vector<int>> t_data = {{30,40},{5,25},{35,45},{10,12},{70,70},{50,30}};vector<int> test = {6,12};int k = t_data[0].size();//样本维度int num = t_data.size();//样本数量// 第一个参数为distance, 第二个是datasetadaptor, 第三个是维数typedef nanoflann::KDTreeSingleIndexAdaptor<nanoflann::L2_Simple_Adaptor<float, Pointcloud>,Pointcloud, 2> KDTree;int neighbours;//最近点float neighboursDist;   //最近点的距离KDTree* indexes; // 点云建立KDtreePointcloud pcs = Pointcloud(num, t_data); indexes = new KDTree(2, pcs, nanoflann::KDTreeSingleIndexAdaptorParams(3));indexes->buildIndex();const int nn=1;int ret_index[nn];  // 搜索到的临近点float ret_dist[nn]; // 搜索到点的距离nanoflann::KNNResultSet<float, int, int> resultSet1(1);Eigen::Matrix<float,2,1> pt = Eigen::Matrix<float,2,1>(test[0],test[1]); // 当前点for(int i=0;i<num;i++){resultSet1.init(ret_index, ret_dist);// 使用建立的KDtree, 来查询最近邻indexes->findNeighbors(resultSet1, (float*)&pt, nanoflann::SearchParams());neighbours=ret_index[0]; // 最近的索引float df = ret_dist[0]; neighboursDist=df;}return 0;
}

总结

这个函数想通过看程序来理解真的有难度，我只能把理论先看一遍，至于nanoflann库的实现只能以后再说了。

参考资料

[1] http://www.whudj.cn/?p=920
[2] https://zhuanlan.zhihu.com/p/53826008
[3] https://blog.csdn.net/app_12062011/article/details/51986805
[4] https://www.5axxw.com/wiki/content/g4pz76