目录
- 是什么?
- 基本概念总结
- 1.相关名词
- 2.反射系数
- 3.传输线阻抗公式
- 图怎么看?
- 史密斯圆图知识点
- 史密斯圆图使用?
- 1.ADS软件安装
- 2.史密斯圆图仿真
- 结语
是什么?
该图表是由菲利普·史密斯(Phillip Smith)于1939年发明的。
简单的说:类似于数学用表一样,通过查找,知道反射系数的数值。主要用来解决传输线问题,做高频电路之间的阻抗匹配用的。
基本概念总结
1.相关名词
阻抗:电阻、电感的感抗、电容的容抗三种类型的复物,复合后统称“阻抗”。写成数学公式即是:Z= R+j(ωL–1/(ωC))。其中R为电阻,ωL为感抗,1/(ωC)为容抗。
(1)如果(ωL–1/ωC)>0,称为“感性负载”;
(2)反之,如果(ωL–1/ωC)<0,称为“容性负载”。
例1:在RLC串联电路中,交流电源电压U=220V,频率f=50Hz,R=30 Ω,L=445mH,C=32 mF。

2.反射系数
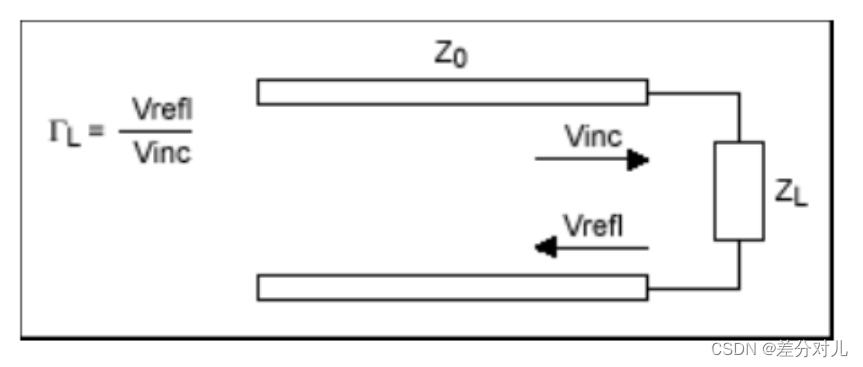
反射系数是一个描述在传输介质中因为阻抗的不连续造成有多少电磁波被反射的参数。它等于反射波与入射波的振幅比,两者也可以相量表示。
当中的Γ代表其线路的反射系数(reflection coefficient),我们知道反射系数定义为反射波电压与入射波电压之比:
公式为: Γ Γ Γ= V r e f l V i n C \frac{V_{refl}}{V_{inC}} VinCVrefl= Z L − Z 0 Z L + Z 0 \frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}} ZL+Z0ZL−Z0
3.传输线阻抗公式
在传输线理论中,当一段特征阻抗为 Z 0 Z_{0} Z0传输线终端连接了一个阻抗为 Z L Z_{L} ZL的负载时,看向这段传输线的输入阻抗 Z i n Z_{in} Zin将不再是 Z 0 Z_{0} Z0。
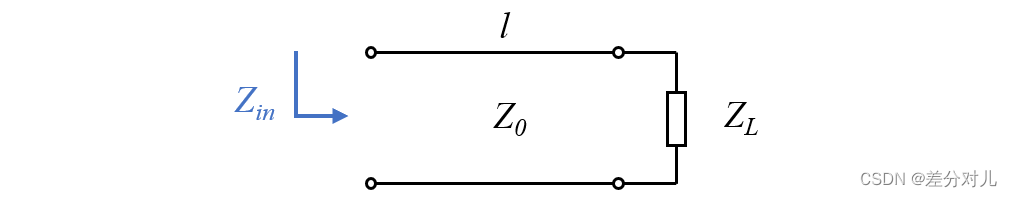
传输线阻抗方程 (Transmission Line Impedance Equation) 就是计算此时传输线的输入阻抗 Z i n Z_{in} Zin的公式,它是RF系统中求解阻抗匹配问题的一个重要公式。传输线阻抗方程的最终形式如下:
Z i n Z_{in} Zin= Z 0 Z_{0} Z0· Z L + j Z 0 t a n ( β l ) Z 0 + j Z L t a n ( β l ) \frac{Z_{L}+jZ_{0}tan(βl)}{Z_{0}+jZ_{L}tan(βl)} Z0+jZLtan(βl)ZL+jZ0tan(βl)
其中,β = 2π/λ,λ为在传输线上传播的信号波长,l为传输线的长度。
特殊情况:当l=λ/4时,上述公式为: Z i n Z_{in} Zin= Z 0 2 Z L \frac{Z_{0}^2}{Z_{L}} ZLZ02
因此,我们只需要让传输线与阻抗之间的四分之一波长变换器的阻抗按上式取值,即可使实现将实数负载阻抗匹配至传输线。
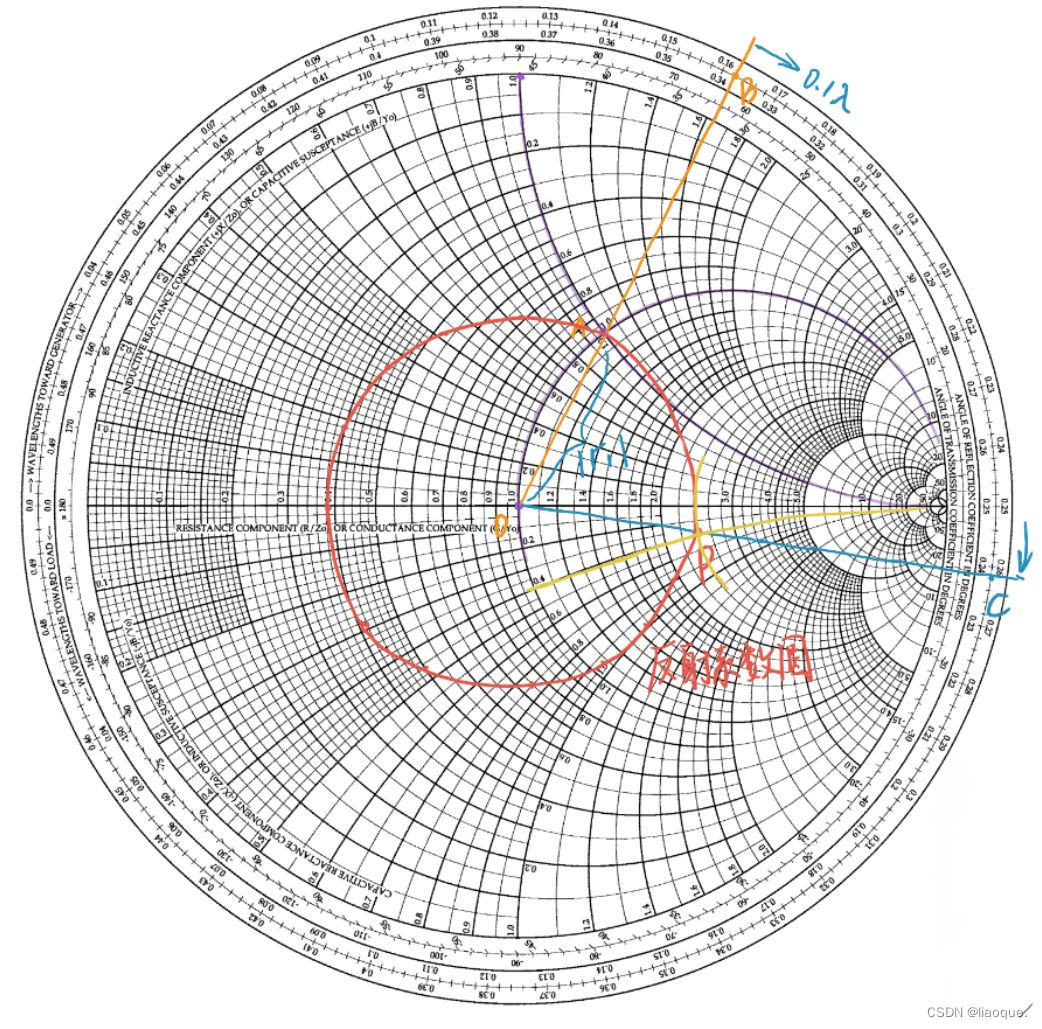
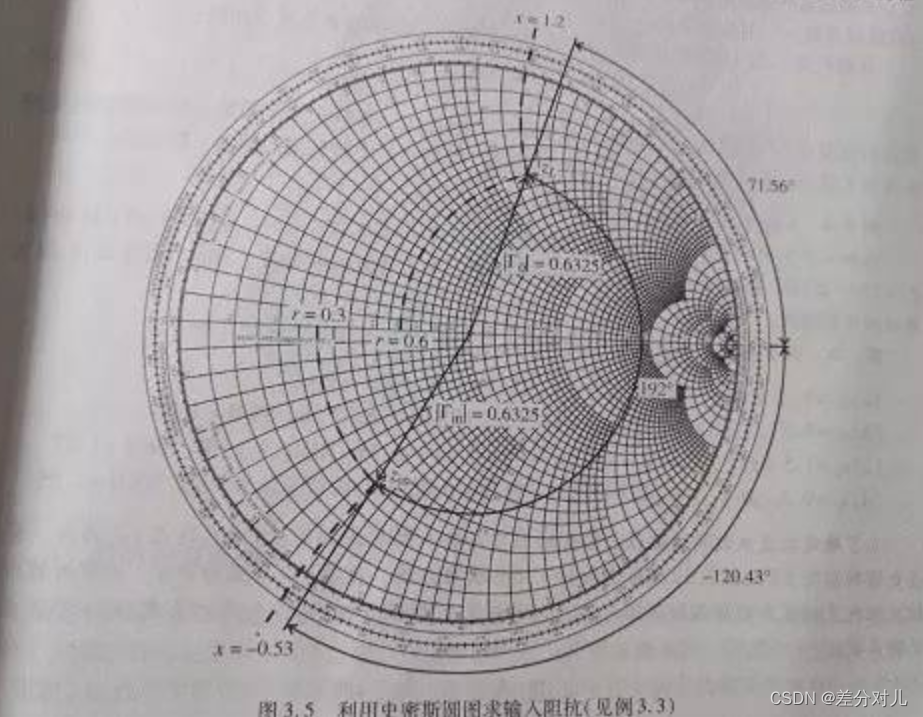
图怎么看?
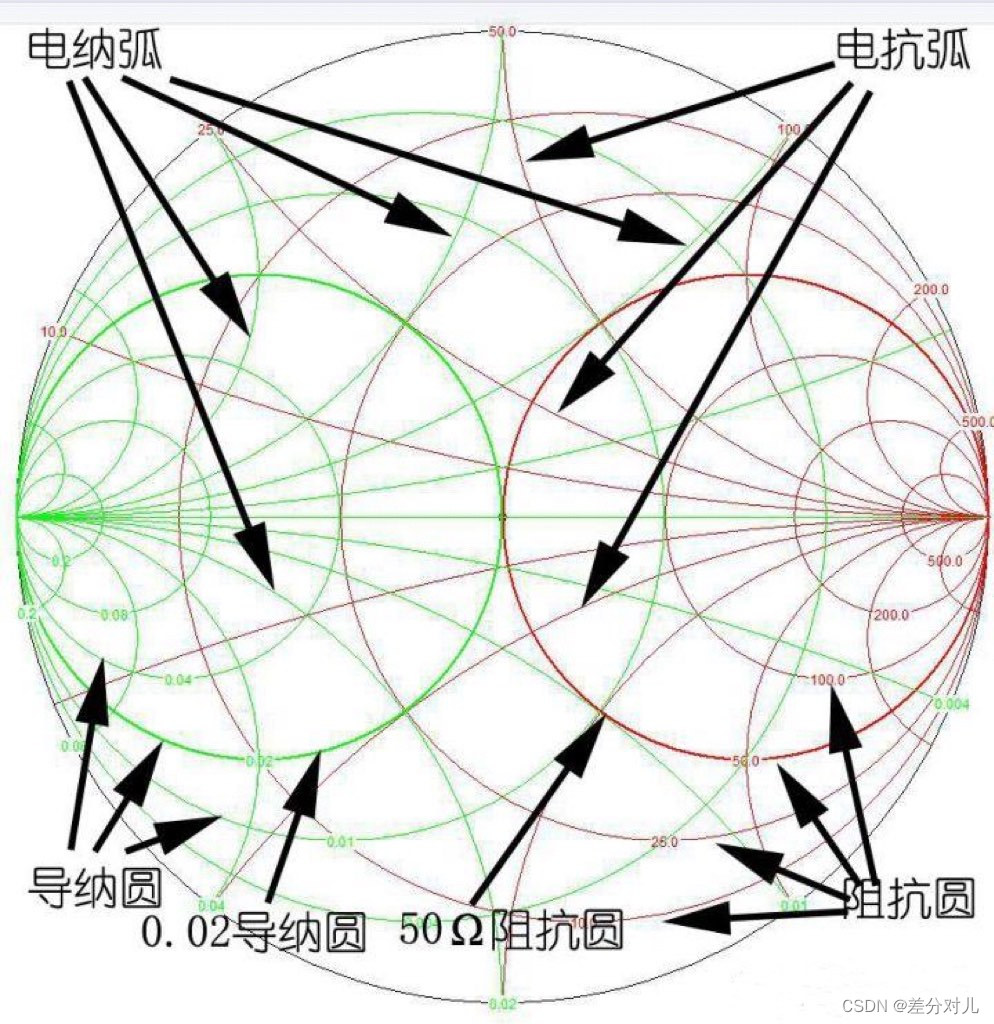
归一化阻抗值举例
100Ω-j50Ω的点在哪儿?
第一步,计算归一化实部阻抗值为100Ω/50Ω=2;归一化阻抗虚部为-50Ω/50Ω=-1。
第二步,在等电阻线上,找到归一化阻抗值为2的阻抗圆。
第三步,沿着归一化阻抗值为2的阻抗圆下旋,转到-1那个电抗弧上。
第四步,做个记号!我标的是X。
归一化导纳值举例
0.04S+j0.02S的点在哪儿?
第一步,计算归一化实部导纳值为0.04S/0.02S=2;归一化虚部导纳值为0.02S/0.02S=1。
第二步,在等电阻线上,找到归一化导纳值为2的导纳圆。
第三步,沿着归一化导纳值为2的导纳圆上旋,转到导纳值为1的那个电纳弧上。
第四步,做个记号!即Z。
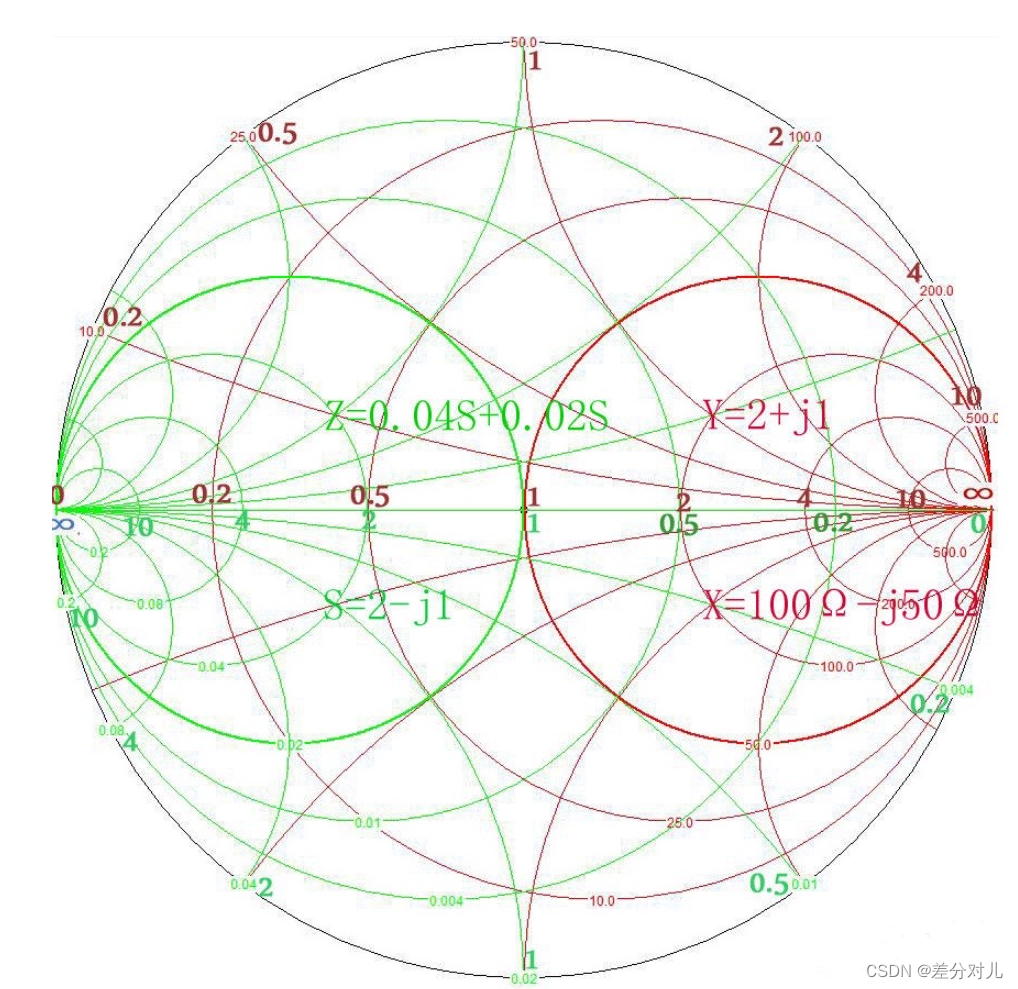
史密斯圆图知识点
1.图上重要的5个点
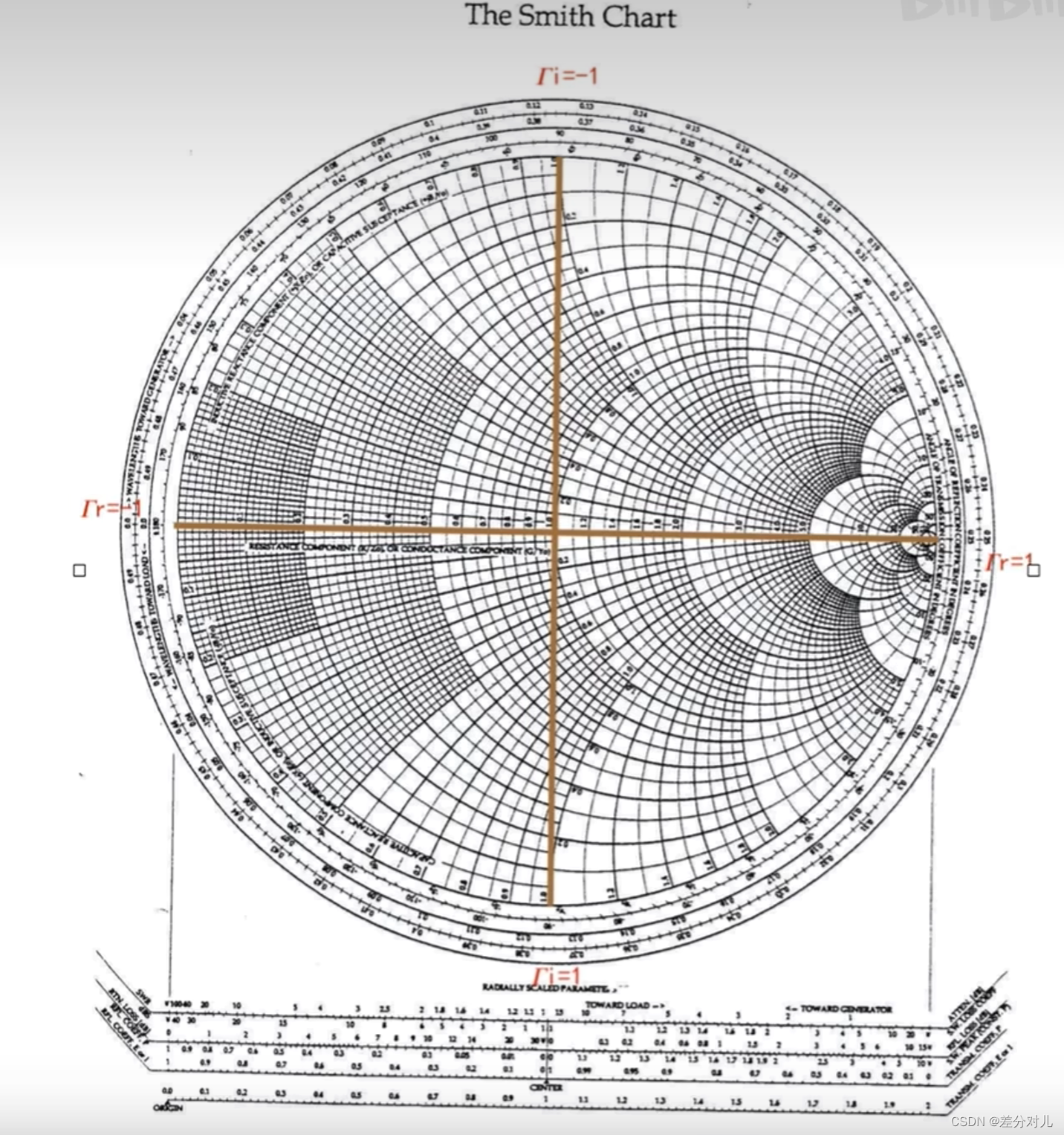
z L z_L zL= Z L Z 0 \frac{Z_{L}}{Z_{0}} Z0ZL= 1 + ∣ Γ r ∣ + j Γ i 1 − ∣ Γ r ∣ − j Γ i \frac{1+|Γ_r|+jΓ_i}{1-|Γ_r|-jΓ_i} 1−∣Γr∣−jΓi1+∣Γr∣+jΓi
z L z_L zL(right)= 1 + 1 1 − 1 \frac{1+1}{1-1} 1−11+1= ∞ ∞ ∞
z L z_L zL(left)= 1 − 1 1 + 1 \frac{1-1}{1+1} 1+11−1= 0 0 0
z L z_L zL(top)= 1 + j 1 − j \frac{1+j}{1-j} 1−j1+j= j j j
z L z_L zL(bottom)= 1 − j 1 + j \frac{1-j}{1+j} 1+j1−j= − j -j −j
z L z_L zL(0)= 1 1 \frac{1}{1} 11= 1 1 1
史密斯圆图使用?
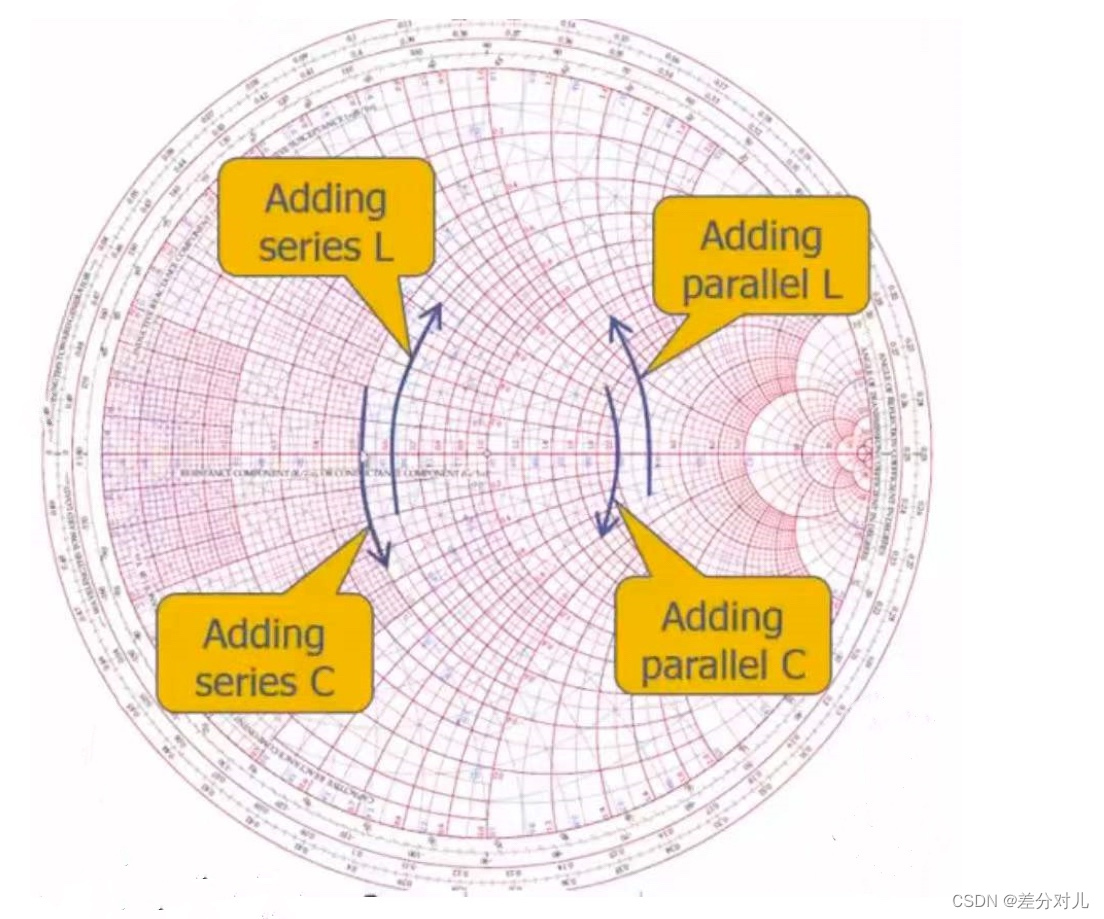
2.我们常说的口诀:上感下容,左串右并,具体的其实体现为:
串联电感,沿电抗图的顺时针方向移动;
串联电容,沿电抗图的逆时针方向移动
并联电感,沿导纳图的逆时针方向移动;
并联电容,沿导纳图的顺时针方向移动
1.ADS软件安装
1.首先从网站下载安装软件,并点击应用程序

2.进入安装向导
注意:尽量一次安装成功,否则注册表若不删除干净,第六项的EEsof License安装步骤会跳过。
3.安装完成后得到两个文件夹

4.将下载过来的文件中的下图文件夹复制。

拷贝到安装好的bin文件覆盖。
将下载过来的文件中的license.lic复制。
粘贴license.lic,到安装目录下。
将下载过来的文件中的ADS2020复制。
粘贴到安装文件下如下图所示。
注意:该步骤需要复制bin文件夹,license.lic,ADS2020文件夹中的文件。
5.环境变量安装
我的电脑->属性->高级系统设置->环境变量
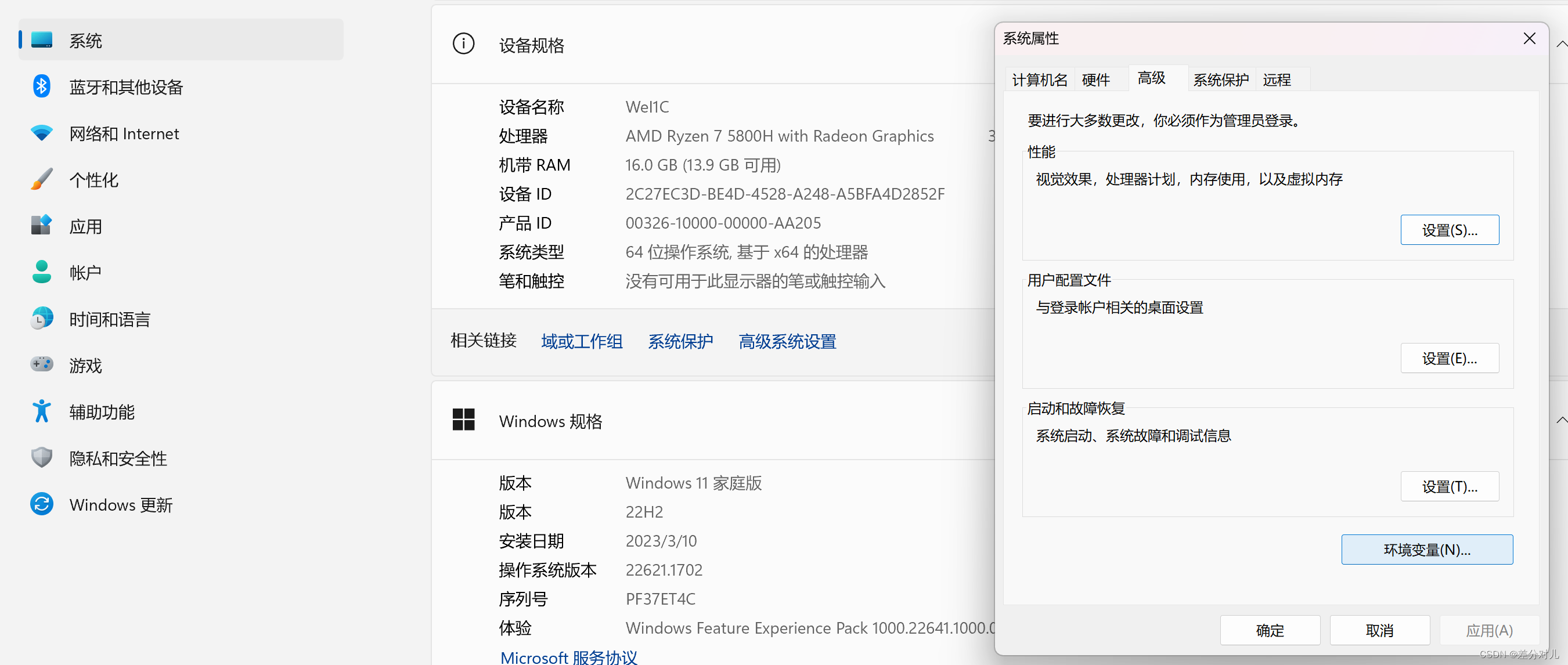
环境变量设置如图所示
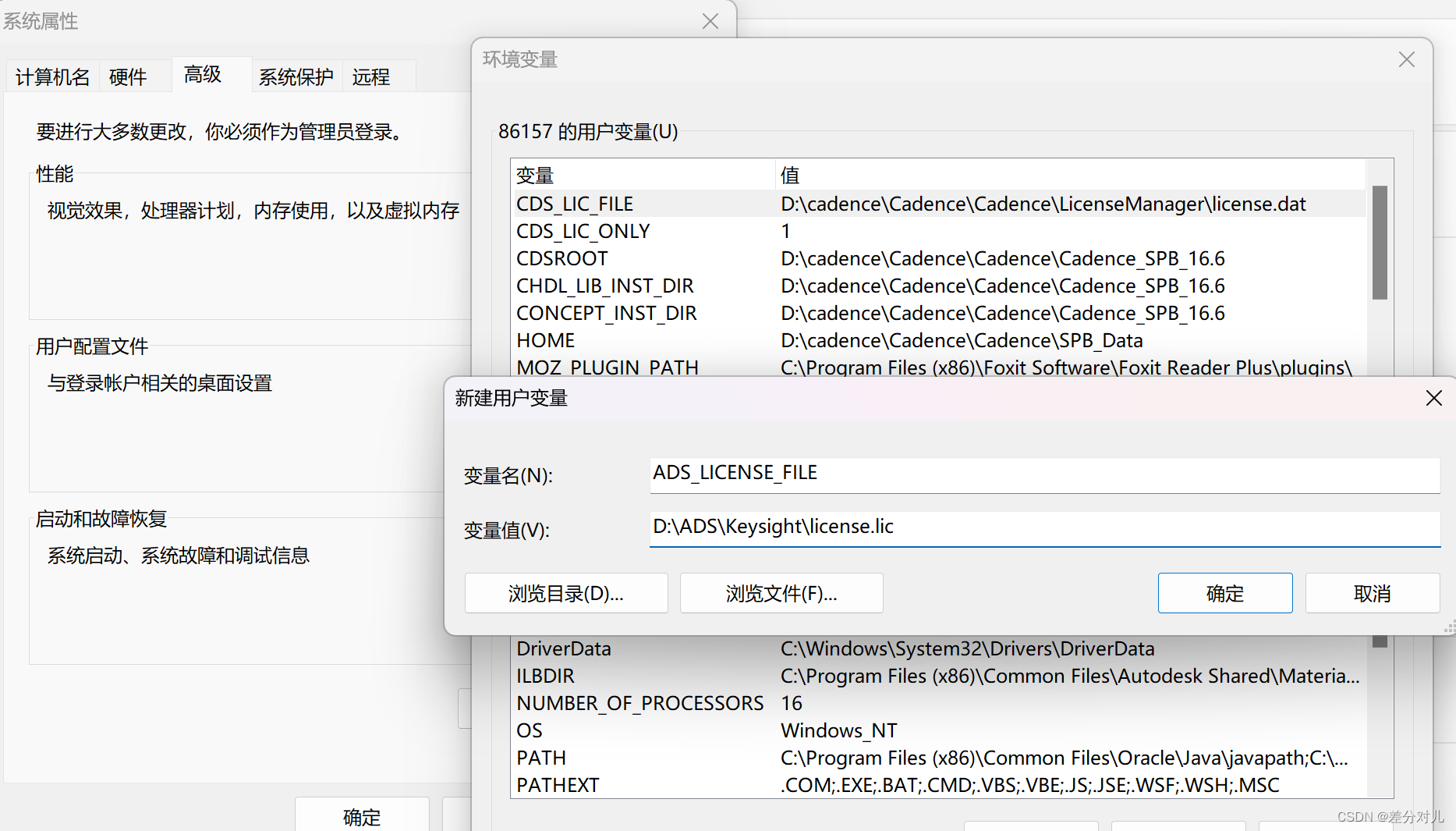
6.双击下图的下载文件中的注册表
7.到此,咱们的安装就完成了!
2.史密斯圆图仿真
创建一个workspace->创建一个原理图->Tools->Smith Chart
终于出来了史密斯圆图的调试口。
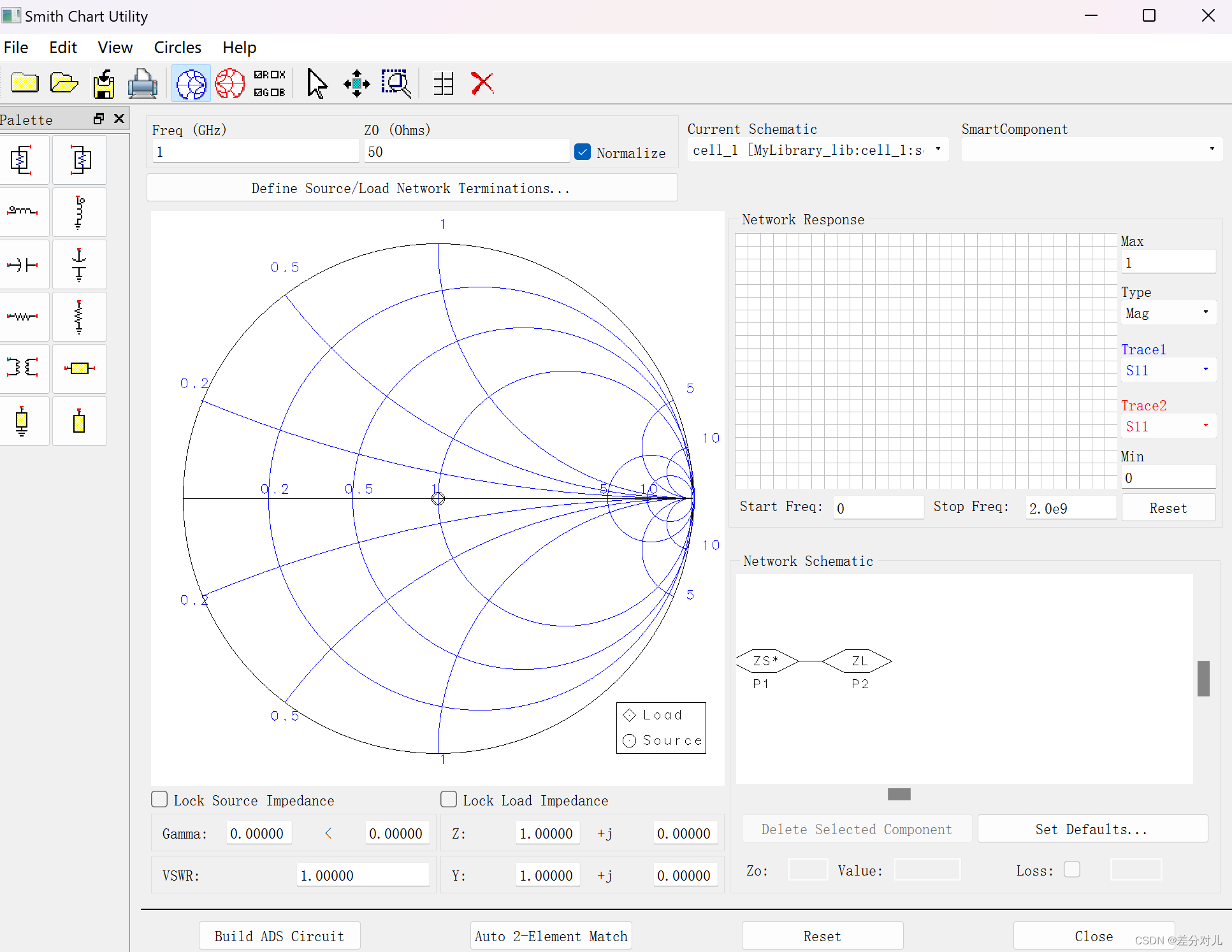
那我们出道题吧😄
首先我们先假设源的值为:0.5-0.3j,负载的值为:2-0.5j,使用史密斯圆图做阻抗匹配。
方法一:分立元器件做阻抗匹配
1.按照功率传输理论,我们把负载的共轭与源做匹配。
图中将源与负载先在图上标出来。
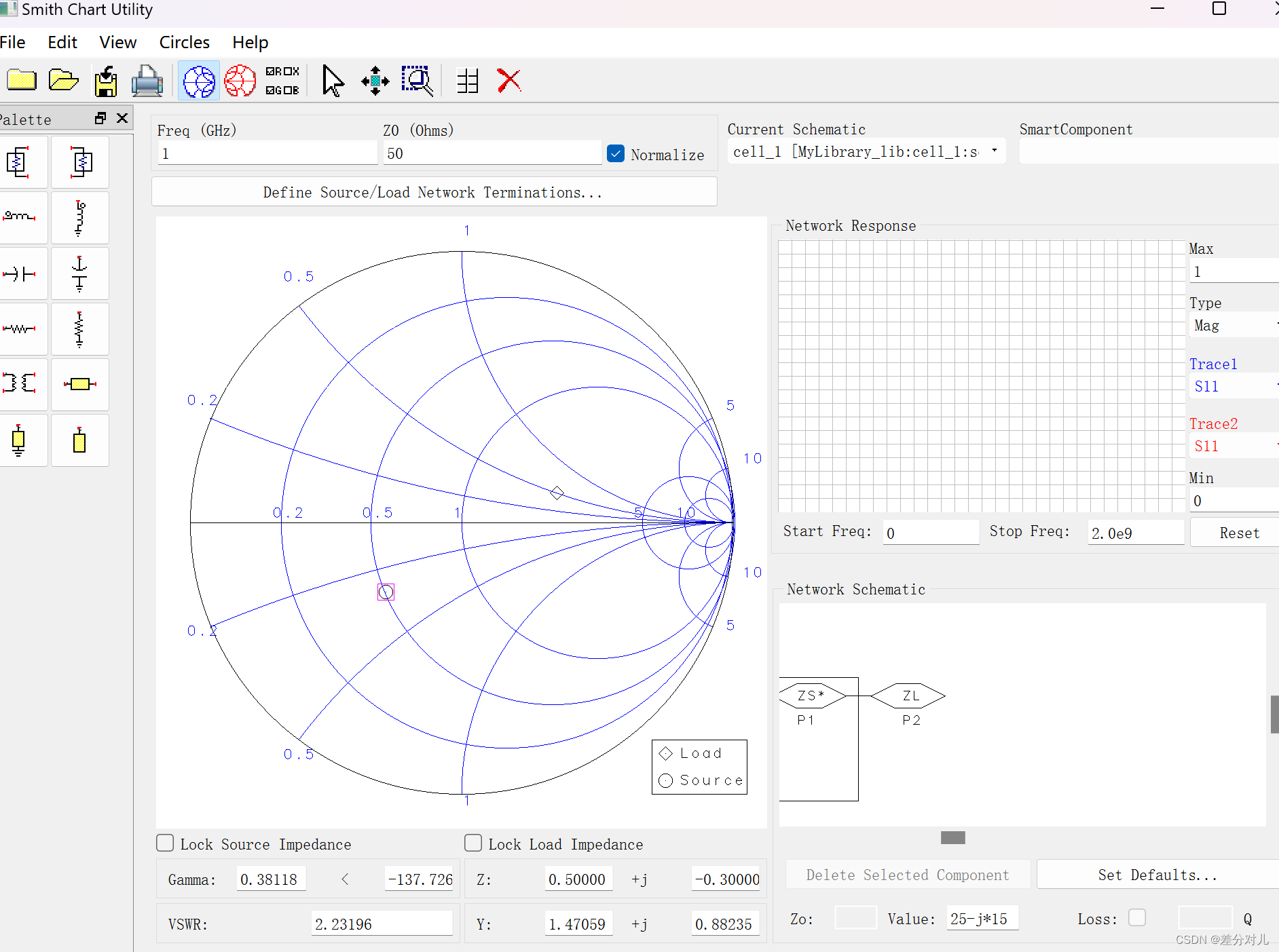
2.将smith chart 的导纳打开,并联一个电容
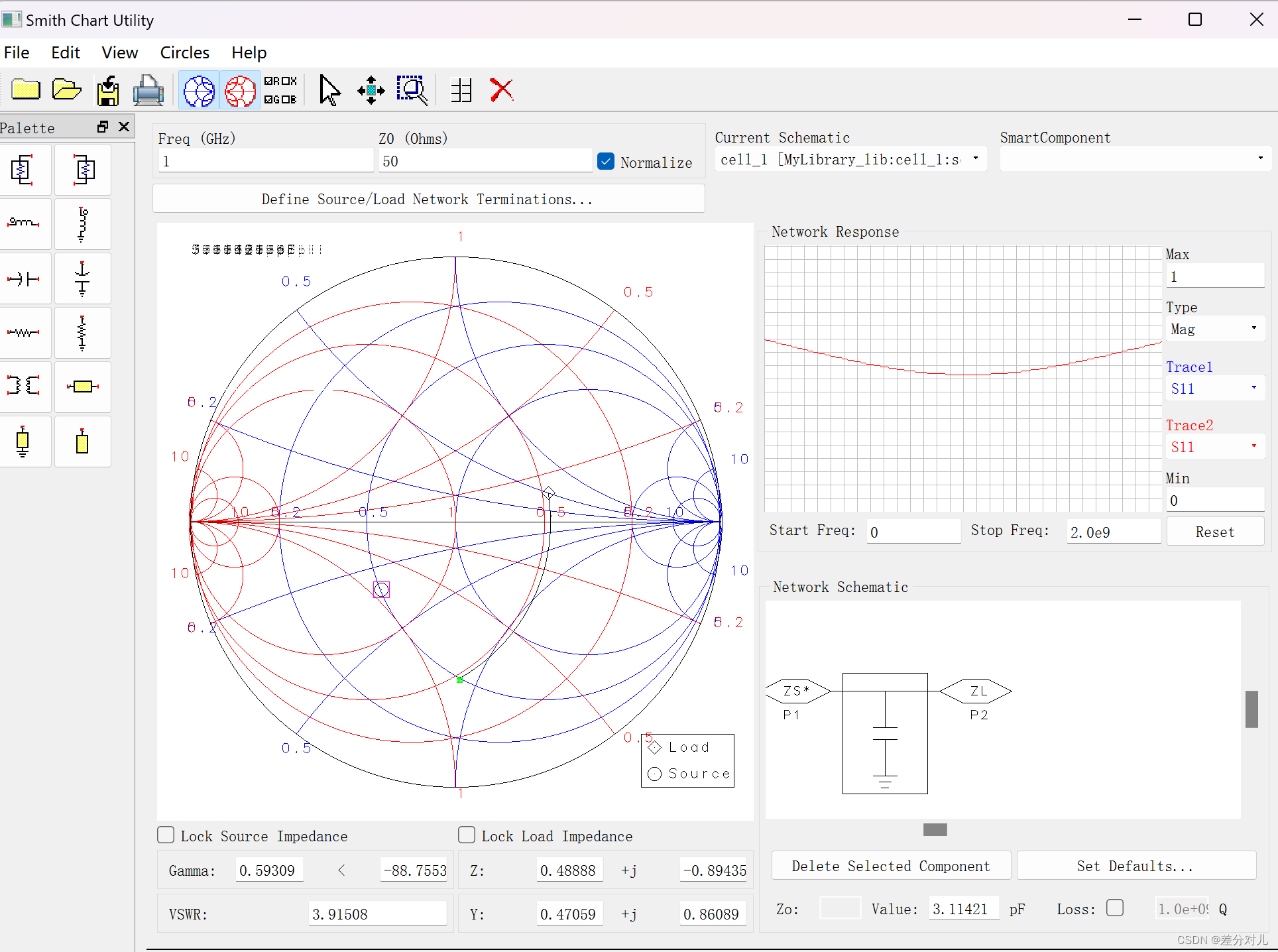
3.将导纳线关掉,再串联一个电感。
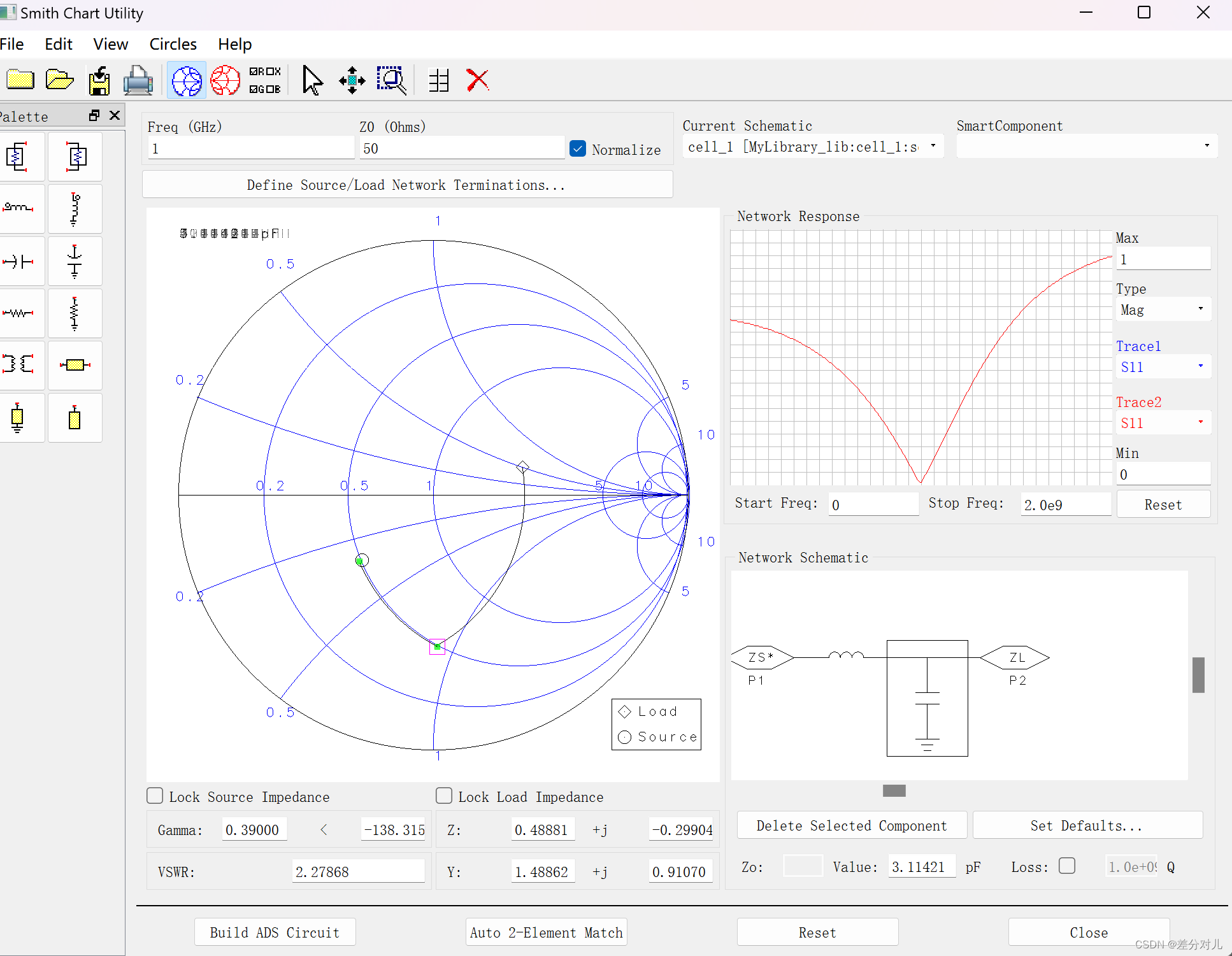
匹配成功,中心点损耗很低。
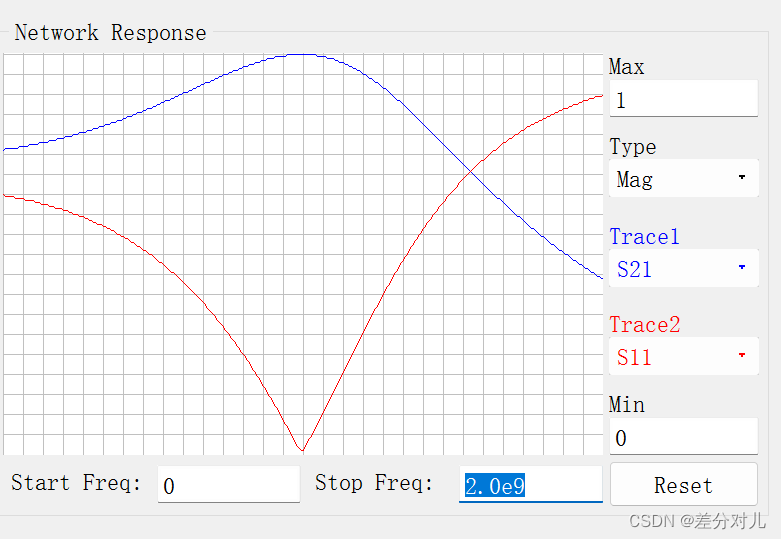
方法二:微带线做阻抗匹配
点击工具栏亮着的微带线图标,连接负载与源端。
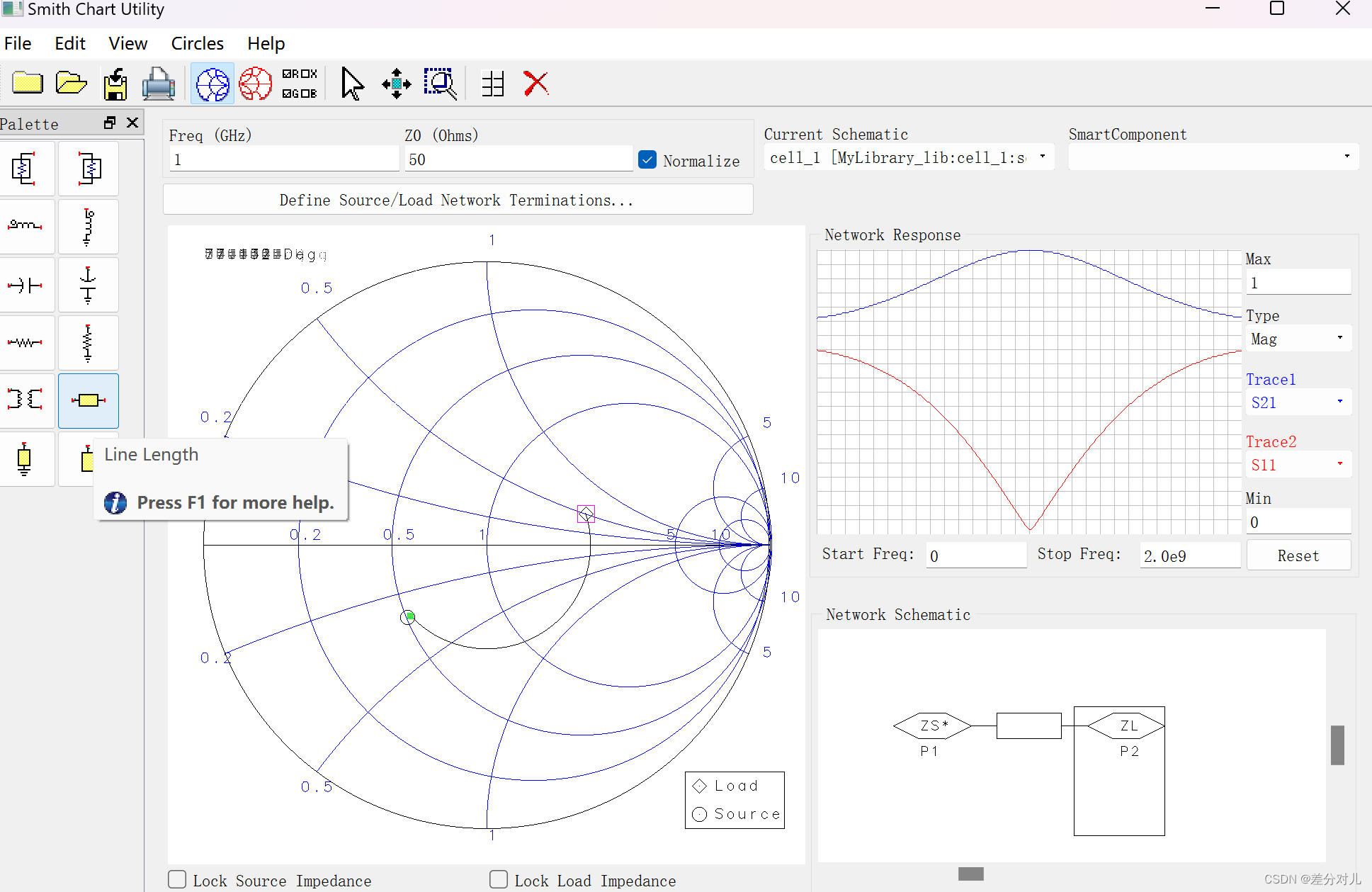
匹配成功,中心点损耗很低。
注:不需要特别记“上感下容,左串右并”口诀等,实际仿真时自然能掌握。
结语
今天就先讲到这,有讲的不对的,评论区欢迎大家指出来。需要安装软件的也可以给我留言,我会及时给大家回复😚😄😁。