本篇文章将详细介绍非牛顿流体函数的具体使用方法。
常见的非牛顿流体有:幂律、CarreauYasuda 模型、交叉模型、Herschel-Bulkley 模型以及粘度曲线等 5 种模型。
表观粘度η
非牛顿流体的粘度μ随剪切速率γ′和剪切应力τ而变化,所以用流动曲线上某一点的τ与γ′的比值来表示在某一值时的粘度,这种粘度称为表观粘度,用η表示:
τ=ηγ′
η=τ/γ′
下面将介绍各模型的参数的含义:
① 幂律(Ostwald-De Wale幂律):
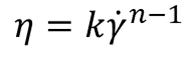
幂律模型适用于广泛剪切变形速率下的假塑性流体或胀塑性流体。
由于其在公式上的简单性,在工程上有较大的实用价值。但是由于它是一个纯粹的经验方程,所以物理意义不够明确。
另外,对于切变率很大或很小的情形,幂指数定律都不适用。
一致性指数:k,也称稠度系数。k值是粘度的度量,但不等于粘度值,而粘度越高,K值也越高;
幂律指数:n,为流动行为指数或非牛顿指数,是与温度有关的参数,n偏离1的程度越大,表明材料非牛顿性越强。;
当n>1时,幂律方程反映剪切变稠的胀塑性流体(如淀粉、蔗糖溶液、涂料等);
当n<1时,幂律方程反映剪切变稀的假塑性流体(如大多数聚合物,番茄酱等);
当n=1时,幂律方程反映牛顿流体k=η0;
最小粘度:流体在幂律模型下适用的最小粘度,n>1时必须要输入;
最大粘度:流体在幂律模型下适用的最小粘度,n<1时必须要输入。
多数高分子流体是假塑性流体,可以用幂律方程描述,其流动行为指数n=0.15~0.6。
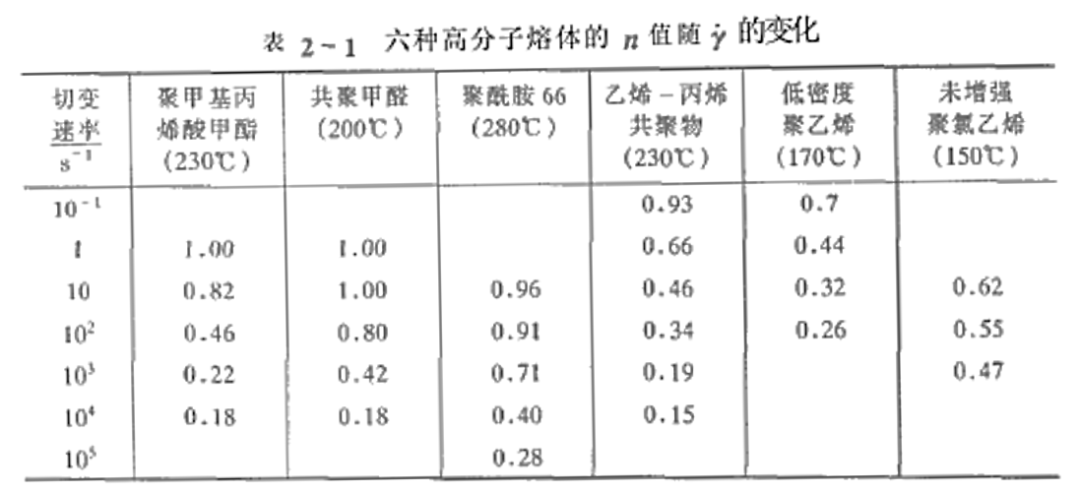
② Carreau Yasuda模型:
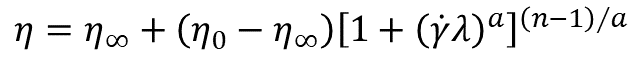
Carreau Yasuda方程既反映高剪切速率下的假塑性,又反映低剪切速率下的牛顿性。能够描写比幂律方程范围更广的流动性质。
幂律指数:n,为流动行为指数或非牛顿指数,一般n<1;
时间常数:λ,也称松弛时间,指材料受力变形,外力解除后恢复正常状态所需的时间;
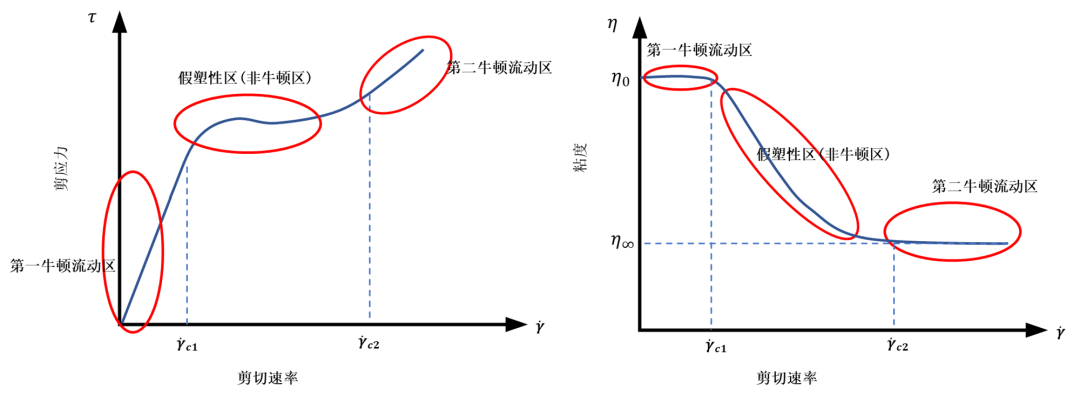
零剪切粘度:η_0,也称第一牛顿粘度。剪切速率很小时,聚合物粘度较大,且通常为一个定值,所以常作为聚合物粘度的标准;
无限剪切粘度:η_∞,也称第二牛顿粘度。剪切速率非常大时,聚合物大分子链容易发生降解,有时可取为0;
Yasuda指数:a,控制从第一牛顿流动区到剪切变稀指数区域的粘度转变速度的常数(a<1时,转变区域扩大),当a取2时就是 Carreau模型。
例如:下图是3%乳清蛋白分离物和0.4%黄原胶假塑性溶液的粘度曲线。
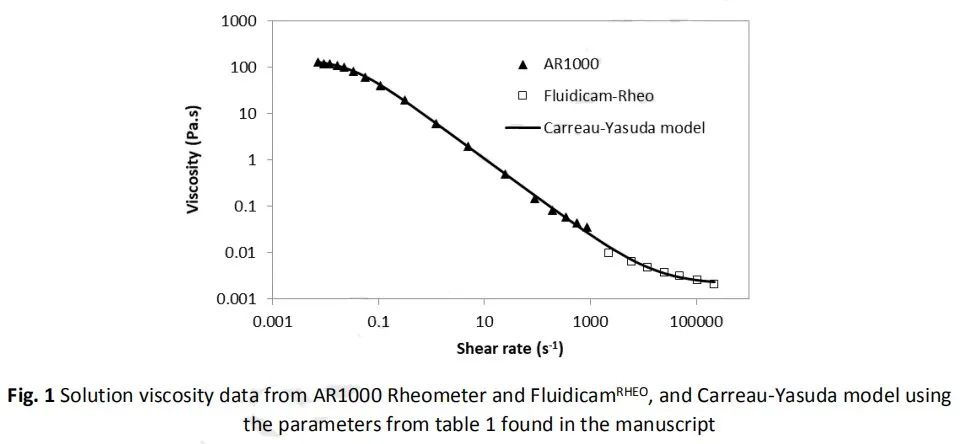
如果应用Carreau-Yasuda流变方程进行拟合,拟合参数如下:
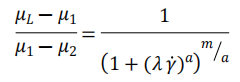

Carreau Yasuda模型适用于高分子聚合物的剪切变稀行为,而且是最常用于表征人体血液粘稠度的非牛顿模型之一。
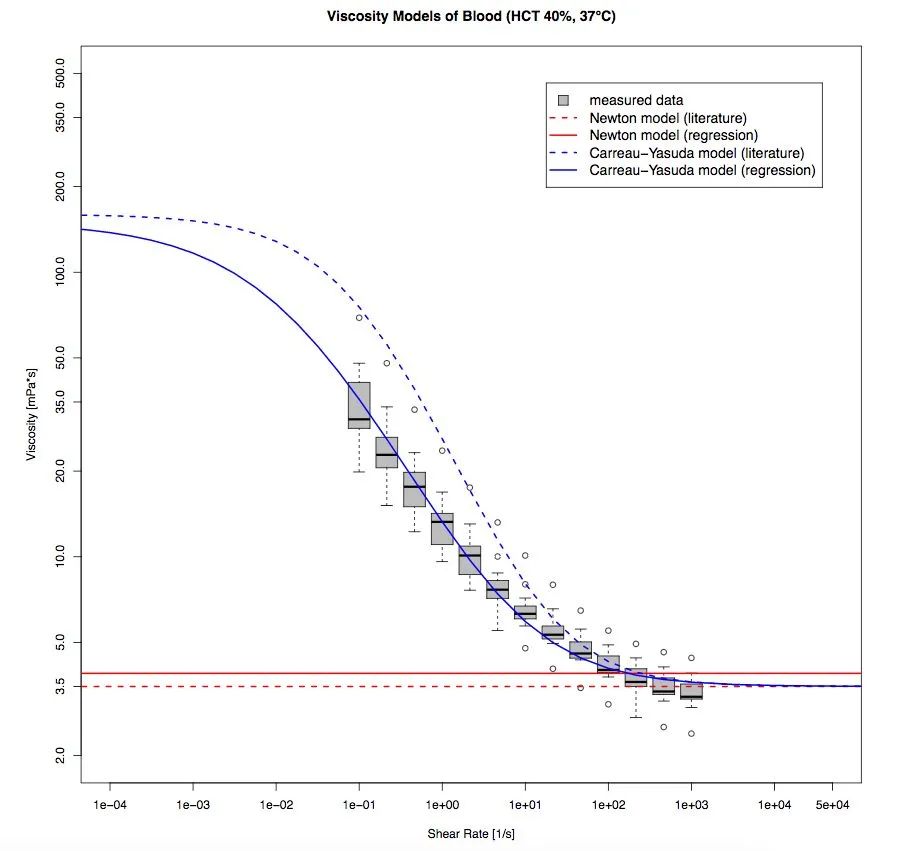
不同模型血液粘度值测量数据的对比
(图片摘自 G. Mach 等人员在 COMSOL 用户年会 2016 慕尼黑站发表的演示作品)
③ 交叉模型:
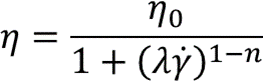
交叉(Cross)模型可全面描述“S”形流动曲线反应的转折,石油化工领域应用较多,通常用来描述沥青等热塑性材料。
幂律指数:n,为流动行为指数或非牛顿指数,n可取大于1或小于1的数值;
时间常数:λ,也称松弛时间,指材料受力变形,外力解除后恢复正常状态所需的时间;
零剪切粘度:η_0,也称第一牛顿粘度。剪切速率很小时,聚合物粘度较大,且通常为一个定值,所以常作为聚合物粘度的标准;
交叉(Cross)模型还有一些其他表达形式,例如:Cross-Exp模型、Cross-WLF模型。
Cross-Exp模型:
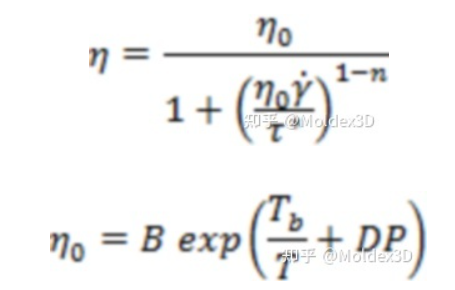
Cross-WLF模型 :
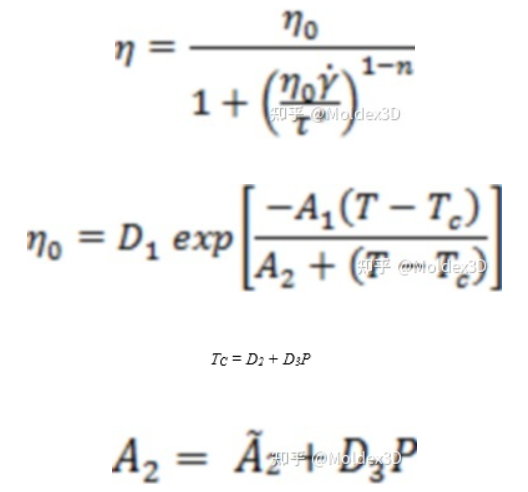
④ Herschel-Bulkley模型:
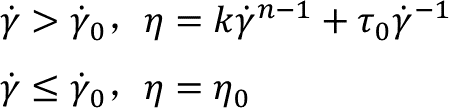
Herschel-Bulkley模型可以描述带有屈服应力的剪切变稀或剪切增稠流体。
模型中的流动行为指数n=1的情况下,Herschel-Bulkey模型将退化为Bingham模型,可用来描述宾汉流体。
一致性指数:k,也称稠度系数。k值是粘度的度量,但不等于粘度值,而粘度越高,K值也越高;
幂律指数:n,为流动行为指数或非牛顿指数,是与温度有关的参数,n偏离1的程度越大,表明材料非牛顿性越强;
当n>1时,为广义宾汉流体剪切变稠;
当n<1时,为广义宾汉流体剪切变稀;
当n=1时,为理想宾汉流体;
屈服应力:τ_0,只有当外力超过该应力才发生流动;
临界剪切速率:γ′_0,屈服剪切速率,开始流动时的剪切速率。
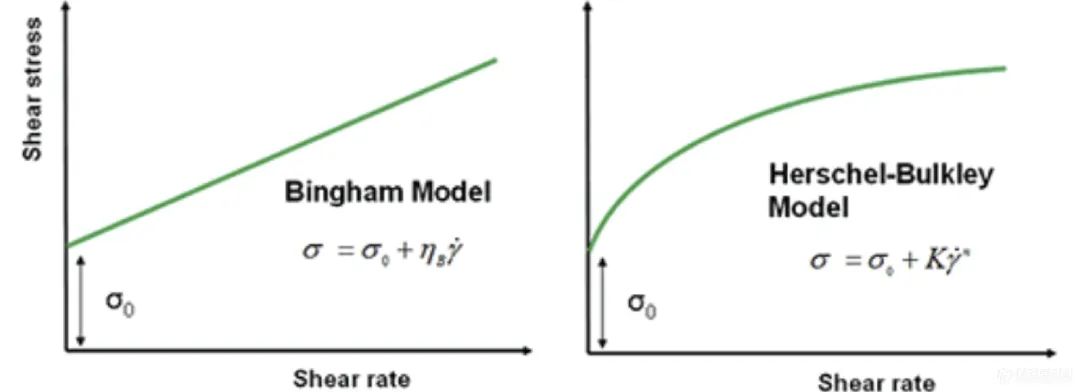
线性坐标下的典型的Bingham与Herschel-Bulkley模型拟合
⑤ 粘度曲线:输入粘度与剪切速率的离散数据点。
非牛顿流体模型很多,如果遇到软件没有提供的模型,可以在Excel表格里编辑好后,通过粘度曲线进行定义。

一些常见的流动模型
本来想这次给大家分享下案例,奈何篇幅太长,下次一定 。
。


口说无凭,要不先预热一下吧
水滴自由下落

非牛顿流体自由下落
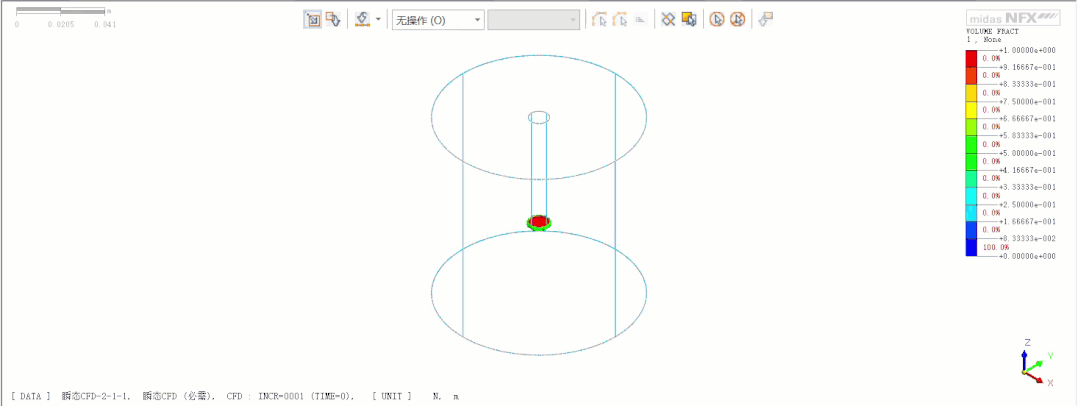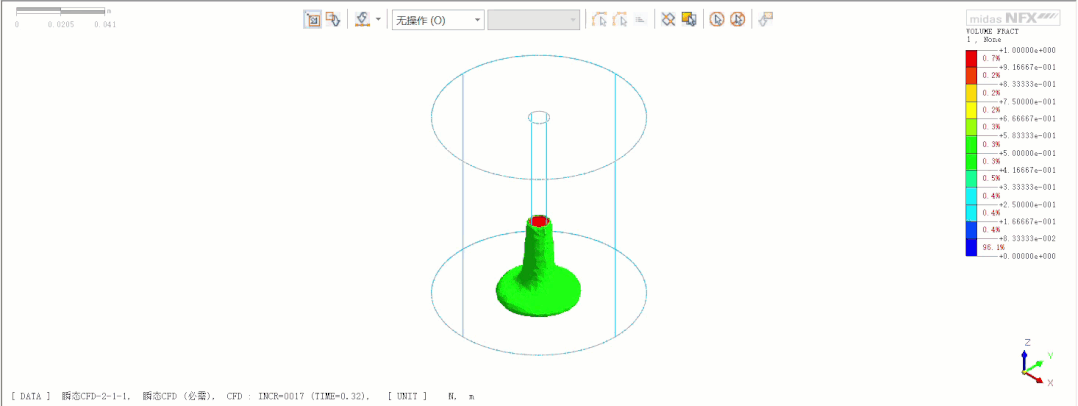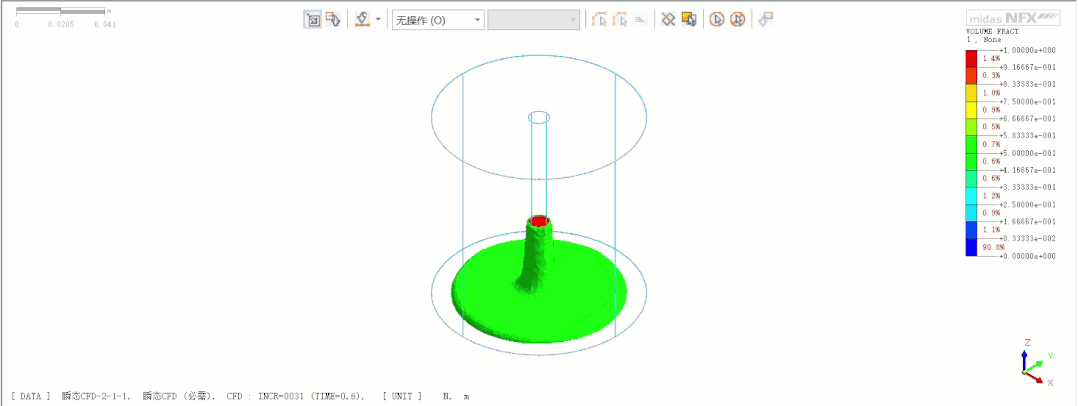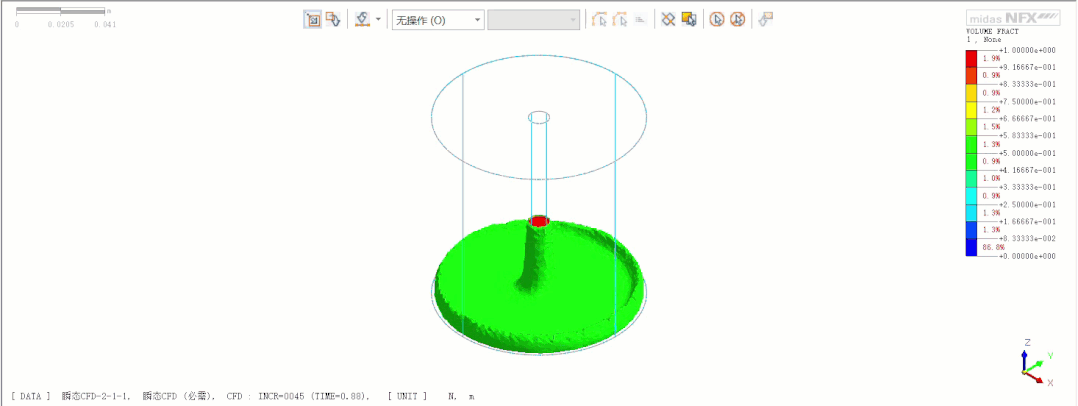
非牛顿流体注液过程
参考资料:
[1] J. Sepulveda, A. Montillet, D. Della Valle, C. Loisel, A. Riaublanc, Deformation of gas-liquid interfaces in a non-Newtonian fluid at high throughputs inside a microfluidic device and effect of an expansion on bubble breakup mechanisms, Chemical Engineering Science (2019).
[2] White Paper – Understanding Yield Stress Measurements.
[3] Moldex3D模流分析知识点大百科-材料性质与模型(1/4) - 知乎 (zhihu.com)
[4] A13C2A29F91287E8DEC1A117259_269C7DBF_C13EB.pdf (hzau.edu.cn)



