【Hardware】【史密斯圆图】

史密斯圆图是什么：

该图表由菲利普·史密斯于1939年发明，史密斯曾说过，“在我能够使用计算尺的时候，我对以图表方式来表达数学上的关联很有兴趣”
Alt
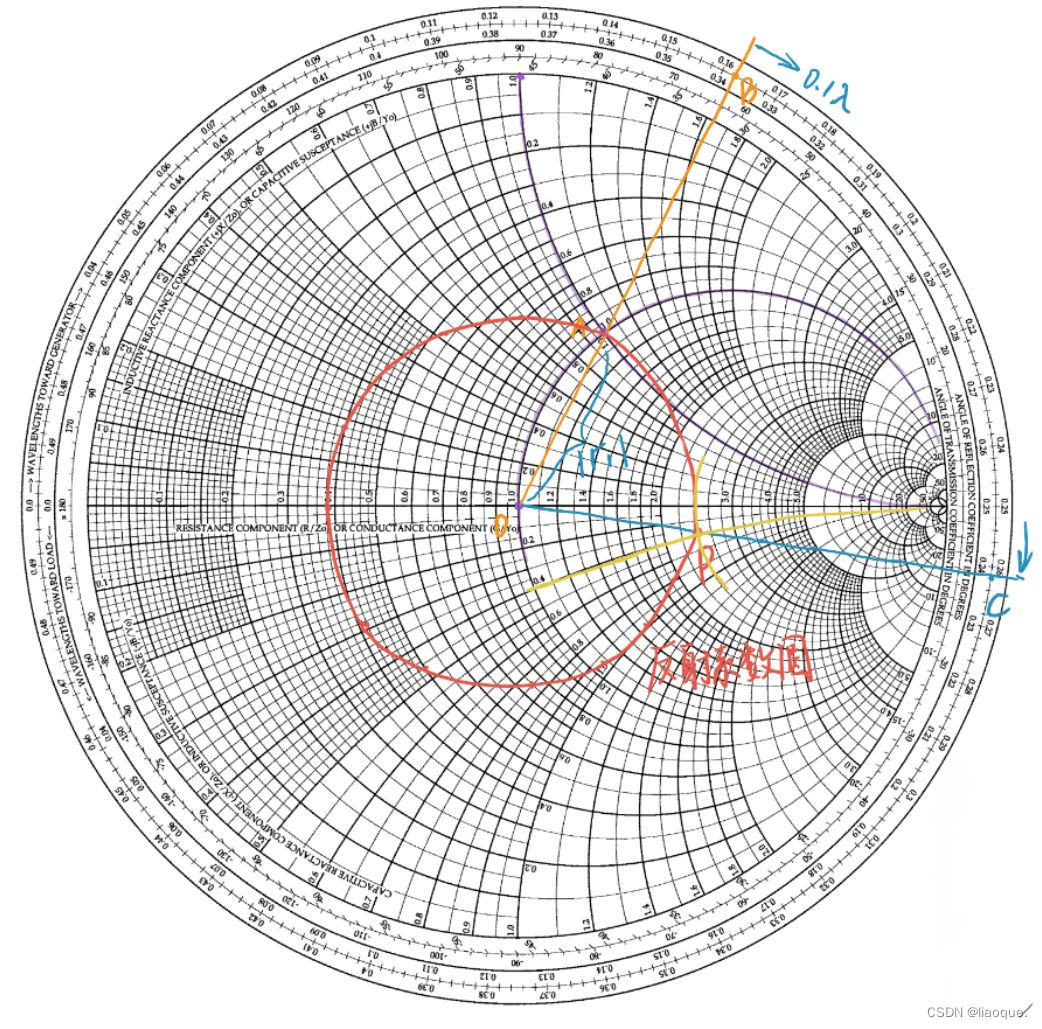
其中 T 代表反射系数（reflection coefficient）。
Zl是归一阻抗值，即 ZL/Z0。ZL为传输线路的阻抗值，Z0为传输线的特征阻抗，通常为50ohm。

史密斯圆图如何产生：

也许是受到黎曼几何的启发，将一个平面坐标系掰弯成一个圆形坐标系。用一个圆形表示一个无穷大的平面。

什么是无穷大平面：

首先复习下电阻、电容、电感的概念。

在电路中对电流起阻碍作用的叫阻抗，用Z表示，是一个复数，实部为电阻，虚部为电抗。
电容在电路中对交流电所起的阻碍作用称之为容抗，电感在电路中对交流作用所起的阻碍作用称之为感抗，二者合称为电抗。

电阻：R
容抗：Z = 1/jwC
感抗：Z = jwL
Z = R + i(wL - 1/wC)，即电阻+感抗+容抗；
1）如果 wL - 1/wC > 0，则称之为感性负载；
2）如果 wL - 1/wC < 0，则称之为容性负载；

我们知道，电路中阻抗不仅能改变电压的幅值，也能改变电压的相位。
如此，我们在一个复平面内，X轴为实部，Y轴为虚部，可以表示任意一个阻抗值。

举例如下：RLC串联电路中，交流电压 U=220V，频率 f=50Hz，R=30R， L=445mH，C=32mF。
1）XL = 2πfL = 140R，XC = 1/2πfC = 100R；
|Z| = (R^2 + (XL - XC)^2 )^0.5 = 50R
I = U/|Z| = 4.4A
2）UR = RI = 132V， UL = XLI = 616V， UC = XCI = 440V；
3）θ = arctan((XL - XC)/R) = arctan(40/30) = 53.1°；
即，总电压超前总电流 53.1° ，电路呈现感性。

Alt
任意一个阻抗的计算结果，我们都可以放在这个复平面内，而各种的阻抗情况，组成了一个无穷大的平面。

反射公式：

信号沿传输线向前传播，每时每刻都会感受到一个瞬态阻抗。如果这个瞬态阻抗是恒定的，那么它会继续向前传播；如果这个瞬态阻抗发生变化，无论是什么引起的，无论如何变化，信号都会发生发射。

衡量反射的重要指标为：反射系数，用于表示反射电压和原传输信号电压的比值：
Alt
Z0为传输线特征阻抗（我们假定为恒定的50欧姆），Zin为信号遇到的瞬时阻抗，假设其为100欧姆，则：

T = （100 - 50）/（100 + 50）= 1/3，即信号约有三分之一被反射。

如果传输信号电压为 3.3V，则有 1.1V的电压被反射。

纯电阻性负载是我们研究反射的基础，阻性负载主要分为四种情况：
1）阻抗增加；2）阻抗减小；3）开路；4）短路（阻抗突然变为0）。

《信号完整性》书中有对反射过程的完整介绍，截一图如下：
Alt
初始电压，即源端电压Vs（2V）经过Zs（25R）和传输线阻抗（50R）分压，Vinitial = 1.33V
后续反射按照反射系数公式计算如下：
Alt
源端反射：源端阻抗（25R）和传输线阻抗（50R），反射系数为 0.33；
终端反射：终端阻抗（无穷大）和传输线阻抗（50R），反射系数为 1；

按照每次反射的幅度和时延，将波形叠加得到如下波形图，此为阻抗不匹配造成的信号完整性不好的结果：

Alt
Alt
如此，我们就定义 Z0 = 50R，根据反射公式，得到一个重要的结论如下：
Alt
每一个Zin对应一个唯一的反射系数T。接下来，我们把对应关系映射到之前提及的复平面。
Z = ZL/Z0 = (R+jX)/Z0 = r + jx，其中 r = R/Z0，x = X/Z0。
则反射公式对应为：T = Ti + Tj = （ZL - Z0）/（ZL + Z0）=（z-1）/（z+1）=（r+jx-1）/（r+jx+1）。
让我们忘记Zin，只记得z和反射系统T。