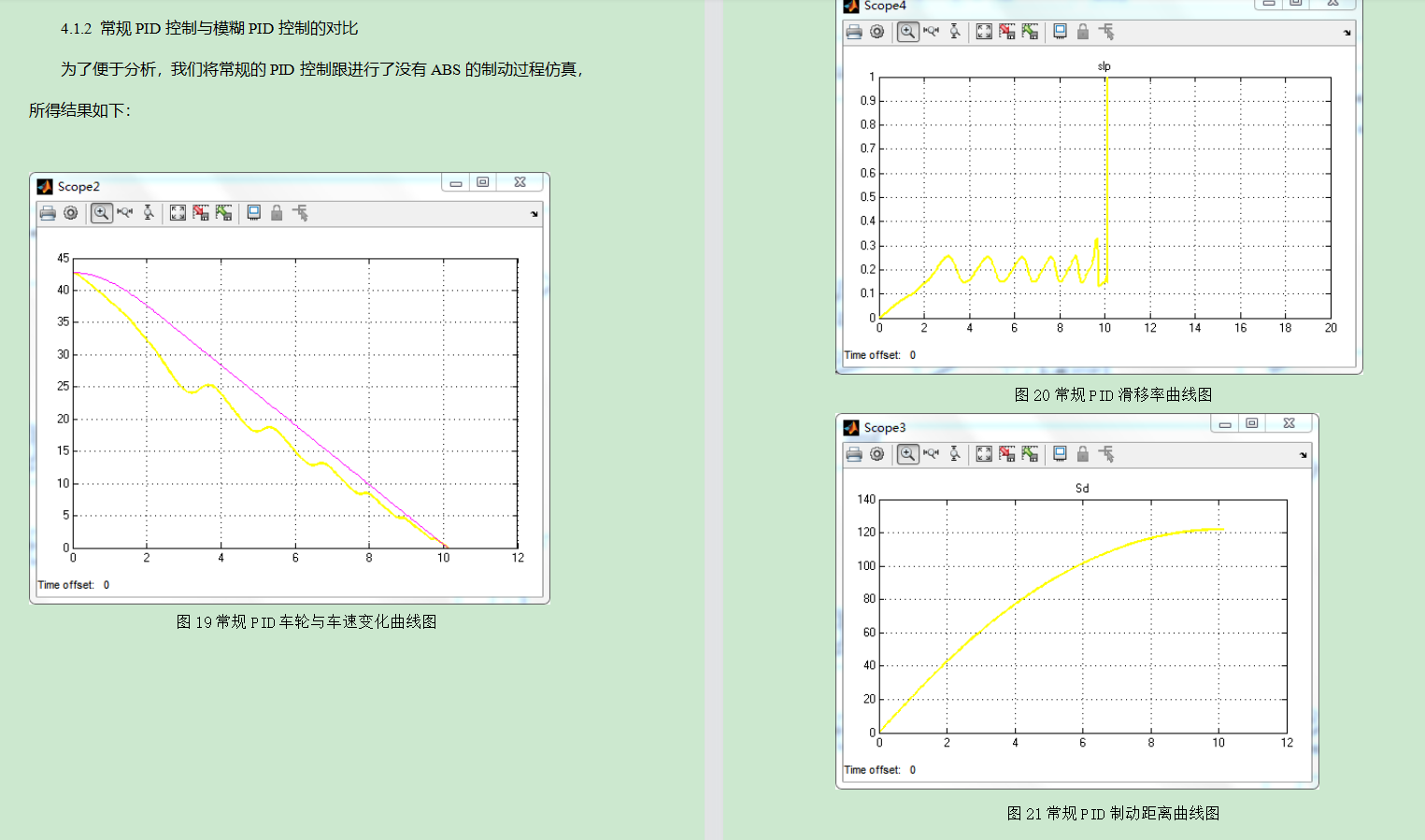
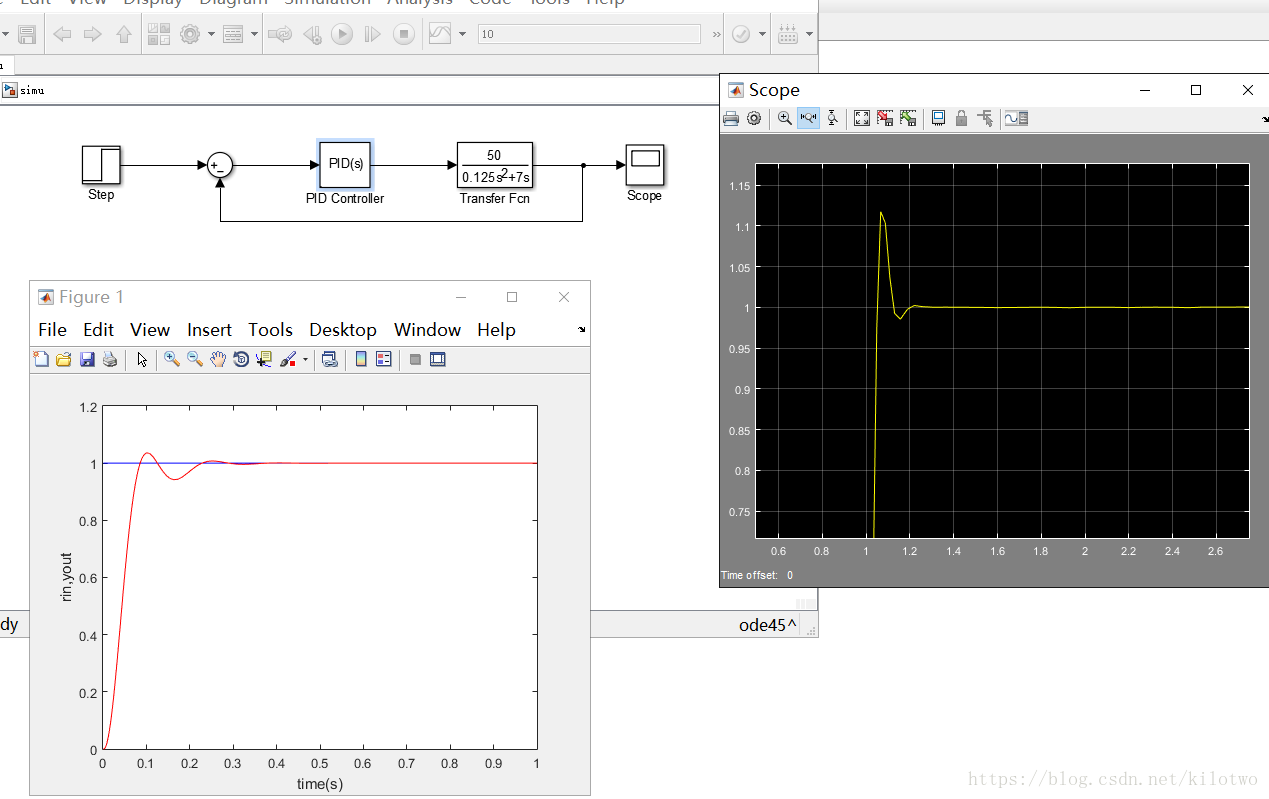
最近在学优化算法,接触到了经典寻优算法之粒子群PSO,然后就想使用PSO算法来调节PID参数,在试验成功之后将此控制算法应用到了空气起动系统上,同时与之前的控制器进行对比看看哪种控制效果最好。
0 引言
PID参数整定主要有两种:① 传统整定方法:幅值-相角裕度法、工程整定法、Z-N频率响应方法等,传统整定方法需要一定的工程经验,且只能获得相对意义上的最佳参数组合。② 新兴智能寻优算法如神经网络法、粒子群优化法等,其能自主的在约束条件的限制下寻找最优的控制参数,智能控制的发展为PID的参数整定提供了新的途径。
粒子群算法(PSO)属于种群搜索的自适应优化算法,其基本思想是把鸟群中的每个鸟看成一个粒子,鸟群寻找食物的过程中,不确定食物的具体位置,没有具体的飞行目标。只知道自己和食物的位置关系,为了尽快找到食物,它们通过对距食物最近的鸟的附近空间的搜索来达到找到食物的目的。
PSO优化算法因其结构简单,寻优效率高、精度高的特性常被广泛应用到参数整定中。
1 PSO算法原理
粒子群算法的整个寻优过程是:先对粒子群中的初始粒子的位置和速度进行初始化设置,然后进行粒子群算法的迭代过程,在迭代过程中,计算出每次迭代过程中粒子的适应度值,根据适应度值,粒子进行速度和位置信息的更新,直至迭代过程结束。在迭代结束后,得到全局最优粒子,控制器的参数组合也到达预设条件下的最优,以此来提高控制器的控制能力。粒子群算法中主要包括粒子、极值、适应度函数几个要素。
① 粒子:算法的每次迭代都是同时对粒子位置和速度进行更新,粒子位置代表的就是所要求的解,速度是每次迭代时位置的调节步长。为了避免算法中粒子盲目搜索,通常要根据实际控制量的具体范围设定位置和步长的上下限 [ − X max , X max ] \left[ -X_{\max}\text{,}X_{\max} \right] [−Xmax,Xmax]、 [ − V max , V max ] \left[ -V_{\max}\text{,}V_{\max} \right] [−Vmax,Vmax]粒子的位置和步长更新方式为:
{ v i d k + 1 = w × v i d k + c 1 × r 1 × ( p i d − x i d k ) + c 2 × r 2 × ( p g d − x i d k ) x i d k + 1 = x i d k + v i d k + 1 \begin{cases} v_{id}^{k+1}=w\times v_{id}^{k}+c_1\times r_1\times \left( p_{id}-x_{id}^{k} \right) +c_2\times r_2\times \left( p_{gd}-x_{id}^{k} \right)\\ x_{id}^{k+1}=x_{id}^{k}+v_{id}^{k+1}\\ \end{cases} {vidk+1=w×vidk+c1×r1×(pid−xidk)+c2×r2×(pgd−xidk)xidk+1=xidk+vidk+1式中, v i d k + 1 v_{id}^{k+1} vidk+1 表示第 i i i 个粒子在第 k + 1 k+1 k+1 次迭代中第 d d d 维上的速度信息, x i d k + 1 x_{id}^{k+1} xidk+1 表示第 i i i 个粒子在第 k + 1 k+1 k+1 次迭代中第 d d d 维上的位置信息, c 1 c_1 c1 和 c 2 c_2 c2 为学习因子, w w w 为惯性权重。
② 极值:算法的每次迭代都需要参考两个极值,即全局最优值 p g d p_{gd} pgd 和粒子个体的历史最优值 p i d p_{id} pid 。通过不断比较、计算种群中每个粒子的适应度值来得到这两个极值。
③ 适应度函数: 粒子群算法中,为了检验所求值的优劣,引入适应度函数,目前为止所有的适应度值函数中考量最为综合、合理的评判指标为 ITEA 方法,即 J = ∫ 0 ∝ t ∣ e ( t ) ∣ d t J=\int_0^{\propto}{t\left| e\left( t \right) \right|dt} J=∫0∝t∣e(t)∣dt
PSO算法粒子迭代示意图为:

2 改进PSO算法
由于惯性权重 w w w对于算法的寻优过程影响很大,现在的研究也大多集中在惯性权重的改进方面,来解决粒子群算法容易陷入局部最优的问题。
惯性权重 w w w 的设计方法有:① 线性递减惯性权重策略: w = w max − ( w max − w min ) t T max w=w_{\max}-\left( w_{\max}-w_{\min} \right) \frac{t}{T_{\max}} w=wmax−(wmax−wmin)Tmaxt② 非线性递减惯性权重策略: w = w max − ( w max − w min ) ( t T max ) 2 w = w max − ( w max − w min ) [ 2 t T max − ( t T max ) 2 ] w=w_{\max}-\left( w_{\max}-w_{\min} \right) \left( \frac{t}{T_{\max}} \right) ^2 \\ w=w_{\max}-\left( w_{\max}-w_{\min} \right) \left[ \frac{2t}{T_{\max}}-\left( \frac{t}{T_{\max}} \right) ^2 \right] w=wmax−(wmax−wmin)(Tmaxt)2w=wmax−(wmax−wmin)[Tmax2t−(Tmaxt)2] 通过对比,在相同的条件下,采用非线性惯性权重的粒子群算法收敛速度更快,陷入局部最优的情况减少,得出的控制器参数更加有效。
3 PSO-PID控制器设计
利用 PSO 算法的寻优特性对 PID 控制器的三个参数进行调整,将 PSO 算法的维度设定为3,每个粒子的位置信息在这 3 个维度的分解量都对应的表示一组 PID 参数值。粒子群PSO-PID优化流程如下图所示。

4 仿真结果与分析
将PSO-PID控制方法与PID控制、RBF-PID控制、ADRC控制这三种控制方法进行对比,在相同的参数下进行仿真,仿真模型以及结果如下。
① 搭建模型

② PSO-PID的迭代过程和ITAE变化曲线为


可以看出,随着迭代次数的增加,群体适应值在不断地减小直至稳定在一个值左右。
③ PID参数变化曲线:

可以看出比例系数 Ki 随着迭代次数的增加逐渐减小,而积分系数 Ki 和微分系数 Kd 始终保持在一个值,无明显变化。
④ 寻优前后的跟踪对比:

可以看出寻优前与寻优后存在明显的改进,寻优后的跟踪曲线控制效果更好,能更好的跟踪上参考曲线。
⑤ 四种控制器的控制效果对比:

可以看出最后的控制效果从好到坏依次为:PID < RBF-PID < PSO-PID < ADRC。但是,ADRC也有它的缺点,即当采样时间不在0.001~0.0001这个区间内时,其控制效果达不到最好。在实际的PLC控制系统中,对于一般优先级的模块来说,PLC的采样时间在100ms或10ms这种量级,达不到1ms甚至0.1ms这种级别,所以当采样时间过大时,可能ADRC的控制效果还不如PID控制。
另外,我还发现个问题,几乎所有文献中,使用PSO-PID控制器的参考输入都是用的阶跃输入信号或者常值输入信号,在我多次使用其他类型输入仿真试验之后得出结论,使用阶跃信号的PSO优化效果最好,调优效果最明显。
5 参考文献
[1] 曹刚,令狐克均,吴怀超,等. 基于PSO-PID的重型AT主油压调节的研究[J]. 机床与液压,2019,47(16):152-156
[2] 康日晖. 基于改进PSO-PID算法的四轴飞行器飞控系统研究[D]. 山西:太原理工大学,2018.
[3] 高杰. 基于粒子群算法的微电网经济调度优化[D]. 长江大学,2021.
[4] 杜文正,谢政,童国林. 桥式起重机PSO-PID防摆控制器的设计[J]. 机床与液压,2013,41(13):98-100.