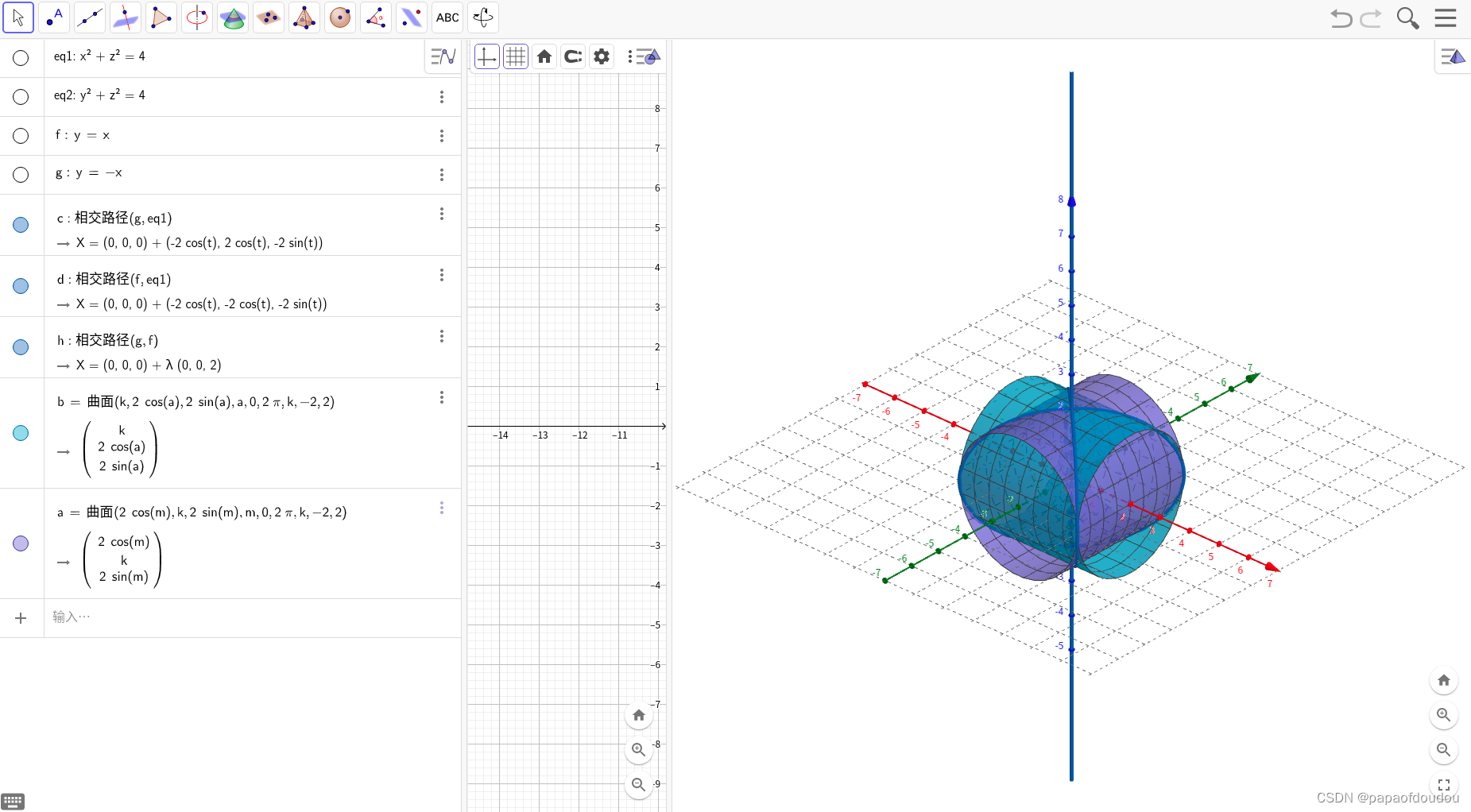
曲线——曲率
- 二维参考链接
- 三维参考连接
- 用到的补充知识:
- 点乘 叉乘
- 空间曲线的切线
二维参考链接
离散点曲率计算-三种方法
MATLAB 求取离散点的曲率最大值
⭐求离散点的曲率(非等间隔)
精品:Spline导数及曲率计算(判断曲线的弯曲程度)
已知曲线函数表达式的曲线曲率计算
高等数学入门——曲率的定义及其公式推导
⭐ 参数方程形式的曲率公式及推导
三维参考连接
空间曲线的切线和法平面求法
⭐1⭐空间曲线的曲率计算方法
⭐2⭐求曲线的曲率计算公式 注意 :这个里面的回答第二条应该是 k=|r’×r"|/(|r’|)^3 因为|r’|是向量的模,本身里面就有根号了。
? 以上两个星星链接(2按改的黄色公式)得到的参数方程的曲率计算公式,化简后,结果一样。
%参数方程表示的三维曲线计算公式,
% r =[x(t),y(t),z(t)] 参数方程表达式 =》 可看作质点在空间中的运动轨迹
% r' =[x1(t),y1(t),z1(t)] 一阶导 =》 质点的速度向量
% r''=[x2(t),y2(t),z2(t)] 二阶导 =》 质点的加速度向量
syms r1 r2 x1 y1 z1 x2 y2 z2;
%★1★化简公式
r1 = sqrt((x2^2+y2^2+z2^2)*(x1^2+y1^2+z1^2)-(x1*x2+y1*y2+z1*z2)^2)/((sqrt(x1^2+y1^2+z1^2))^3);
%★2★公式带入
r2 = sqrt((y1*z2-z1*y2)^2+(z1*x2-x1*z2)^2+(x1*y2-x2*y1)^2)/((sqrt(x1^2+y1^2+z1^2))^3);
% 我使用simpify函数也没化简出来。。。
% 简单点:随便给几个值,即假设在t0处的一阶二阶导数值已知,带入看看上面两个公式计算结果是不是一样
x1 = 6; y1 = 3; z1 = 5;
x2 = 3; y2 = 4; z2 = 2;
% 得到结果一样哒,说明这俩公式化简是一样的,这种计算曲率公式是对的
ans1 = double(subs(r1))
ans2 = double(subs(r2))
用到的补充知识:
点乘 叉乘
-
二维意义:
|向量c|=|向量a×向量b|=|a||b|sin<a,b>
向量c的方向与a,b所在的平面垂直,且方向要用“右手法则”判断(用右手的四指先表示向量a的方向,然后手指朝着手心的方向摆动到向量b的方向,大拇指所指的方向就是向量c的方向)。
- 三维: 向量点乘(内积)和叉乘(外积、向量积)概念及几何意义解读