主曲率，主方向，高斯曲率与平均曲率公式与matlab代码

- 先上结论
- Weingarten变换
- 最后是代码啦

先上结论

在这里插入图片描述

Weingarten变换

在这里插入图片描述

最后是代码啦

在离散情况下，数据表示为X,Y,Z（X，Y由meshgrid产生，Z是曲面的值）像这样：
在这里插入图片描述
那么r=r(u,v)是什么呢？
当然就是r=[x,y,z]=[x(row,col),y(row,col),z(row,col)]啦，即u，v就是网格1,2,3…
所以有：
[Xu,Xv] = gradient(X);
[Yu,Yv] = gradient(Y);
[Zu,Zv] = gradient(Z);
等等这样的代码啦。
matalb 代码如下：

function   [K,H,Pmax,Pmin,D1,D2] = surfcurvature(X,Y,Z)
% K AND H ARE THE GAUSSIAN AND MEAN CURVATURES, RESPECTIVELY.
% Pmax AND Pmin ARE THE MINIMUM AND MAXIMUM CURVATURES AT EACH POINT, RESPECTIVELY.
% d1,d2 ARE THE MAIN DIRECTIONS% First Derivatives
[Xu,Xv] = gradient(X);
[Yu,Yv] = gradient(Y);
[Zu,Zv] = gradient(Z);% Second Derivatives
[Xuu,Xuv] = gradient(Xu);
[Yuu,Yuv] = gradient(Yu);
[Zuu,Zuv] = gradient(Zu);[Xuv,Xvv] = gradient(Xv);
[Yuv,Yvv] = gradient(Yv);
[Zuv,Zvv] = gradient(Zv);% Reshape 2D Arrays into Vectors
Xu = Xu(:);   Yu = Yu(:);   Zu = Zu(:); 
Xv = Xv(:);   Yv = Yv(:);   Zv = Zv(:); 
Xuu = Xuu(:); Yuu = Yuu(:); Zuu = Zuu(:); 
Xuv = Xuv(:); Yuv = Yuv(:); Zuv = Zuv(:); 
Xvv = Xvv(:); Yvv = Yvv(:); Zvv = Zvv(:); Xu          =   [Xu Yu Zu];
Xv          =   [Xv Yv Zv];
Xuu         =   [Xuu Yuu Zuu];
Xuv         =   [Xuv Yuv Zuv];
Xvv         =   [Xvv Yvv Zvv];% First fundamental Coeffecients of the surface (E,F,G)
E           =   dot(Xu,Xu,2);
F           =   dot(Xu,Xv,2);
G           =   dot(Xv,Xv,2);m           =   cross(Xu,Xv,2);
p           =   sqrt(dot(m,m,2));
n           =   m./[p p p]; [s,t] = size(Z);% [nu,nv] = gradient(reshape(n,s,t,3));
% Nu = reshape(nu,[],3);
% Nv = reshape(nv,[],3);% Second fundamental Coeffecients of the surface (L,M,N)
L           =   dot(Xuu,n,2);
M           =   dot(Xuv,n,2);
N           =   dot(Xvv,n,2);% Gaussian Curvature
K = (L.*N - M.^2)./(E.*G - F.^2);
K = reshape(K,s,t);% Mean Curvature
H = (E.*N + G.*L - 2.*F.*M)./(2*(E.*G - F.^2));
H = reshape(H,s,t);% Principal Curvatures
Pmax = H + sqrt(H.^2 - K);
Pmin = H - sqrt(H.^2 - K);% a = (L.*G - M.*F)./(E.*G -F.*F);
% b = (M.*E - L.*F)./(E.*G -F.*F);
% c = (M.*G - N.*F)./(E.*G -F.*F);
% d = (N.*E - M.*F)./(E.*G -F.*F);
% W = permute(reshape([a b c d]',2,2,[]),[2,1,3]);%MAIN DIRECTIONS
D1=(Pmax(:).*G-N).*Xu+(M-Pmax(:).*F).*Xv;
D2=(Pmin(:).*G-N).*Xu+(M-Pmin(:).*F).*Xv;
nd1 = sqrt(dot(D1,D1,2));
nd2 = sqrt(dot(D2,D2,2));
D1=D1./[nd1 nd1 nd1];
D2=D2./[nd2 nd2 nd2];D1=reshape(D1,s,t,3);%k1's MAIN DIRECTION
D2=reshape(D2,s,t,3);% %RETURN
% curvature.k = K;
% curvature.h = H;
% curvature.pmax = Pmax;
% curvature.pmin = Pmin;
% curvature.d1 = D1;
% curvature.d2 = D2;

有人问调用方法，我举个例子：
假设有曲面z = x^2 + y^2
在此之前补充另一个方法
对于曲面S = S(x,y)，平均曲率H也可以通过下式计算：
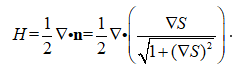
在这里插入图片描述
其中n是S的单位法向量。

% 例子
% 产生函数
clear
close all
clc
f=@(x,y)x.^2+ y.^2;
[x ,y]=meshgrid(linspace(-1,1,100),linspace(-1,1,100));
z=f(x,y);% 解析方法
syms X Y
Nf=gradient(f(X,Y));
Nfx=Nf(1);
Nfy=Nf(2);
H=simplify((diff(Nfx./(1+Nfx.^2+Nfy.^2).^0.5,'X')+diff(Nfy./(1+Nfx.^2+Nfy.^2).^0.5,'Y'))/2);
H=matlabFunction(H);
h=H(x,y);% 数值方法1
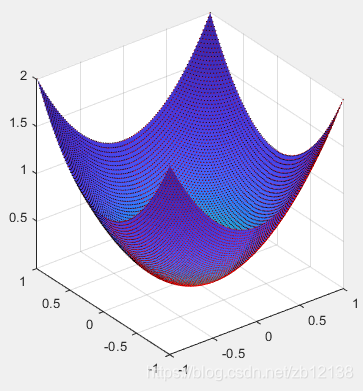
[k,h1,P1,P2,D1,D2] = surfcurvature(x,y,z); %就这么调用surf(x,y,z,h,'LineStyle','none','FaceAlpha',1);
hold on
quiver3(x,y,z,D1(:,:,1),D1(:,:,2),D1(:,:,3),0.2,'r');%极大方向
quiver3(x,y,z,D2(:,:,1),D2(:,:,2),D2(:,:,3),0.2,'k');%极小方向
axis equal% 数值方法2
[NX,NY,NZ]=surfnorm(x,y,z);
% quiver3(x,y,z,NX,NY,NZ);%可视化，用于验证是否是法向量
div=divergence(x,y,-NX,-NY)/2;%注意 此处的-号
h2 = div;%计算误差
fprintf("h - h1 error : %f\n",sum(sum((h-h1).^2)))
fprintf("h - h2 error : %f\n",sum(sum((h-h2).^2)))
%通过有边界误差，去除边界重新计算
mask = true(size(h)); 
mask(1:2,:) = 0; mask(end-1:end,:) = 0;
mask(:,1:2) = 0; mask(:,end-1:end) = 0; 
hh = reshape(h(mask),size(h,1)-4,size(h,2)-4);
h11 =  reshape(h1(mask),size(h,1)-4,size(h,2)-4);
h22 =  reshape(h2(mask),size(h,1)-4,size(h,2)-4);
fprintf("hh - h11 error : %f\n",sum(sum((hh-h11).^2)))
fprintf("hh - h22 error : %f\n",sum(sum((hh-h22).^2)))
%这说明尽管方法1边界误差大，但去除边界后表现好于方法2