本篇参考于:中国大学慕课科学计算与MATLAB统计,专题四“4.5三维曲面”
绘制格网meshgrid
格网和曲面surf&mesh
其他形式surfc,surfl&meshc,meshz
标准三维曲面函数sphere&cylinder
三个方程两个变量使用fsurf和fmesh
1.meshgrid函数生成网格
eg.绘制空间曲线
x=2:6
y=(3:8)'
[X,Y]=meshgrid(x,y)
Z=randn(size(X))
plot3(X,Y,Z)

2.mesh函数&surf函数
mesh函数用于绘制三维网格图
mesh(x,y,z,c)
surf函数用于绘制三维曲面图
surf(x,y,z,c)
一般情况下,默认x,y,z为同型矩阵。其中x,y是网格坐标矩阵,z是网格点上的高度矩阵,c用于指定在不同高度下的曲面的颜色。c省略时,matlab认为c等于z。
![]()
t=-2:0.2:2
[X,Y]=meshgrid(t)
Z=X.*exp(-X.^2-Y.^2)
subplot(1,3,1)
mesh(X,Y,Z)
subplot(1,3,2)
surf(X,Y,Z)
subplot(1,3,3)
plot3(X,Y,Z)
grid on

3.其他形式的mesh函数
3.1 仅带z参数的mesh&surf函数
当x,y省略时,即mesh(z,c)和surf(z,c),把z矩阵的第一维坐标当作y轴坐标,把z矩阵的第二维坐标当作x轴坐标。如下例子
t=1:5
z=[0.5*t;2*t;3*t]
mesh(z)

由图可知,x是z的列下标,y是z的行下标
3.2 带等高线的meshc函数和带底座的meshz函数&
带等高线的surfc函数和带光照效果的surfl函数
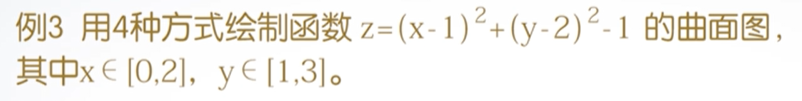
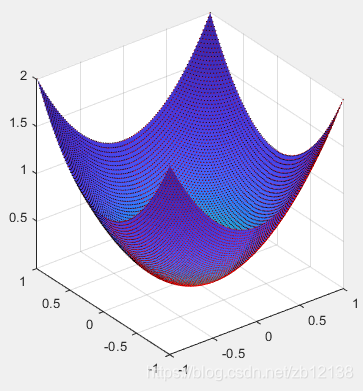
[X,Y]=meshgrid(0:0.1:2,1:0.1:3)
Z=(X-1).^2+(Y-2).^2-1
subplot(2,2,1)
meshc(X,Y,Z);title( '{\bf meshc(x,y,z)}')
subplot(2,2,2)
meshz(X,Y,Z);title('{\bf meshz(x,y,z)}')
subplot(2,2,3)
surfc(X,Y,Z);title('{\bf surfc(x,y,z)}')
subplot(2,2,4)
surfl(X,Y,Z);title('{\bf surfl(x,y,z)}')

由图可知,子图1和3有等高线,子图2有底座,子图4有光照效果
4.标准三维曲面
绘制三维球面sphere和柱面cylinder
[x,y,z]=sphere(n)
sphere函数产生三个n+1阶的方阵,采用这三个矩阵,可以绘制出圆心位于原点和半径为1 的单位球体,参数n决定了球面的光滑程度,默认值为20
[x,y,z]=cylinder(R,n)
R是一个向量,存放柱面各个等间隔间距上的半径,n表示在圆柱体上有n个间隔点,默认有20个间隔点。R是标量时,则绘制圆柱体

subplot(1,3,1)
[x,y,z]=cylinder
surf(x,y,z)
subplot(1,3,2)
t=linspace(0,2*pi,40)
[x,y,z]=cylinder(2+cos(t),30)
surf(x,y,z)
subplot(1,3,3)
[x,y,z]=cylinder(0:0.2:2,30)
surf(x,y,z)

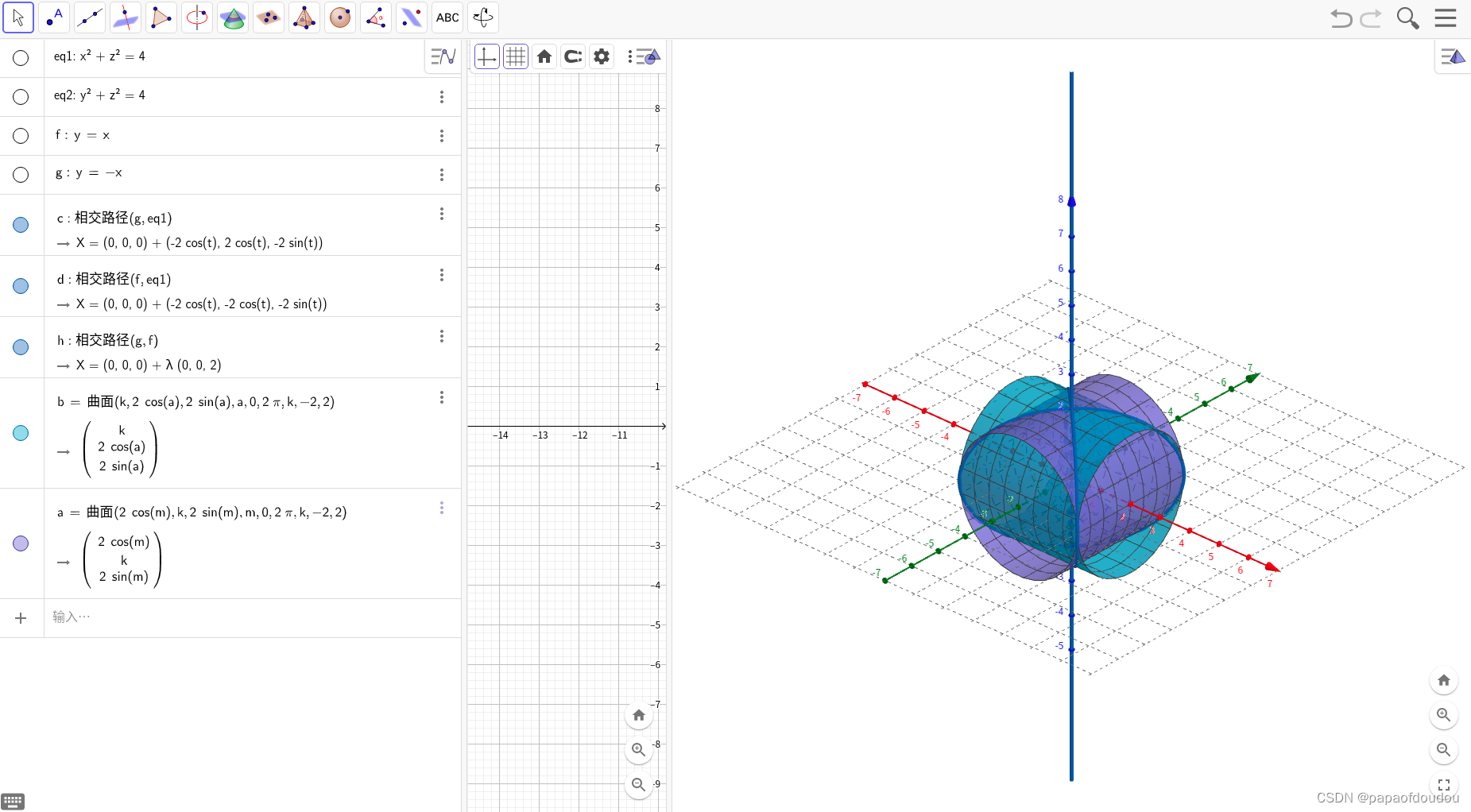
5.fsurf和fmesh函数
如果图形用三个参数方程表示,参数方程有两个变量
fsurf(fx,fy,fz,uvlims)
fmesh(fx,fy,fz,uvlims)
其中,fx,fy,fz代表定义曲面x,y,z坐标的函数通常采用句柄的形式,uvlims为fx,fy,fz自变量的取值范围,用[umin,umax,vmin,vmax]表示,默认为[-5,5,-5,5]
x=@(u,v) u.*sin(v)
y=@(u,v) -u.*cos(v)
z=@(u,v) v %(u,v)!!
fsurf(x,y,z,[-5,5,-2,2])
hold on
fmesh(x,y,z,[-5,5,-2,2])
hold off