前缀和
一维前缀和
s[i]=s[i-1]+a[i]
二维前缀和(子矩阵的和)
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]
差分
一维数组
//b是差分数组b[i]+=c;b[j+1]-=c;
例题

#include<iostream>
using namespace std;
int n,m;
int b[100002],a[100002];
void insert(int i,int j,int c)
{b[i]+=c;b[j+1]-=c;
}
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];insert(i,i,a[i]);}for(int i=1;i<=m;i++){int l,r,c;cin>>l>>r>>c;insert(l,r,c);}for(int i=1;i<=n;i++){a[i]=a[i-1]+b[i];cout<<a[i]<<' ';}
}
二维差分(差分矩阵)
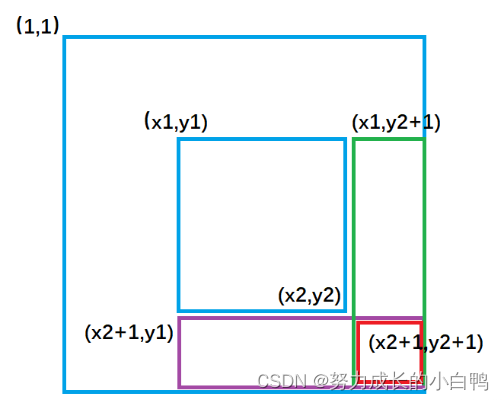
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
例题:

#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}
int main()
{int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j];for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){insert(i, j, i, j, a[i][j]); //构建差分数组}}while (q--){int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1]+b[i][j]; //二维前缀和}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){printf("%d ", a[i][j]);}printf("\n");}return 0;
}字符串的操作STL
#include<string>
string s;
s.size();
s.length();
tolower(a);//将大写字母a,转换为小写字母,返回值是小写字母;a=tolower(a);
字符串
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
using namespace std;
string s[10];//可以读入二维的字符串
int main()
{int n;cin>>n;for(int i=1;i<=n;i++){cin>>s[i];}for(int i=1;i<=n;i++){cout<<s[i]<<endl;}
}
模拟
模拟题可难也可简单,重点是 读懂题意,抽象出来模型(我这说的好像是废话 )
例题(简单)
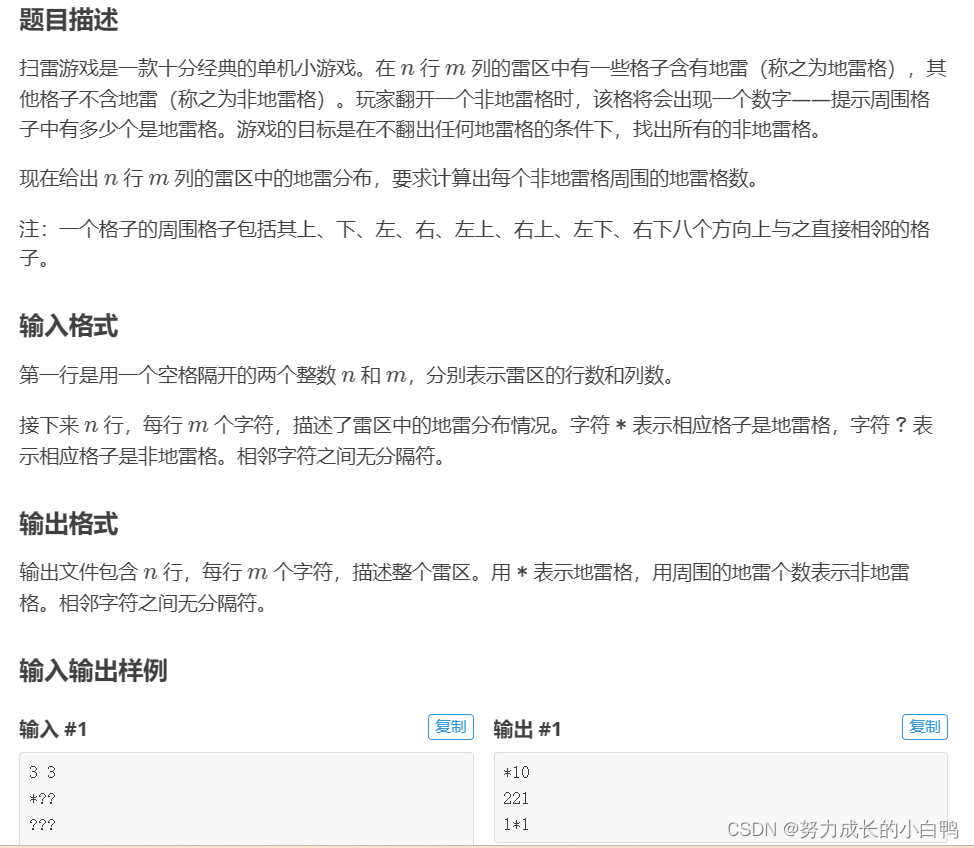
#include <iostream>
#include<string>
using namespace std;
int n,m;
string a[102];
int d[8][2]={{-1,1},{1,-1},{0,1},{0,-1},{1,1},{-1,-1},{1,0},{-1,0}};
int main()
{cin>>n>>m;for(int i=0;i<n;i++){cin>>a[i];}for(int i=0;i<n;i++){for(int j=0;j<m;j++){int ans=0;if(a[i][j]=='*'){cout<<a[i][j];continue;}for(int k=0;k<8;k++){if((i+d[k][0])>=0&&(i+d[k][0]<n)&&(j+d[k][1]>=0)&&j+d[k][1]<m&&a[i+d[k][0]][j+d[k][1]]=='*'){ans++;}}cout<<ans;}cout<<endl;}return 0;
}闰年的判断
bool is_leap(int n)
{if((n%4==0&&n%100!=0)||(n%400==0)){return true;}return false;
}
高精度
高精度加法
例题
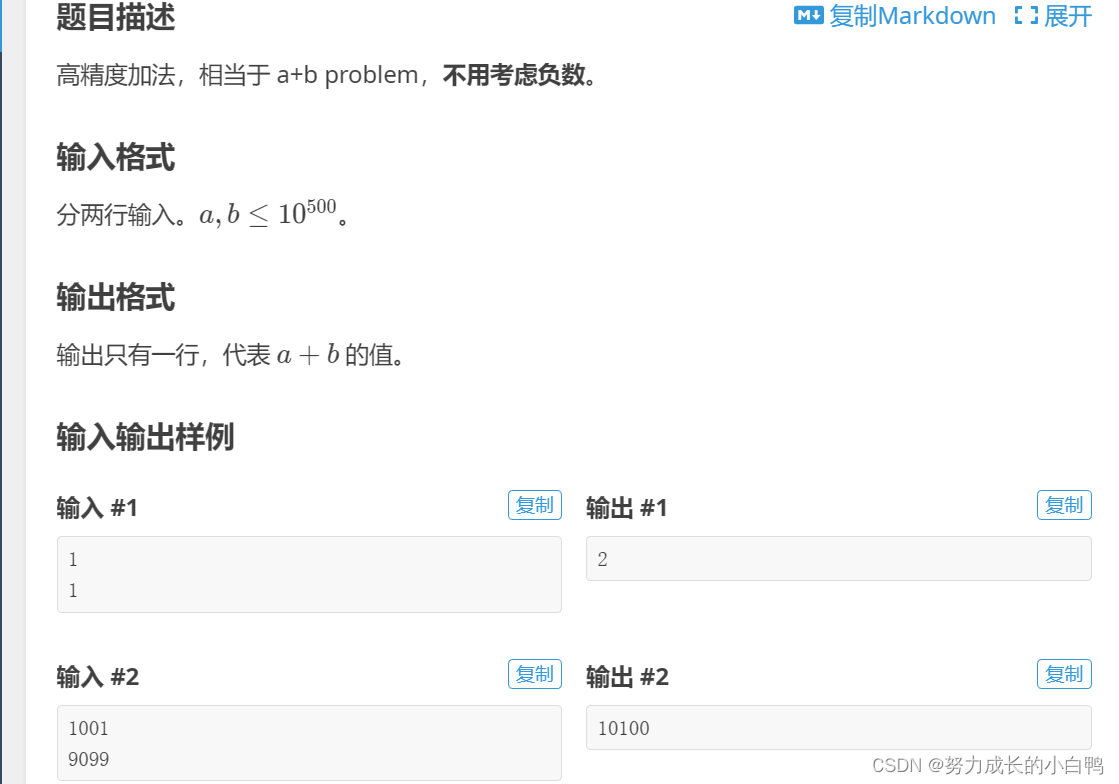
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
vector<int>A,B,C;
string a,b;
void add()
{int t=0;for(int i=0;i<A.size()||i<B.size();i++){if(i<A.size()){t+=A[i];}if(i<B.size()){t+=B[i];}C.push_back(t%10);t=t/10;}if(t){C.push_back(t);}
}
int main()
{cin>>a>>b;for(int i=a.size()-1;i>=0;i--){A.push_back(a[i]-'0');}for(int i=b.size()-1;i>=0;i--){B.push_back(b[i]-'0');}add();for(int i=C.size()-1;i>=0;i--){cout<<C[i];}
}高精度乘法
高精度乘低精度
例题

#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
vector<int>A,B,C;
string a;
int b;
void mul()
{int t=0;for(int i=0;i<A.size();i++){t+=A[i]*b;C.push_back(t%10);t=t/10;}if(t){C.push_back(t);}while(C.size()>1&&C.back()==0){C.pop_back();//把前导零删除}
}
int main()
{cin>>a>>b;for(int i=a.size()-1;i>=0;i--){A.push_back(a[i]-'0');}mul();for(int i=C.size()-1;i>=0;i--){cout<<C[i];}
}高精度乘高精度
例题
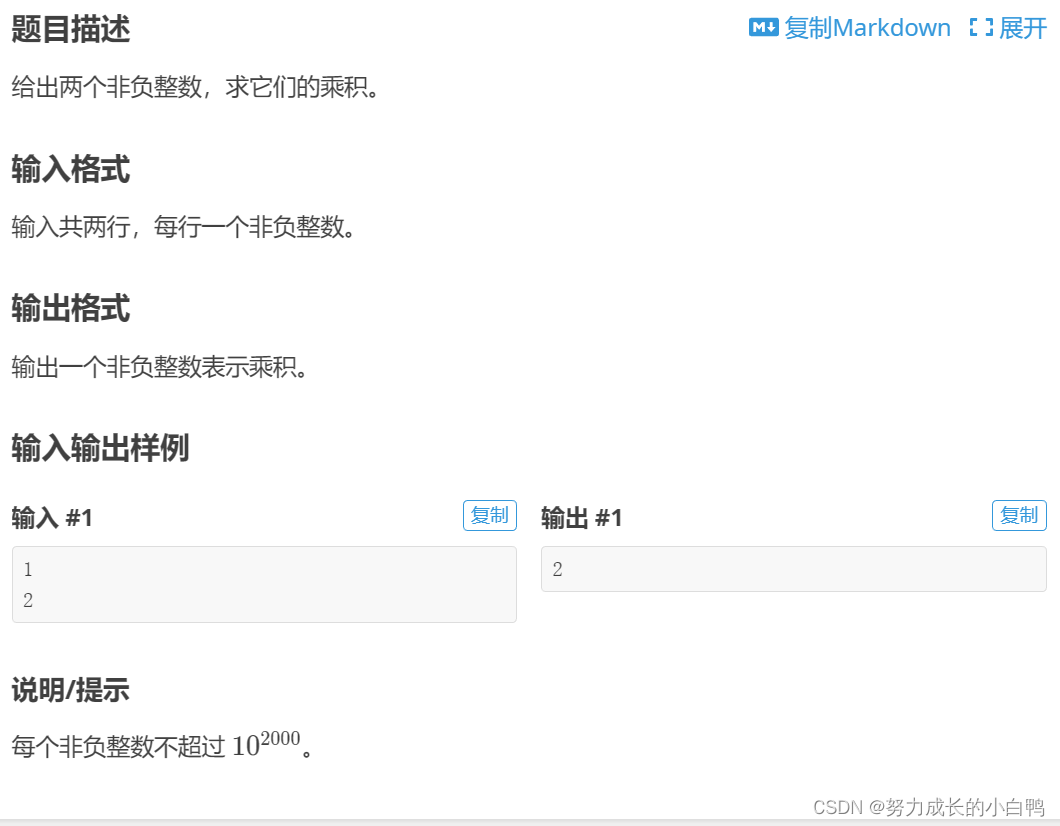
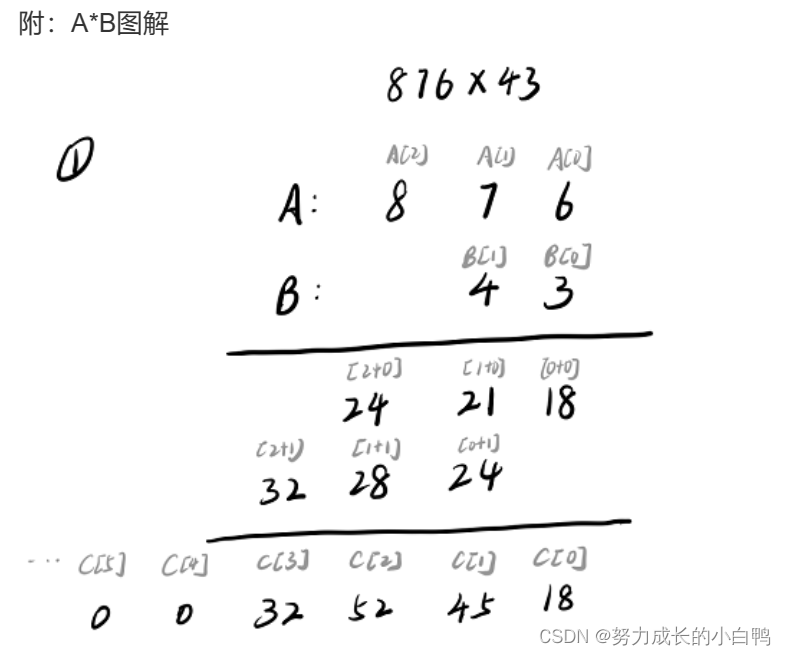
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
vector<int>A,B;
string a,b;
vector<int> mul()
{vector<int>C(A.size()+B.size()+7,0);int t=0;for(int i=0;i<B.size();i++){for(int j=0;j<A.size();j++){C[i+j]+=B[i]*A[j];}}for(int i=0;i<C.size();i++){t+=C[i];C[i]=t%10;t/=10;}if(t){C.push_back(t);}while(C.size()>1&&C.back()==0){C.pop_back();}return C;
}
int main()
{cin>>a>>b;for(int i=a.size()-1;i>=0;i--){A.push_back(a[i]-'0');}for(int i=b.size()-1;i>=0;i--){B.push_back(b[i]-'0');}auto C=mul();for(int i=C.size()-1;i>=0;i--){cout<<C[i];}
}数学知识
卡特兰数
C0 = 1,
C1 = 1, C2 = 2, C3 = 5, C4 = 14, C5 = 42,
C6 = 132, C7 = 429, C8 = 1430, C9 = 4862, C10 = 16796,
C11 = 58786, C12 = 208012, C13 = 742900, C14 = 2674440, C15 = 9694845,
C16 = 35357670, C17 = 129644790, C18 = 477638700, C19 = 1767263190, C20 = 6564120420, ...递推公式
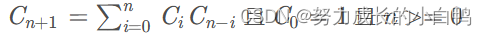
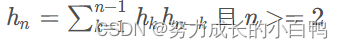
#include <iostream>
#include<algorithm>
using namespace std;
//卡特兰数,用的是第二个公式
const int n=10;
int c[n];
int main()
{c[1]=1,c[2]=1;for(int i=3;i<=n;i++){for(int j=1;j<i;j++){c[i]+=c[j]*c[i-j];}}for(int i=1;i<=n;i++){printf("c[%d]=%d\n",i,c[i]);}return 0;
}
相关题目练习可以参考这位大佬的总结
组合数学
例题

#include<iostream>
using namespace std;
int n;
const int mod=1e9+7;
const int N = 2004;
int c[2004][2004];int a,b;
void init()
{for(int i=0;i<N;i++){for(int j=0;j<=i;j++){if(!j){c[i][j]=1;}else{c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;}}}
}
int main()
{cin>>n;init();while(n--){scanf("%d%d",&a,&b);cout<<c[a][b]<<endl;}
}
例题

#include <iostream>//只有70分,不过是绿题啊,第一次做绿题,所以这种数学知识,如果没见过就超级难,一旦学过也就还好。using namespace std;
const int N=2e3+3;
long long t,k;
unsigned long long c[N][N];
void cal()
{c[0][0]=0;for(int i=0;i<=2000;i++){for(int j=0;j<=i;j++){if(j==0){c[i][j]=1;}else{c[i][j]=c[i-1][j]+c[i-1][j-1];}}}
}
int main()
{long long ans=0;cal();cin>>t>>k;int a,b;while(t--){scanf("%d%d",&a,&b);for(int i=0;i<=a;i++){for(int j=0;j<=min(i,b);j++){// cout<<c[i][j]<<' ';if(c[i][j]%k==0){ans++;}}}cout<<ans<<endl;ans=0;}return 0;
}素数筛(欧拉筛)
bool st[N];//st[i]为1,说明被筛掉了,也就是说,不是素数
int cnt=0;
for(int i=2;i<=n;i++)
{if(!st[i]){primes[cnt++]=i;for(int j=i+i;j<=n;j+=i){st[j]=1;}}
}例题

#include <iostream>using namespace std;
const int N = 1e8+2;
bool st[N];
int primes[N];
int cnt;
int n,m;
void is_primes()
{for(int i=2;i<=n;i++){if(!st[i]){cnt++;primes[cnt]=i;for(int j=i+i;j<=n;j+=i){st[j]=1;}}}
}//TLE,只有四十分,埃氏筛效率还是低了些。1e8会TLE,例如一个数 24,它会被 2, 3, 4 三个数标记,这就重复了两次,更大的数同理。
int main()
{cin>>n>>m;int q;is_primes();while(m--){scanf("%d",&q);printf("%d\n",primes[q]);}return 0;
}线性筛
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] <= n / i; j ++ ){st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}
质因子分解
定理:一个合数可以由多个比他小的质数相乘而得,而这些质数就是他的质因数。
//要计算的是从1到n之间的所有合数的质因数
for(int i=1;i<=n;i++)
{int x=i;if(!st[x])//没有被筛掉,也就是是合数{continue;}else{for(int j=2;j<=x;j++){while(x%j==0){p[cnt++]=j;//p数组中存的是质因数x=x/j;}}}
}
用map实现
例题

#include<iostream>
#include<map>
using namespace std;
void fen(int n)
{map<int,int> m;for(int i=2;i<=n/i;i++){if(n%i==0){int c=0;while(n%i==0){c++;n=n/i;}m[i]+=c;}}if(n>=2)//加上大于根号n的素因子{m[n]++;}map<int,int>::iterator iter;for(iter=m.begin();iter!=m.end();iter++){printf("%d %d\n",iter->first,iter->second);}cout<<endl;
}
int main()
{int n,a;cin>>n;while(n--){scanf("%d",&a);fen(a);}return 0;
}
约数个数定理

套用上面map实现的代码
void fen(int n)
{map<int,int> m;for(int i=2;i<=n/i;i++){if(n%i==0){int c=0;while(n%i==0){c++;n=n/i;}m[i]+=c;}}if(n>=2)//加上大于根号n的素因子{m[n]++;}map<int,int>::iterator iter;for(iter=m.begin();iter!=m.end();iter++){//printf("%d %d\n",iter->first,iter->second);res*=(iter->second+1);//这里}cout<<endl;
}
分离整数
while(n)
{a.push_back(n%10);//依次存储的是个位 十位等n=n/10;
}
例题
得到各个位数
//前三位
int n=1234567;
int x=n/10000;
//取后两位
int y=n%100;
进制转换
#include<iomanip>
setbase(n)
//hex十六进制,oct八进制,dec十进制
最大公约数
int gcd(int a,int b)
{return b==0?a:gcd(b,a%b);
}
例题
这个例题中,主要是字符串的操作,最大公约数只是其中的一个应用,但是如果不会最大公约数和最小公倍数的话,也会很麻烦

#include<cstdio>
#include<iostream>
using namespace std;
int a,b,c,d;
int gcd(int x,int y)
{if(y==0)return x;return gcd(y,x%y);
}
int main()
{scanf("%d/%d",&a,&b);//这一步就很巧妙while(scanf("%d/%d",&c,&d)!=EOF)//EOF是先按Enter键,然后是Ctrl+z{int m=(b*d)/gcd(b,d);//最小公倍数*最大公约数=a*ba=a*(m/b)+c*(m/d);b=m;int x=gcd(a,b);a=a/x;b=b/x;//cout<<a<<'/'<<b<<endl;}if(b<0){a=-a;b=-b;}if(b==1)printf("%d\n",a);elseprintf("%d/%d\n",a,b);return 0;
}快速幂运算
例题

ps:十年OI一场空,不开long long见祖宗
附上数据范围
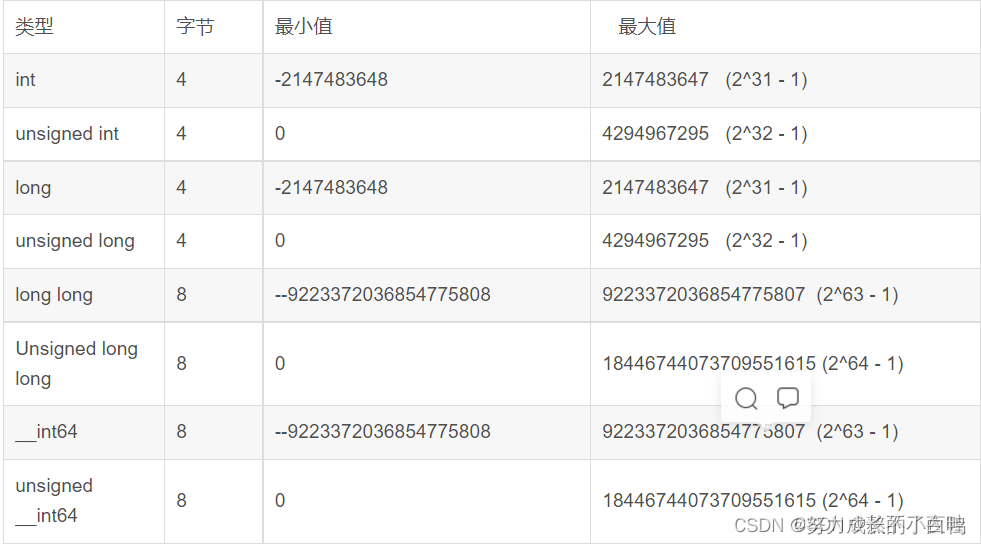
#include <iostream>using namespace std;
long long a,b,p;
int n;
typedef long long ll;
ll qmi(ll a,ll b,ll q)
{ll res=1;while(b){if(b&1){res=((res%p)*(a%p))%p;}b>>=1;a=(a*a)%p;}return res;
}
int main()
{cin>>n;while(n--){cin>>a>>b>>p;cout<<qmi(a,b,p)<<endl;}return 0;
}贪心算法
取当前情况最好的,贪心不贪,重点在于排序加模拟。
例题
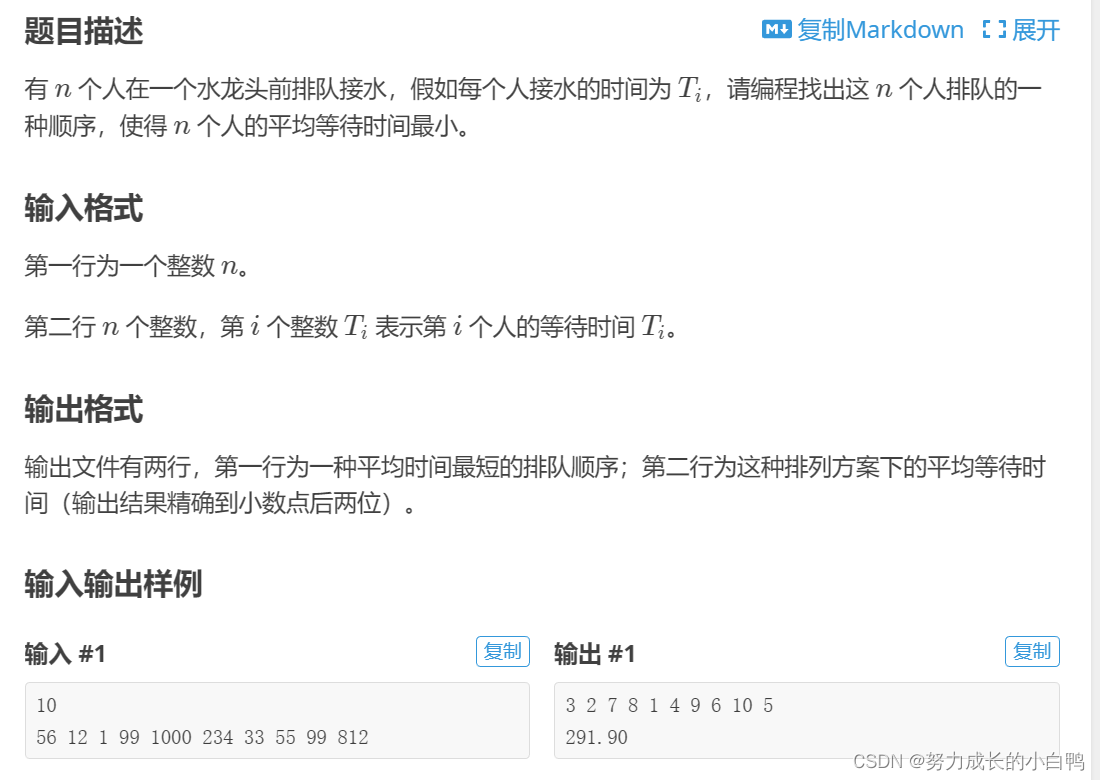
思路:等待时间最小,就是让接水时间最短的人先接。用sort排个序,因为是要输出排队的序号,所以就用pair了
#include <iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int n;
int sum[1002];
pair<int,int>a[1002];
bool cmp(pair<int,int>x,pair<int,int>y)
{return x.second < y.second;
}
int main()
{cin>>n;for(int i=1;i<=n;i++){a[i].first=i;cin>>a[i].second;}sort(a+1,a+n+1,cmp);for(int i=1;i<=n;i++){cout<<a[i].first<<' ';}cout<<endl;memset(sum,0,sizeof(sum));for(int i=2;i<=n;i++){sum[i]=sum[i-1]+a[i-1].second;}double ans;for(int i=2;i<=n;i++){ans+=sum[i];}ans=ans*1.0/n;printf("%.2lf",ans);return 0;
}例题
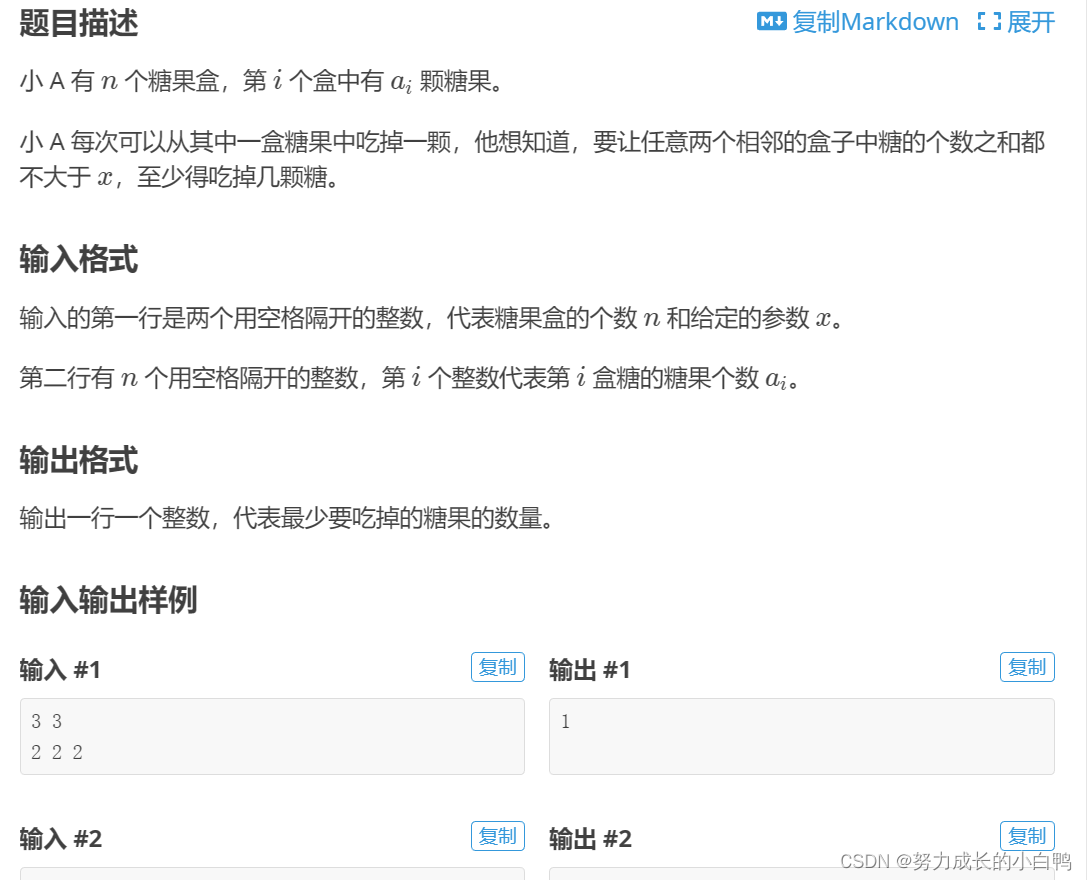
思路:贪心就是取当前情况最好的。在这道题中,正向遍历,如果两者之和大于x,就吃掉a[i]中的,如果a[i]为0了,就吃掉a[i-1]中的糖果。因为后面还有,如果先吃掉a[i-1]中的,对后面没啥影响,所以不是最好的情况。(至于理论证明为啥这样最好,本蒟蒻不会5555)
#include <iostream>
#include<algorithm>
#include<cmath>
using namespace std;
long long n,x;
long long a[100004];
int main()
{cin>>n>>x;for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}long long t=0;long long ans=0;long long temp=0;for(int i=2;i<=n;i++){if(a[i-1]+a[i]>x){temp=a[i];t=a[i-1]+a[i]-x;ans+=t;a[i]=a[i]-t;if(a[i]<0){a[i]=0;a[i-1]=a[i-1]-(x-temp);//开始吃a[i-1]中的糖果}}}cout<<ans<<endl;return 0;
}
例题:
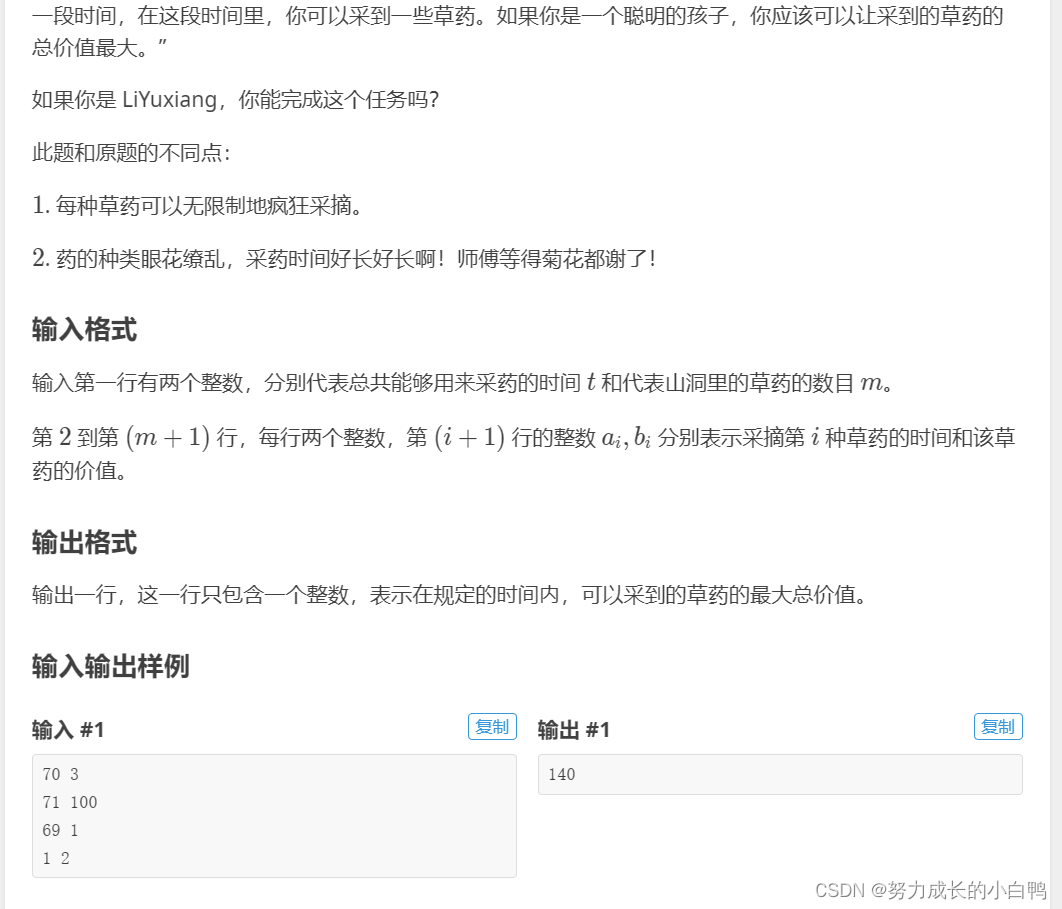
思路:这道题的标签是动态规划,但是数据范围有点大,而且俺也不会完全背包问题,及啥滚动数组,就用贪心做了,but只有90分。哭辽
#include <iostream>
#include<algorithm>
using namespace std;
int t,m;
const int N =1e4+2;
pair<int,int> p[N];
int d[N][N];
bool cmp(pair<int,int>x,pair<int,int>y)
{return (x.second*1.0/x.first) > (y.second*1.0/y.first);
}
int main()
{cin>>t>>m;int a,b;for(int i=0;i<m;i++){cin>>a>>b;p[i].first=a;p[i].second=b;}sort(p,p+m,cmp);long long cost=t;long long val=0;//十年 OI 一场空,不开 long long 见祖宗。for(int i=0;i<m;i++){while(cost>0){val+=p[i].second;cost-=p[i].first;}if(cost<0){cost+=p[i].first;val-=p[i].second;}if(cost==0){break;}}cout<<val;return 0;
}动态规划
格式化输出
//在C++中,cout<<int(2.56);输出就是2,只保留整数部分,如果要四舍五入,就要加上0.5
//可以用printf("%.2lf",2.56);自动进行四舍五入。此外,printf("%02d",6);表示输出占两位,不足两位添加前导0
STL
贴个大佬总结的STL食用指南
//自定义排序方式
bool cmp(int x,int y)
{return x>y;
}//表示按照从大到小的方式进行。这种定义方式,在pair或者结构体中使用范围更广
//例如
bool cmp(pair<int,int>x,pair<int,int>y)
{return x.first > y.first;
}//按照first的值升序排列;
//需要包含在头文件algorithm中
sort(a,a+n,cmp);//a为普通数组
sort(a,a+n,greater<int>());//降序,默认是升序
sort(a.begin(),a.end());//a为vector数组
reverse函数
用法示例(vector和数组)
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
int main()
{vector<int> vec;int a[10];int n;cin>>n;for(int i=0;i<n;i++){int c;cin>>c;vec.push_back(c);a[i]=c;}reverse(vec.begin(),vec.end());reverse(a,a+n);cout<<"vec"<<endl;for(int i=0;i<n;i++){cout<<vec[i]<<' ';}cout<<endl;cout<<"数组a"<<endl;for(int i=0;i<n;i++){cout<<a[i]<<' ';}cout<<endl;
}
去重(要求序列是有序的,首先用sort排序)
v.erase(unique(v.begin(),v.end()),v.end());
优先队列
priority_queue<Type, Container, Functional>set
map
桶计数是map一个功能之一
#include<bits/stdc++.h>
using namespace std;
map<int,int>book;
int n;
int main()
{cin>>n;for(int i=1;i<=n;i++){int temp;cin>>temp;book[temp]++;}int k;cin>>k;cout<<book[k]<<endl;return 0;
}
二分查找
binary_search(起始地址,结束地址,要查找的数值)
返回值是 是否存在这么一个数,是一个bool值。
binary_search(a,a+n,3);
lower_bound(起始地址,结束地址,要查找的数值),返回值就是返回第一次出现大于等于那个要查找的数的地址;如果不存在则返回a.end()
lower_bound(a,a+n,3)-a;
upper_bound(起始地址,结束地址,要查找的数值)返回的是被查序列中第一个大于查找的数的指针;,如果不存在则返回a.end()
upper_bound(a,a+n,3)-a;
综合应用
查询某个元素出现的次数
upper_bound - lower_bound
upper_bound(a,a+n,3)-lower_bound(a,a+n,3);
例题

#include <iostream>
#include<algorithm>
using namespace std;
int n,c;
const int N = 2e5+5;
int a[N];
int main()
{cin>>n>>c;for(int i=1;i<=n;i++){scanf("%d",&a[i]);}sort(a+1,a+n+1);long long ans=0;//没开long long,只有90分//int posg=upper_bound(a+1,a+n+1,c)-a;这是之前的思路,只有76分for(int i=1;i<=n;i++){//cout<<"a[i"<<a[i]<<endl;ans+=(upper_bound(a+1,a+n+1,a[i]+c))-(lower_bound(a+1,a+1+n,a[i]+c));}cout<<ans<<endl;return 0;
}例题
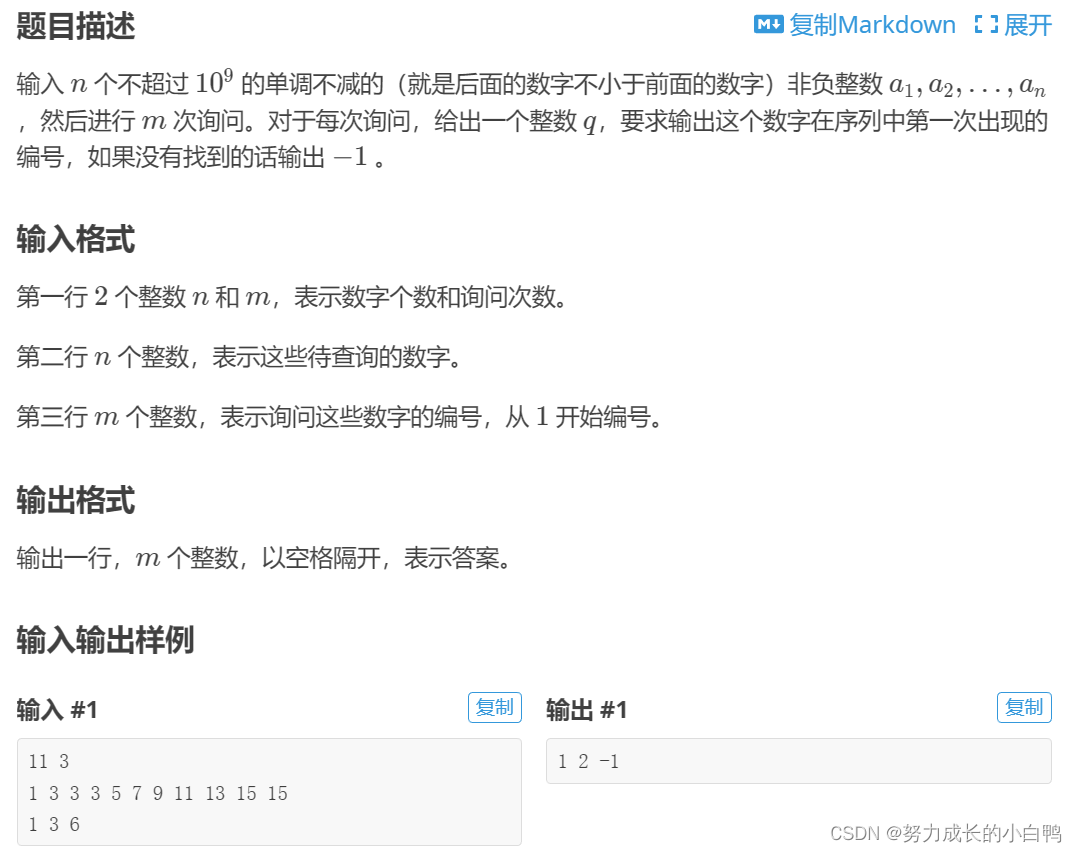
#include <iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 1e6+3;
int a[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){scanf("%d",&a[i]);}int q;while(m--){cin>>q;if(!binary_search(a+1,a+1+n,q)){cout<<-1<<' ';}else{int x=lower_bound(a+1,a+1+n,q)-a;cout<<x<<' ';}}return 0;
}动态规划
考虑小规模。思考的时候,是由n-1推n,由n-2推n-1;写方程的时候,从1推2,推n
背包问题
0-1背包问题
例题
有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。第 i件物品的体积是 vi,价值是 wi。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
0-1背包(朴素版)
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N=1005;
int v[N],w[N],f[N][N];//f[i][j]表示背包容量为j时前i个物品的最大价值
int main()
{cin>>n>>m;//读入物品的数量和背包容量for(int i=1;i<=n;i++){cin>>v[i]>>w[i];//读入每个物品的重量和价值}//dpfor(int i=1;i<=n;i++){for(int j=0;j<=m;j++){if(j<v[i])f[i][j]=f[i-1][j];//如果背包容量小于物品的重量,那就不装else{f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i])//如果背包容量大于物品的重量,这时候就有两种选择,装或者不装,如果装入的话,j就要减去第i个物品的重量,这两种情况取其中的最大值}}}cout<<f[n][m]<<endl;return 0;
0-1背包(升级版)
解释:由于进行状态转移的过程中只用到了上一层的数据,所以可以进行降维。
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 1e3+5;
int f[N],v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=m;j>=v[i];j--){ f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m]<<endl;return 0;
}
完全背包问题(朴素版)
完全背包问题和0-1背包问题的区别就是每一种物品的个数是无限的。
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 2e3+5;
int f[N][N],v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;v[i]*k<=j;k++){if(j<v[i]){f[i][j]=f[i-1][j];}else{f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);}}}}cout<<f[n][m]<<endl;return 0;
}
优化版
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 2e3+5;
int f[N][N],v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);}}cout<<f[n][m]<<endl;return 0;
}
完全背包(再升级版)
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 2e3+5;
int f[N],v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=v[i];j<=m;j++){f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m]<<endl;return 0;
}
多重背包(朴素版)
#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N = 110;
int f[N][N],v[N],w[N],s[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i]>>s[i];}for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k<=s[i]&&k*v[i]<=j;k++){f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);}}}cout<<f[n][m]<<endl;return 0;
}
搜索bfs
使用队列,queue
例题
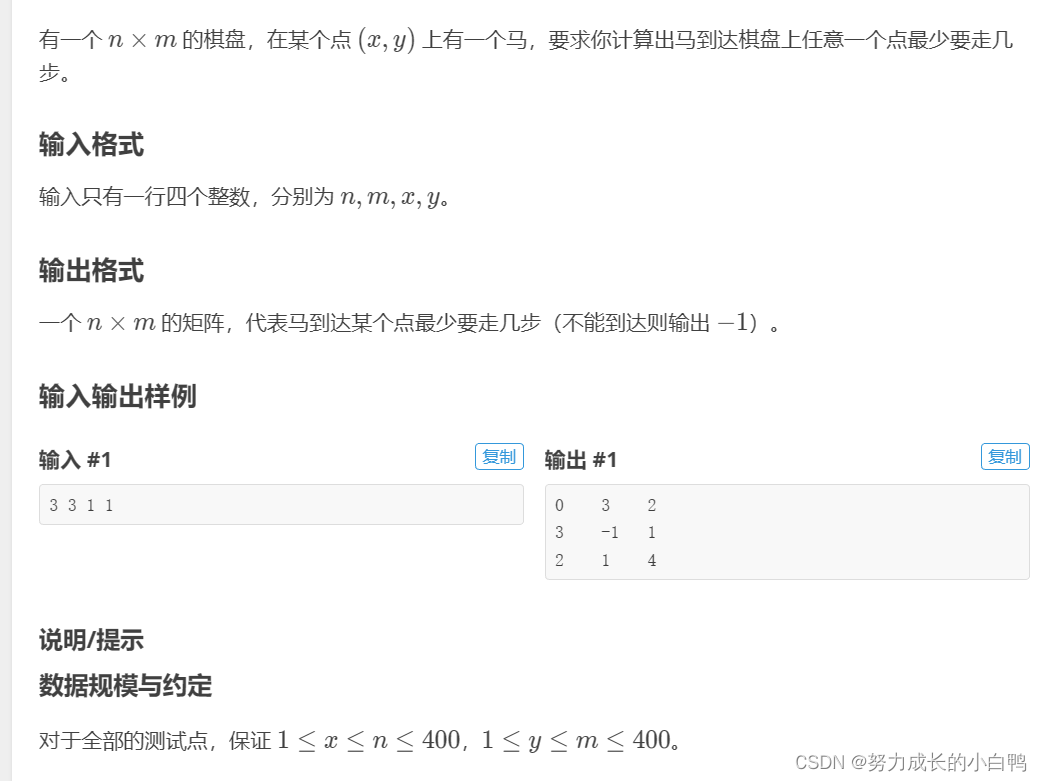
思路:本来想用最短路算法,迪杰斯特拉,看到题目标签是bfs,就用了bfs,我是菜鸡,呜呜。这题用pair正好。
#include <iostream>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
queue<PII>q;
const int N = 405;
int mp[N][N];
int d[8][2]={{1,-2},{1,2},{2,-1},{2,1},{-1,-2},{-1,2},{-2,-1},{-2,1}};
int vis[N][N];
int dis[N][N];
int n,m,x,y;
void bfs(int x,int y)
{PII temp;temp.first=x;temp.second=y;q.push(temp);vis[temp.first][temp.second]=1;while(!q.empty()){temp=q.front();q.pop();//vis[temp.first][temp.second]=0;此处不需要写,否则会死循环for(int i=0;i<8;i++){int tx,ty;tx=temp.first+d[i][0];ty=temp.second+d[i][1];if(tx>=0&&tx<n&&ty>=0&&ty<m&&!vis[tx][ty]){q.push(make_pair(tx,ty));vis[tx][ty]=1;dis[tx][ty]=dis[temp.first][temp.second]+1;}}}
}
int main()
{cin>>n>>m>>x>>y;bfs(x-1,y-1);for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(dis[i][j]==0){if(i==x-1&&j==y-1){cout<<0<<' ';}else{cout<<-1<<' ';}}else{cout<<dis[i][j]<<' ';}}cout<<endl;}return 0;
}
dfs
搞清楚状态转移
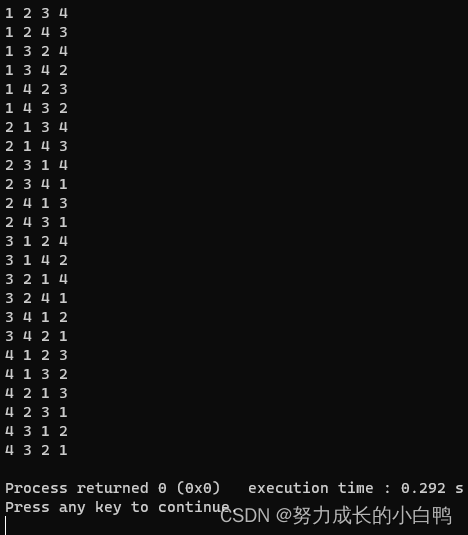
全排列问题
//头文件algorithm
int a[4]={1,2,3,4};
do
{for(int i=0;i<4;i++){cout<<a[i]<<' ';}cout<<endl;
}while(next_permutation(a,a+4));
图的基本应用
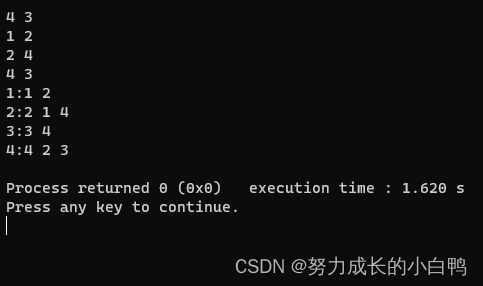
邻接表(用vector实现)
#include <iostream>
#include<vector>
#include<queue>
using namespace std;
const int N=1e5+3;
int vis[N];
vector<int>v[N];
queue<int> q;
int main()
{int n,m;cin>>n>>m;int a,b;for(int i=1;i<=n;i++){v[i].push_back(i);}for(int i=0;i<m;i++){cin>>a>>b;v[a].push_back(b);v[b].push_back(a);}for(int i=1;i<=n;i++){int len=v[i].size();int maxx=0;cout<<i<<':';for(int j=0;j<len;j++){cout<<v[i][j]<<' ';}//cout<<maxx<<' ';cout<<endl;}return 0;
}
单源最短路径
迪杰斯特拉算法
例题同下(这个算法不是靠队列实现的)
依然只有60分,因为我用的还是邻接矩阵
#include <iostream>
#include<cstring>
using namespace std;
const int N=1e4;
const int INF=0x3f;
int mp[N][N];
int vis[N];
int dis[N];
int n,m,s;
void dijstra(int s)
{dis[s]=0;//vis[s]=1;while(1){int min_=INF,mini=0;for(int j=1;j<=n;j++){if(dis[j]<min_&&!vis[j])//寻找没有确定为最短路径的点{min_=dis[j];mini=j;}}if(mini==0){break;//没有找到就退出}vis[mini]=1;for(int i=1;i<=n;i++){if(dis[i]>dis[mini]+mp[mini][i]){dis[i]=dis[mini]+mp[mini][i];//依次进行松弛}}}
}
int main()
{memset(mp,INF,sizeof(mp));memset(dis,INF,sizeof(dis));cin>>n>>m>>s;int a,b,w;while(m--){cin>>a>>b>>w;mp[a][b]=min(mp[a][b],w);}dijstra(s);for(int i=1;i<=n;i++){cout<<dis[i]<<' ';}return 0;
}spfa算法:可以判断是否会存在负权边
例题
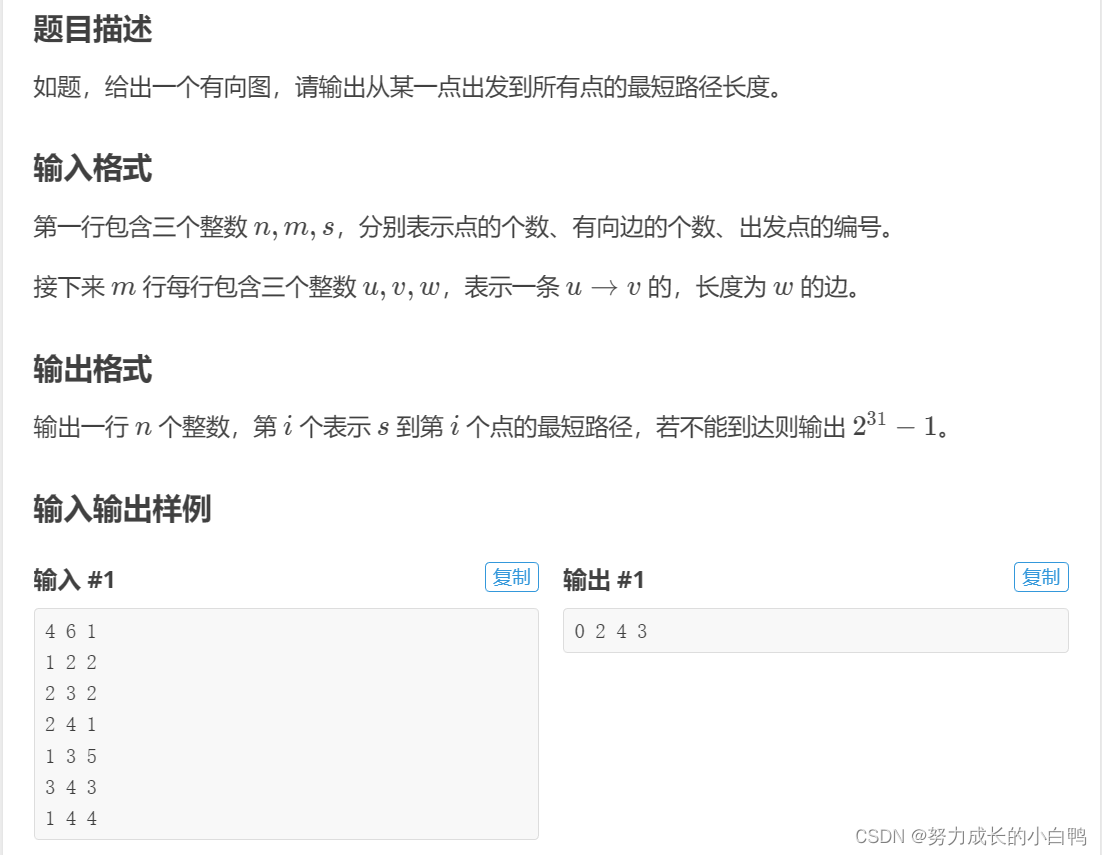
邻接矩阵版本(会MLE,只有60分)
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
int n,m,s;
const int N = 1e3+2;
const int INF=0x3f;
int mp[N][N];
queue<int> q;
int sum[N];
int dis[N],vis[N];
int cur;
void spfa(int s)
{q.push(s);vis[s]=1;dis[s]=0;while(!q.empty()){cur=q.front();q.pop();vis[cur]=0;for(int i=1;i<=n;i++){if(mp[cur][i]!=INF){if(dis[i]>dis[cur]+mp[cur][i]){dis[i]=dis[cur]+mp[cur][i];if(vis[i]!=1){q.push(i);vis[i]=1;/*sum[i]++;if(sum[i]>=n){cout<<"有负权回路"<<endl;}*/}}}}}}
int main()
{cin>>n>>m>>s;int a,b,w;memset(dis,INF,sizeof(dis));memset(mp,INF,sizeof(mp));for(int i=1;i<=m;i++){cin>>a>>b>>w;mp[a][b]=min(mp[a][b],w);}spfa(s);for(int i=1;i<=n;i++){cout<<dis[i]<<' ';}
}邻接表版
并查集
例题

无路径压缩版本
(会TLE)
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
int n,m;
int f[100002];
int find_(int x)
{if(x!=f[x]){find_(f[x]);}elsereturn f[x];
}
int main()
{cin>>n>>m;char op;int a,b;for(int i=1;i<=n;i++){f[i]=i;}while(m--){cin>>op;cin>>a>>b;if(op=='M'){a=find_(a);b=find_(b);if(a!=b){f[a]=b;}}if(op=='Q'){if(find_(a)==find_(b)){cout<<"Yes"<<endl;}else{cout<<"No"<<endl;}}}return 0;
}路径压缩版
#include <iostream>
#include<algorithm>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
int n,m;
int f[100002];
int find_(int x)
{if(x==f[x]){return f[x];}else{f[x]=find_(f[x]);//这里return f[x];}}
void merge_(int a,int b)
{f[find_(a)]=find_(b);
}
int main()
{cin>>n>>m;char op;int a,b;for(int i=1;i<=n;i++){f[i]=i;}while(m--){cin>>op;cin>>a>>b;if(op=='M'){if(find_(a)!=find_(b))merge_(a,b);}if(op=='Q'){if(find_(a)==find_(b)){cout<<"Yes"<<endl;}else{cout<<"No"<<endl;}}}return 0;
}一些注意事项
1.要记得 long long;
2.实现估算一下,如果循环次数超过10e8就要考虑进行优化,否则可能会TLE;
3.二维数组如果大于10e5可能会MLE,要考虑优化;
4.x%n的值为0到n-1;
5.EOF可以用不?
准备了近一个月。
尽人事,听天命吧。
事实证明,会这些基本的算法是不配参加蓝桥杯的 (赛后补充)
含泪捐了300元
附大佬总结的2016年真题