复杂数据结构(1)
1. Splay
基本概念
什么是 Splay
Splay 是一种二叉查找树,它通过不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,并且保持平衡而不至于退化为链.
旋转操作
为了使 Splay 保持平衡而进行旋转操作,旋转的本质是将某个节点上移一个位置。
旋转需要保证
- 整棵 Splay 的中序遍历不变(不能破坏二叉查找树的性质)。
- 受影响的节点维护的信息依然正确有效。
- root 必须指向旋转后的根节点。
在 Splay 中旋转分为两种:左旋和右旋。
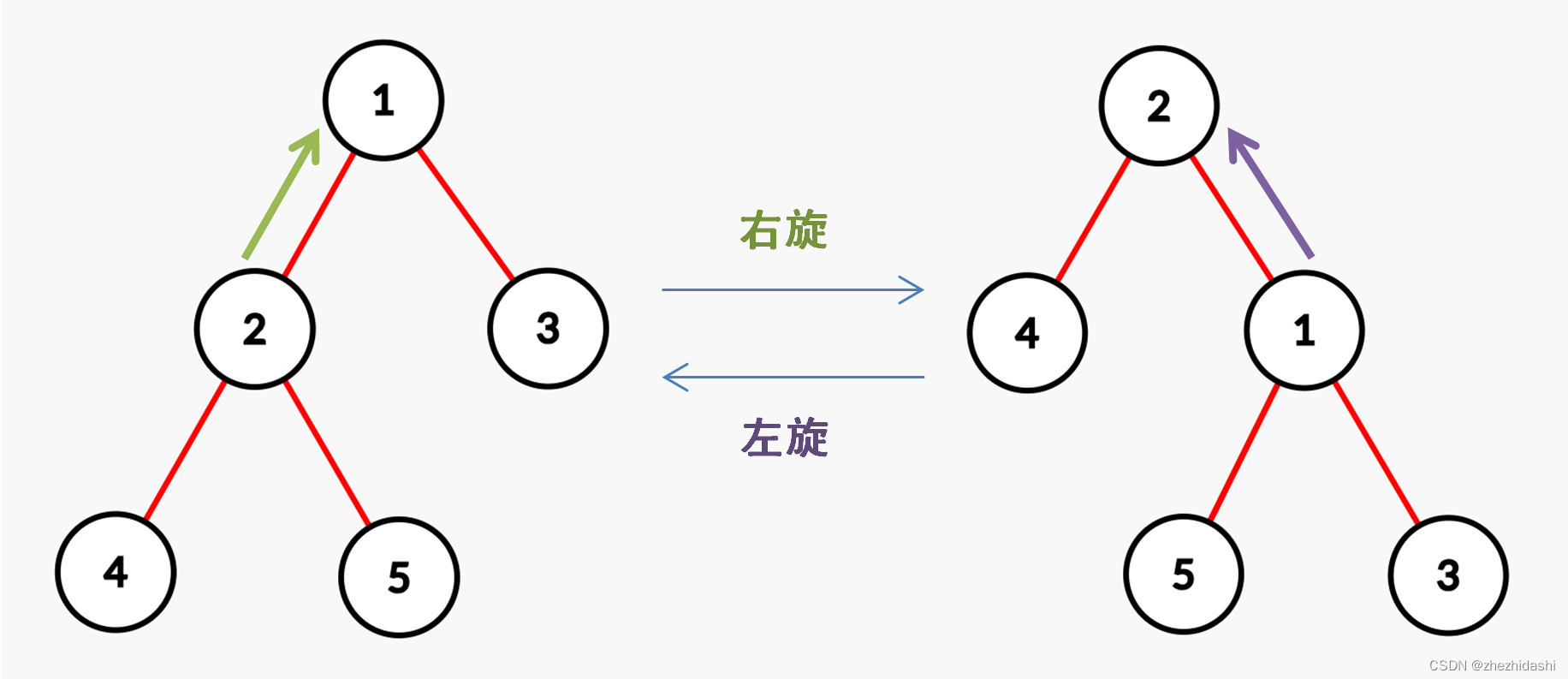
具体分析旋转步骤 (假设需要旋转的节点为 xxx,其父亲为 yyy,以右旋为例)
- 将 yyy 的左儿子指向 xxx 的右儿子,且 xxx 的右儿子的父亲指向 yyy。
ch[y][0]=ch[x][1]; fa[ch[x][1]]=y; - 将 的右儿子指向 ,且 的父亲指向 。
ch[x][chk^1]=y; fa[y]=x; - 如果原来的 还有父亲 ,那么把 的某个儿子(原来 所在的儿子位置)指向 ,且 的父亲指向 。
fa[x]=z; if(z) ch[z][y==ch[z][1]]=x;
Splay 操作
Splay 规定:每访问一个节点后都要强制将其旋转到根节点。此时旋转操作具体分为 666 种情况讨论(其中 xxx 为需要旋转到根的节点)
- 如果 xxx 的父亲是根节点,直接将 xxx 左旋或右旋(图 1,21,21,2)。
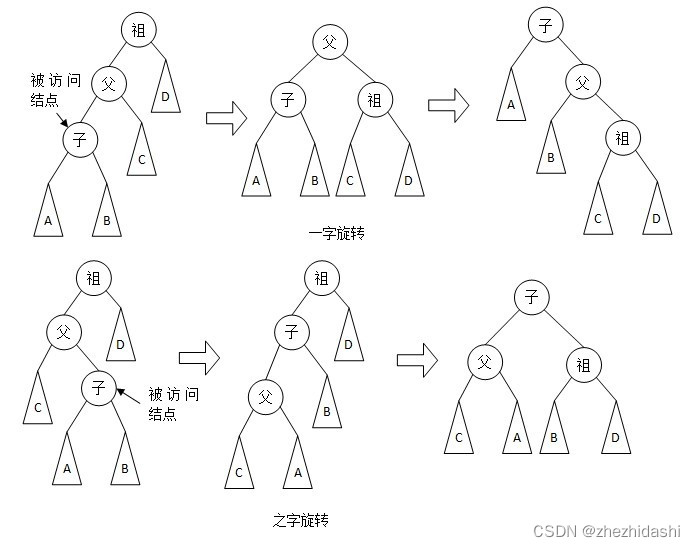
- 如果 xxx 的父亲不是根节点,且 xxx 和父亲的儿子类型相同,首先将其父亲左旋或右旋,然后将 xxx 右旋或左旋(图 3,43,43,4)。
- 如果 xxx 的父亲不是根节点,且 xxx 和父亲的儿子类型不同,将 xxx 左旋再右旋、或者右旋再左旋(图 5,65,65,6)。
- Splay 不一定能保证左子树都小于根节点,右子树都大于根节点;但是可以保证中序遍历的顺序就是原序列的顺序。因为 Splay 可以像线段树一样维护一个无序序列。当然,如果该序列本身是有序的,那么 Splay 就是一个平衡二叉树,左子树小于根节点,右子树大于根节点。
- rotate 示意图
950. 郁闷的出纳员
- 题意:n表示下面有多少条命令,min表示工资下界。有四种命令
I命令,格式为I_k,表示新建一个工资档案,初始工资为 kkk。如果某员工的初始工资低于工资下界,他将立刻离开公司. 即离开公司的员工的总数不算这个.A命令,格式为A_k,表示把每位员工的工资加上 kkk.S命令,格式为S_k,表示把每位员工的工资扣除 kkk.F命令,格式为F_k,表示查询第 kkk 多的工资.
- 对于每条
F命令,你的程序要输出一行,仅包含一个整数,为当前工资第 kkk 多的员工所拿的工资数,如果 kkk 大于目前员工的数目,则输出-1。输出文件的最后一行包含一个整数,为离开公司的员工的总数。
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 100010, INF = 1e9;
int N, M;
struct node {int s[2], p, v;int size;void init(int v_, int p_) {v = v_, p = p_;size = 1;}
}tr[maxn];
int root, idx;
int tot, delta;void pushup(int x) {tr[x].size = tr[tr[x].s[0]].size + tr[tr[x].s[1]].size + 1;
}void rotate(int x) {int y = tr[x].p, z = tr[y].p;int k = (tr[y].s[1] == x);tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;tr[x].s[k ^ 1] = y, tr[y].p = x;pushup(y), pushup(x);
}void splay(int x, int k) {while (tr[x].p != k) {int y = tr[x].p, z = tr[y].p;if (z != k) {if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);else rotate(y);}rotate(x);}if (!k) root = x;
}int insert(int v) {int u = root, p = 0;while (u) p = u, u = tr[u].s[v > tr[u].v];u = ++idx;if (p) tr[p].s[v > tr[p].v] = u;tr[u].init(v, p);splay(u, 0);return u;
}
//大于等于v的最小的节点的编号
int get(int v) {int u = root, res;while (u) {if (tr[u].v >= v) res = u, u = tr[u].s[0];else u = tr[u].s[1];}return res;
}
//找到这个有序序列第 k 个数(算上两个哨兵)
int get_k(int k) {int u = root;while (u) {if (tr[tr[u].s[0]].size >= k) u = tr[u].s[0];else if (tr[tr[u].s[0]].size + 1 == k) return tr[u].v;else k -= tr[tr[u].s[0]].size + 1, u = tr[u].s[1];}return -1; //找不到
}
int main() {scanf("%d%d", &N, &M);int L = insert(-INF), R = insert(INF);while (N--) {char op[2];int k;scanf("%s%d", op, &k);if (op[0] == 'I') {if (k >= M) {//k 需要减 delta,因为默认的是所有人的工资都加上了deltak -= delta, insert(k), tot++;}}else if (op[0] == 'A') {delta += k;}else if (op[0] == 'S') {delta -= k;R = get(M - delta);splay(R, 0), splay(L, R);tr[L].s[1] = 0;pushup(L), pushup(R);}else {if (tr[root].size - 2 < k) printf("-1\n");else printf("%d\n", get_k(tr[root].size - k) + delta);}}printf("%d\n", tot - (tr[root].size - 2));return 0;
}
2. 树套树
2488. 树套树-简单版
- 题意:请你写出一种数据结构,来维护一个长度为 nnn 的序列,其中需要提供以下操作:
1 pos x,将 pospospos 位置的数修改为 xxx。2 l r x,查询整数 xxx 在区间 [l,r][l,r][l,r] 内的前驱(前驱定义为小于 xxx,且最大的数)。 - 线段树套 set.
#include<iostream>
#include<algorithm>
#include<cstring>
#include<set>
using namespace std;
const int maxn = 50010, maxm = maxn * 4, INF = 1e9;
int N, M;
struct Tree {int l, r;multiset<int> s;
}tr[maxm];
int w[maxn];
void build(int u, int l, int r) {tr[u] = { l, r };//加入两个哨兵tr[u].s.insert(-INF), tr[u].s.insert(INF);for (int i = l; i <= r; i++) {tr[u].s.insert(w[i]);}if (l == r) return;int mid = (l + r) / 2;build(2 * u, l, mid), build(2 * u + 1, mid + 1, r);
}
void change(int u, int pos, int x) {//这里一定要写成 find,不然会把所有 w[p] 删掉tr[u].s.erase(tr[u].s.find(w[pos]));tr[u].s.insert(x);if (tr[u].l == tr[u].r) return;int mid = (tr[u].l + tr[u].r) / 2;if (pos <= mid) change(u * 2, pos, x);else change(u * 2 + 1, pos, x);
}int query(int u, int l, int r, int x) {if (l <= tr[u].l && tr[u].r <= r) {auto it = tr[u].s.lower_bound(x);--it;return *it;}int mid = (tr[u].l + tr[u].r) / 2, res = -INF;if (l <= mid) res = max(res, query(2 * u, l, r, x));if (r > mid) res = max(res, query(2 * u + 1, l, r, x));return res;
}int main() {scanf("%d%d", &N, &M);for (int i = 1; i <= N; i++) scanf("%d", &w[i]);build(1, 1, N);while (M--) {int op;scanf("%d", &op);if (op == 1) {int pos, x;scanf("%d%d", &pos, &x);change(1, pos, x);w[pos] = x;}else {int l, r, x;scanf("%d%d%d", &l, &r, &x);printf("%d\n", query(1, l, r, x));}}return 0;
}
2476. 树套树
- 请你写出一种数据结构,来维护一个长度为 nnn 的数列,其中需要提供以下操作:
1 l r x,查询整数 xxx 在区间 [l,r][l,r][l,r] 内的排名。
2 l r k,查询区间 [l,r][l,r][l,r] 内排名为 kkk 的值。
3 pos x,将 pospospos 位置的数修改为 xxx。
4 l r x,查询整数 xxx 在区间 [l,r][l,r][l,r] 内的前驱(前驱定义为小于 xxx,且最大的数)。
5 l r x,查询整数 xxx 在区间 [l,r][l,r][l,r] 内的后继(后继定义为大于 xxx,且最小的数)。
- 线段树套splay(思路是比较简单的,看代码就行)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 1500010, INF = 1e9;
//50000 * 4 * 2 + n * logn 两个哨兵
int N, M;struct node {int s[2], p, v;int size;void init(int _v, int _p) {v = _v, p = _p;size = 1;}
}tr[maxn];// 为了防止变量名重复,这里的线段树用数组来表示
int L[maxn], R[maxn], T[maxn], idx;
int w[maxn];//平衡树部分
void pushup(int u) {tr[u].size = tr[tr[u].s[0]].size + tr[tr[u].s[1]].size + 1;
}void rotate(int x) {int y = tr[x].p, z = tr[y].p;int k = (tr[y].s[1] == x);tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;tr[x].s[k ^ 1] = y, tr[y].p = x;pushup(y), pushup(x);
}void splay(int& root, int x, int k) {while (tr[x].p != k) {int y = tr[x].p, z = tr[y].p;if (z != k) {if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);else rotate(y);}rotate(x);}if (!k) root = x;
}void insert(int& root, int v) {int u = root, p = 0;while (u) p = u, u = tr[u].s[v > tr[u].v];u = ++idx;if (p) tr[p].s[v > tr[p].v] = u;tr[u].init(v, p);splay(root, u, 0);
}
//返回以 T[u] 为根的小于等于 x 的数的个数
int get_k(int root, int v) {int u = root, res = 0;while (u) {if (tr[u].v < v) res += tr[tr[u].s[0]].size + 1, u = tr[u].s[1];else u = tr[u].s[0];}return res;
}
//把以 root 为根的splay,删掉x加上y
void update(int& root, int x, int y) {int u = root;while (u) {if (tr[u].v == x) break;else if (tr[u].v < x) u = tr[u].s[1];else u = tr[u].s[0];}splay(root, u, 0);//删掉平衡树的结点嘛,找到 u 的前驱和后继。int l = tr[u].s[0], r = tr[u].s[1];while (tr[l].s[1]) l = tr[l].s[1];while (tr[r].s[0]) r = tr[r].s[0];splay(root, l, 0), splay(root, r, l);tr[r].s[0] = 0;pushup(r), pushup(l);insert(root, y);
}//前驱
int get_pre(int root, int v) {int u = root, res = -INF;while (u) {if (tr[u].v < v) res = max(res, tr[u].v), u = tr[u].s[1];else u = tr[u].s[0];}return res;
}int get_suc(int root, int v) {int u = root, res = INF;while (u) {if (tr[u].v > v) res = min(res, tr[u].v), u = tr[u].s[0];else u = tr[u].s[1];}return res;
}// 线段树部分void build(int u, int l, int r) {L[u] = l, R[u] = r;insert(T[u], -INF), insert(T[u], INF);for (int i = l; i <= r; i++) insert(T[u], w[i]);if (l == r) return;int mid = (l + r) / 2;build(2 * u, l, mid), build(2 * u + 1, mid + 1, r);
}int query(int u, int a, int b, int x) {if (a <= L[u] && R[u] <= b) {//返回以 T[u] 为根的小于 x 的数的个数return get_k(T[u], x) - 1;}int mid = (L[u] + R[u]) / 2, res = 0;if (a <= mid) res += query(2 * u, a, b, x);if (b > mid) res += query(2 * u + 1, a, b, x);return res;
}void change(int u, int p, int x) {update(T[u], w[p], x);if (L[u] == R[u]) return;int mid = (L[u] + R[u]) / 2;if (p <= mid) change(2 * u, p, x);else change(2 * u + 1, p, x);
}int query_pre(int u, int a, int b, int x) {//找到以 T[u] 为根节点splay里面小于x的最大的数if (a <= L[u] && R[u] <= b) return get_pre(T[u], x);int mid = (L[u] + R[u]) / 2, res = -INF;if (a <= mid) res = max(res, query_pre(2 * u, a, b, x));if (b > mid) res = max(res, query_pre(2 * u + 1, a, b, x));return res;
}
int query_suc(int u, int a, int b, int x) {//找到以 T[u] 为根节点splay里面大于x的最小的数if (a <= L[u] && R[u] <= b) return get_suc(T[u], x);int mid = (L[u] + R[u]) / 2, res = INF;if (a <= mid) res = min(res, query_suc(2 * u, a, b, x));if (b > mid) res = min(res, query_suc(2 * u + 1, a, b, x));return res;
}int main() {scanf("%d%d", &N, &M);for (int i = 1; i <= N; i++) {scanf("%d", &w[i]);}build(1, 1, N);while (M--) {int op, a, b, x;scanf("%d", &op);if (op == 1) {//查询x的排名scanf("%d%d%d", &a, &b, &x);//query求的是小于 x 的个数printf("%d\n", query(1, a, b, x) + 1);}else if (op == 2) {//查询排名为 x 的值scanf("%d%d%d", &a, &b, &x);int l = 0, r = 1e8;while (l < r) {//最后让答案等于 r,所以向上取整int mid = (l + r + 1) / 2;if (query(1, a, b, mid) + 1 <= x) l = mid;else r = mid - 1;}printf("%d\n", r);}else if (op == 3) {//修改第pos的值为xscanf("%d%d", &a, &x);change(1, a, x);w[a] = x;}else if (op == 4) {//查询 x 的前驱scanf("%d%d%d", &a, &b, &x);printf("%d\n", query_pre(1, a, b, x));}else {//查询 x 的后继scanf("%d%d%d", &a, &b, &x);printf("%d\n", query_suc(1, a, b, x));}}return 0;
}
3. 分块
3.1 分块之基本思想
243. 一个简单的整数问题2
- 题意:给定一个长度为 NNN 的数列 AAA,以及 MMM 条指令,每条指令可能是以下两种之一:
C l r d,表示把 A[l],A[l+1],…,A[r]A[l],A[l+1],…,A[r]A[l],A[l+1],…,A[r] 都加上 ddd。Q l r,表示询问数列中第 l∼rl \sim rl∼r 个数的和。

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxn = 100010, maxm = 350;
typedef long long ll;
ll add[maxm], sum[maxm], w[maxn];
int N, M, len;int get(int i) {//看看映射到了哪一块儿,注意这种写法会让 1~i-1在第一段return i / len;
}void change(int l, int r, int d) {if (get(l) == get(r)) { //段内直接暴力for (int i = l; i <= r; i++) w[i] += d, sum[get(i)] += d;}else {int i = l, j = r;while (get(i) == get(l)) w[i] += d, sum[get(i)] += d, i++;while (get(j) == get(r)) w[j] += d, sum[get(j)] += d, j--;for (int k = get(i); k <= get(j); k++) {//这个地方,即使长度不足len也没有关系,因为询问的时候,这些长度不足len的段不会作为整体被询问到。sum[k] += len * d, add[k] += d;}}
}ll query(int l, int r) {ll res = 0;if (get(l) == get(r)) {for (int i = l; i <= r; i++) res += w[i] + add[get(i)];}else {int i = l, j = r;while (get(i) == get(l)) res += w[i] + add[get(i)], i++;while (get(j) == get(r)) res += w[j] + add[get(j)], j--;for (int k = get(i); k <= get(j); k++) res += sum[k];}return res;
}int main() {scanf("%d%d", &N, &M);len = sqrt(N);for (int i = 1; i <= N; i++) {scanf("%lld", &w[i]);sum[get(i)] += w[i];}char op[2];int l, r, d;while (M--) {scanf("%s%d%d", &op, &l, &r);if (op[0] == 'C') {scanf("%d", &d);change(l, r, d);}else printf("%lld\n", query(l, r));}return 0;
}
3.2 分块之块状链表
4. 莫队算法
- 序列大小为 nnn,询问次数为 mmm,询问维度为 ddd(比如普通莫队的维度为2,即 lll 和 rrr),那么相当于 mmm 个点均匀分布在维度为 ndn^dnd 的超立方体中,我们的目标就是找到一条哈密顿路,让路径总长度尽可能小一些. 为了方便起见,我们考虑在一个维度上面(ddd 个维度不过是乘了 d\sqrt dd),点的个数大概是 O(m1d)O(m^{\frac{1}{d}})O(md1) 个,因此在一个维度上面的相邻两点之间的距离为 nm1d\frac{n}{m^{\frac{1}{d}}}md1n. 哈密顿路径长度为 nmd−1dnm^{\frac{d-1}{d}}nmdd−1
- 就是我们要选择的块的大小 nm1d\frac{n}{m^{\frac{1}{d}}}md1n,整个算法的复杂度是 O(nmd−1d)O(nm^{\frac{d-1}{d}})O(nmdd−1)
4.1 莫队之基础莫队
- 据说奇数块儿升序,偶数块儿降序,这样子有些时候会快一些。
- 莫队算法开方的时候,千万别忘先强制类型转换为 doubledoubledouble,否则可能会整数溢出.
2492. HH的项链
-
给一个序列,给很多次询问,求某个区间不同数字的个数。
-
将 nnn 个数分成 n2m\sqrt{\frac{n^2}{m}}mn2 块。对所有询问进行排序,排序标准:
- $Q[i].left /len < Q[j].left / len $(块号优先排序)
- 如果1相同,则 Q[i].right<Q[j].rightQ[i].right < Q[j].rightQ[i].right<Q[j].right (按照查询的右边界排序)
- 关于 iii 和 jjj 到底怎么变化的问题,只需要记住,addaddadd 是下一个位置的数字,subsubsub 是上一个位置的数字.
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
int N, M, len;
const int maxn = 50010, maxm = 200010, maxs = 1000010;struct Query
{int id, l, r;
}q[maxm];
int w[maxn], cnt[maxs], ans[maxm];int get(int x)
{return x / len;
}bool cmp(const Query& a, const Query& b)
{int i = get(a.l), j = get(b.l);if (i != j) return i < j;return a.r < b.r;
}void add(int x, int& res)
{if (cnt[x] == 0) res++;cnt[x]++;
}
void del(int x, int& res)
{cnt[x]--;if (cnt[x] == 0) res--;
}int main() {scanf("%d", &N);for (int i = 1; i <= N; i++) scanf("%d", &w[i]);scanf("%d", &M);len = sqrt((double)N * N / (double)M);for (int i = 0; i < M; i++) {int l, r;scanf("%d%d", &l, &r);q[i] = { i, l, r };}sort(q, q + M, cmp);int res = 0;// i 指向前一个位置for (int k = 0, i = 0, j = 1; k < M; k++) {//这里 i 是右端点 j 是左端点int id = q[k].id, l = q[k].l, r = q[k].r;while (i < r) add(w[++i], res);while (i > r) del(w[i--], res);while (j < l) del(w[j++], res);while (j > l) add(w[--j], res);ans[id] = res;}for (int i = 0; i < M; i++) printf("%d\n", ans[i]);return 0;
}
树状数组做法
- 用树状数组维护。我们只关心右边的那个数字。比如 1 3 2 1,那么第一个 1 就不重要。我们就可以把第一个1减掉,把最后一个1加上。
- 具体思路是这样的,我们按照右端点对询问进行排序,然后让一个指针开始往右扫描,每次都记录每个颜色最后出现的位置,把那个位置的值置为1,假如这个颜色在之前出现过,就把那个位置置为0. 然后每次询问都查询 [l,r][l,r][l,r] 区间有多少个1. 这就是单点修改,区间查询问题,用树状数组维护.
#include<bits/stdc++.h>
using namespace std;
const int N = 50010, M = 200010;int tr[N], last[1000010], a[N], ans[M];
int n, m;struct P
{int l, r, id;bool operator < (const P& p) const{return r < p.r;}
}Q[M];int lowbit(int x)
{return x & -x;
}void add(int x, int c)
{for(int i = x; i <= n; i += lowbit(i)){tr[i] += c;}
}int sum(int x)
{int res = 0;for(int i = x; i; i -= lowbit(i)) res += tr[i];return res;
}int main()
{scanf("%d", &n);for(int i = 1; i <= n; i++){scanf("%d", &a[i]);}scanf("%d", &m);for(int i = 1; i <= m; i++){scanf("%d%d", &Q[i].l, &Q[i].r);Q[i].id = i;}sort(Q + 1, Q + m + 1);for(int i = 1, j = 1; i <= m; i++){for(; j <= Q[i].r; j++){if(last[a[j]]) add(last[a[j]], -1);add(j, 1), last[a[j]] = j;}ans[Q[i].id] = sum(Q[i].r) - sum(Q[i].l - 1);}for(int i = 1; i <= m; i++) printf("%d\n", ans[i]);return 0;
}4.2 莫队之带修改的莫队
2521. 数颜色
- 题意:墨墨购买了一套 NNN 支彩色画笔(其中有些颜色可能相同),摆成一排,你需要回答墨墨的提问。墨墨会像你发布如下指令:
Q L R代表询问你从第 LLL 支画笔到第 RRR 支画笔中共有几种不同颜色的画笔。R P Col把第 PPP 支画笔替换为颜色 ColColCol。 - 输入:1≤N,M≤100001\le N,M\le 100001≤N,M≤10000,修改操作不多于 100010001000 次,所有的输入数据中出现的所有整数均大于等于 111 且不超过 10610^6106。
- 设序列大小为 nnn,询问次数是 mmm,修改次数是 mmmt块的大小是 aaa,由于 mmm 中的 l,rl, rl,r 和 ttt 这三个询问的维度并不相等。因此分块大小应该这样计算:lll 移动次数为 O(am+n)O(am+n)O(am+n),rrr 移动次数是 O(am+n2a)O(am+\frac{n^2}{a})O(am+an2),ttt 的移动次数是 O(tn2a2)O(t\frac{n^2}{a^2})O(ta2n2). 然后接下来就是玄学推导。由于题目的 nnn 和 mmm 的范围大致一致,因此 lll 可以写为 O(an)O(an)O(an),rrr 可以写为 O(an)O(an)O(an),则由 an=tn2a2an = t\frac{n^2}{a^2}an=ta2n2 得 a=nt3a = \sqrt[3]{nt}a=3nt
- 其实就是排序的时候用到了分块儿,之后还是一个暴力做法。
#include<bits/stdc++.h>
using namespace std;
const int N = 10010, M = 1000010;int a[N], n, m, mc, mq, len;
int res, cnt[M], ans[N];struct Query
{int l, r, id, t;
}Q[N];struct Modify
{int p, c;
}c[N];int get(int x)
{return x / len;
}bool cmp(const Query& q1, const Query& q2)
{int l1 = get(q1.l), l2 = get(q2.l);int r1 = get(q1.r), r2 = get(q2.r);int t1 = q1.t, t2 = q2.t;if(l1 != l2) return l1 < l2;if(r1 != r2) return r1 < r2;return t1 < t2;
}void add(int x, int& res)
{if(cnt[x] == 0) res++;cnt[x]++;
}void sub(int x, int& res)
{cnt[x]--;if(cnt[x] == 0) res--;
}int main()
{scanf("%d%d", &n, &m);for(int i = 1; i <= n; i++){scanf("%d", &a[i]);}for(int i = 1; i <= m; i++){static char op[5];static int x, y;scanf("%s%d%d", op, &x, &y);if(*op == 'Q') mq++, Q[mq] = {x, y, mq, mc};else c[++mc] = {x, y};}int res = 0;len = cbrt(1.0 * n * (mc + 1));sort(Q + 1, Q + mq + 1, cmp);for(int k = 1, i = 1, j = 0, t = 0; k <= mq; k++){//这里的 i 表示左端点,j 表示右端点//一定要先改变右端点再改变左端点int l = Q[k].l, r = Q[k].r, id = Q[k].id, tm = Q[k].t;while(j > r) sub(a[j--], res);while(j < r) add(a[++j], res);while(i < l) sub(a[i++], res);while(i > l) add(a[--i], res);while(t < tm){t++;if(l <= c[t].p && c[t].p <= r){sub(a[c[t].p], res);add(c[t].c, res);}swap(a[c[t].p], c[t].c);}while(t > tm){if(l <= c[t].p && c[t].p <= r){sub(a[c[t].p], res);add(c[t].c, res);}swap(a[c[t].p], c[t].c);t--;}ans[id] = res;}for(int i = 1; i <= mq; i++){printf("%d\n", ans[i]);}return 0;
}
4.3 莫队之回滚莫队
有些题目在区间转移时,可能会出现增加或者删除无法实现的问题。在只有增加不可实现或者只有删除不可实现的时候,就可以使用回滚莫队在 O(nn)O(n \sqrt n)O(nn) 的时间内解决问题。回滚莫队的核心思想就是既然我只能实现一个操作,那么我就只使用一个操作,剩下的交给回滚解决。
回滚莫队分为只使用增加操作的回滚莫队和只使用删除操作的回滚莫队。以下仅介绍只使用增加操作的回滚莫队,只使用删除操作的回滚莫队和只使用增加操作的回滚莫队只在算法实现上有一点区别,故不再赘述。
2523. 历史研究
- 给一个序列 n≤105n \le 10^5n≤105,序列由一系列数字 Xi≤109X_i \le 10^9Xi≤109 组成,下面有一系列询问 m≤105m \le 10^5m≤105,每次询问一个区间 [l,r][l,r][l,r],求这个区间这个数的最大值:区间每个数出现次数 乘 这个数字.
- 这个题就是典型的增加方便删除困难,因为删除操作维护最大值不容易实现。这道题还有一个地方就是卡常,离散化用 vector 实现,更快一些.
- 首先分块排序,第一关键字按照左端点 lll 所在块升序排序,第二关键字按照右端点升序排序.
- 对于左右端点在同一块内的询问可以暴力处理
- 左右端点横跨两个块的询问(记为块 AAA 和 AAA 之外),初始时将右端点置于块 AAA 的右端点,左端点置于块 AAA 的右端点加 111 的位置,右端点只会一直往右左,暴力维护左端点即可。
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;typedef long long ll;
ll a[N], res, ans[N];
int len, idx;int cnt[N];
vector<ll> nums;int get_id(ll x)
{return lower_bound(nums.begin(), nums.end(), x) - nums.begin();
}struct Query
{int l, r, id;
}Q[N];void add(int x)
{cnt[x]++;if(cnt[x] * nums[x] > res) res = cnt[x] * nums[x];
}void sub(int x)
{cnt[x]--;
}int get(int x)
{return x / len;
}bool cmp(Query& q1, Query& q2)
{int l1 = get(q1.l), l2 = get(q2.l);if(l1 != l2) return l1 < l2;return q1.r < q2.r;
}int main()
{int n, m;scanf("%d%d", &n, &m);for(int i = 1; i <= n; i++){scanf("%lld", &a[i]);nums.push_back(a[i]);}sort(nums.begin(), nums.end());nums.erase(unique(nums.begin(), nums.end()), nums.end());//这样子,a中存储的就是每一个数字的相对大小了.for(int i = 1; i <= n; i++){a[i] = get_id(a[i]);}for(int i = 1; i <= m; i++){scanf("%d%d", &Q[i].l, &Q[i].r);Q[i].id = i;}len = sqrt(m);sort(Q + 1, Q + m + 1, cmp);for(int x = 1; x <= m; ){memset(cnt, 0, sizeof cnt);int y = x;while(y <= m && get(Q[x].l) == get(Q[y].l)) y++;while(x < y){res = 0;if(get(Q[x].l) != get(Q[x].r)) break;int l = Q[x].l, r = Q[x].r, id = Q[x].id;for(int k = l; k <= r; k++) add(a[k]);ans[id] = res;for(int k = l; k <= r; k++) sub(a[k]);x++;}int right = get(Q[x].l) * len + len - 1;int i = right + 1, j = right;res = 0;while(x < y){int l = Q[x].l, r = Q[x].r, id = Q[x].id;while(j < r) add(a[++j]);ll backup = res;while(i > l) add(a[--i]);ans[id] = res;res = backup;while(i < right + 1) sub(a[i++]);x++;}}for(int i = 1; i <= m; i++) printf("%lld\n", ans[i]);return 0;
}
4.4 莫队之树上莫队
2534. 树上计数2
- 给定一棵 N(N≤40000)N(N \le 40000)N(N≤40000) 个节点的树,节点编号从 111 到 NNN,每个节点都有一个整数权值。现在,我们要进行 M≤105M \le 10^5M≤105 次询问,格式为
u v,对于每个询问你需要回答从 uuu 到 vvv 的路径上(包括两端点)共有多少种不同的点权值。点的权值在 intintint 范围内.
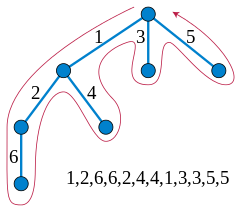
- 先把树的问题转化为序列问题,即求出树的欧拉序列.
- 记录每一个结点第一次出现的位置 first[u]first[u]first[u],和最后一次出现的位置 last[u]last[u]last[u].
- 不妨设 first[x]<first[y]first[x] < first[y]first[x]<first[y]:
- 若 lca(x,y)=xlca(x, y) = xlca(x,y)=x,则区间为在欧拉序列 [first[x],first[y]][first[x], first[y]][first[x],first[y]] 中只出现了一次的点.
- 若 lca(x,y)≠xlca(x, y) \ne xlca(x,y)=x,则区间为在欧拉序列 [last[x],first[y]][last[x], first[y]][last[x],first[y]] 中出现一次的点加上 lca(x,y)lca(x, y)lca(x,y).
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;int h[N], e[N], ne[N], idx;
int a[N], n, m, ans[N];
int seq[N], top, que[N], first[N], last[N];
vector<int> nums;int cnt[N], st[N];
int len;
int depth[N], f[N][16];void add_edge(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}struct Query
{int l, r, id, p;
}Q[N];int get(int x)
{return x / len;
}bool cmp(const Query& q1, const Query& q2)
{int l1 = get(q1.l), l2 = get(q2.l);if(l1 != l2) return l1 < l2;return q1.r < q2.r;
}void dfs(int u, int fa)
{seq[++top] = u;first[u] = top;for(int i = h[u]; i != -1; i = ne[i]){int v = e[i];if(v == fa) continue;dfs(v, u);}seq[++top] = u;last[u] = top;
}void bfs()
{memset(depth, 0x3f, sizeof depth);depth[0] = 0, depth[1] = 1;int hh = 0, tt = -1;que[++tt] = 1;while(hh <= tt){int u = que[hh++];for(int i = h[u]; i != -1; i = ne[i]){int v = e[i];if(depth[v] > depth[u] + 1){depth[v] = depth[u] + 1;f[v][0] = u;for(int k = 1; k <= 15; k++) f[v][k] = f[f[v][k - 1]][k - 1];que[++tt] = v;}}}
}int lca(int a, int b)
{if(depth[a] < depth[b]) swap(a, b);for(int k = 15; k >= 0; k--){if(depth[f[a][k]] >= depth[b]){a = f[a][k];}}if(a == b) return a;for(int k = 15; k >= 0; k--){if(f[a][k] != f[b][k]){a = f[a][k];b = f[b][k];}}return f[a][0];
}void add(int x, int& res)
{st[x] ^= 1;if(st[x]){cnt[a[x]]++;if(cnt[a[x]] == 1) res++;}else{cnt[a[x]]--;if(!cnt[a[x]]) res--;}
}int main()
{memset(h, -1, sizeof h);scanf("%d%d", &n, &m);for(int i = 1; i <= n; i++){scanf("%d", &a[i]);nums.push_back(a[i]);}sort(nums.begin(), nums.end());nums.erase(unique(nums.begin(), nums.end()), nums.end());for(int i = 1; i <= n; i++){a[i] = lower_bound(nums.begin(), nums.end(), a[i]) - nums.begin();}for(int i = 1; i < n; i++){int x, y;scanf("%d%d", &x, &y);add_edge(x, y), add_edge(y, x);}dfs(1, -1);bfs();for(int i = 1; i <= m; i++){int x, y;scanf("%d%d", &x, &y);if(first[x] > first[y]) swap(x, y);int p = lca(x, y);if(p == x) Q[i] = {first[x], first[y], i};else Q[i] = {last[x], first[y], i, p};}len = sqrt(top);sort(Q + 1, Q + m + 1, cmp);int res = 0;for(int i = 1, L = 1, R = 0; i <= m; i++){int l = Q[i].l, r = Q[i].r, id = Q[i].id, p = Q[i].p;while(R < r) add(seq[++R], res);while(R > r) add(seq[R--], res);while(L < l) add(seq[L++], res);while(L > l) add(seq[--L], res);if(p) add(p, res);ans[id] = res;if(p) add(p, res);}for(int i = 1; i <= m; i++){printf("%d\n", ans[i]);}
}
4.5 莫队之二次离线莫队
2535. 二次离线莫队
- 题意:给定一个长度为 nnn 的序列 a1,a2,...,ana_1,a_2,...,a_na1,a2,...,an 以及一个整数 kkk。现在要进行 mmm 次询问,每次询问给定一个区间 [l,r][l,r][l,r],请你求出共有多少个数对 (i,j)(i,j)(i,j) 满足 l≤i<j≤rl \le i < j \le rl≤i<j≤r 且 ai⊕aja_i \oplus a_jai⊕aj 的结果在二进制表示下恰好有 kkk 个 111。n≤105,0≤k≤14,0≤ai<214n\le 10^5,0\le k \le 14, 0 \le a_i < 2^{14}n≤105,0≤k≤14,0≤ai<214
5. 树链剖分
将树转化为一个序列,将树中路径转化为长度为 logn\log nlogn 段连续区间,也叫 logn\log nlogn 条重链.
基本概念
- 重儿子:父亲节点的所有儿子中子树结点数目最多(size最大)的结点;
- 轻儿子:父亲节点中除了重儿子以外的儿子;
- 重边:父亲结点和重儿子连成的边;
- 轻边:父亲节点和轻儿子连成的边;
- 重链:由多条重边连接而成的路径;
- 轻链:由多条轻边连接而成的路径;
性质
**对于节点数为 nnn 的树,从任意节点向上走到根节点,经过的轻边数量不会超过 logn\log nlogn. ** 这是因为当我们向下经过一条 轻边 时,所在子树的大小至少会除以二。所以说,对于树上的任意一条路径,把它拆分成从 lcalcalca 分别向两边往下走,分别最多走 O(logn)O(\log n)O(logn) 次,树上的每条路径都可以被拆分成不超过 O(logn)O(\log n)O(logn) 条重链。
对于每个轻儿子,如果该结点不是叶节点,那么他一定是重链的开始。
树上每个节点都属于且仅属于一条重链
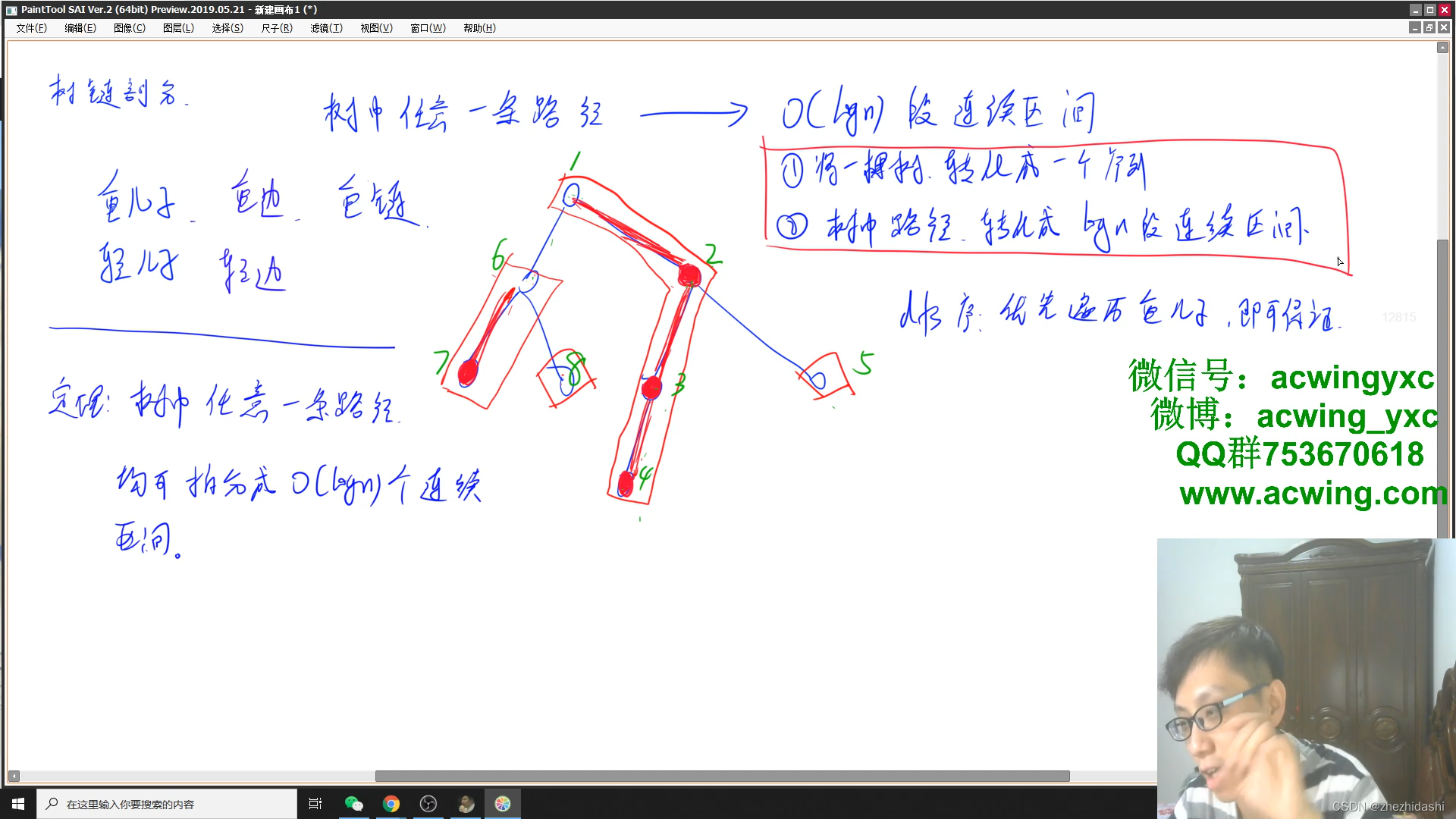
按照 DFSDFSDFS 序生成序列. 先访问重儿子,再访问轻儿子. 标红的点是重儿子,标红的边是重边.
一些定义
fa(x)fa(x)fa(x) 表示节点 xxx 在树上的父亲。
dep(x)dep(x)dep(x) 表示节点 xxx 在树上的深度。
sz(x)sz(x)sz(x) 表示节点 xxx 的子树的节点个数。
son(x)son(x)son(x) 表示节点 xxx 的 重儿子 ,即所有儿子中子树大小最大的一个。
定义 重边 表示连接两个重儿子的边。
定义 重路径 表示重边连成的一条链。
top(x)top(x)top(x) 表示节点 所在 重路径 的顶部节点(深度最小)。top(x)top(x)top(x) 一定是一个轻儿子。
id(x)id(x)id(x) 表示节点 xxx 的 时间戳 ,也是其在线段树中的编号。
nw(x)nw(x)nw(x) 表示时间戳为 xxx 的结点的权值。
我们进行两遍 DFS 预处理出这些值,其中第一次 DFS 求出 fa(x),dep(x),sz(x),son(x)fa(x),dep(x),sz(x),son(x)fa(x),dep(x),sz(x),son(x),第二次 DFS 求出 top(x),id(x)top(x),id(x)top(x),id(x)。
2568. 树链剖分
给定一棵树,树中包含 nnn 个节点(编号 1∼n1 \sim n1∼n),其中第 iii 个节点的权值为 aia_iai。初始时,111 号节点为树的根节点。现在要对该树进行 mmm 次操作,操作分为以下 444 种类型:
1 u v k,修改路径上节点权值,将节点 uuu 和节点 vvv 之间路径上的所有节点(包括这两个节点)的权值增加 kkk。
2 u k,修改子树上节点权值,将以节点 uuu 为根的子树上的所有节点的权值增加 kkk。
3 u v,询问路径,询问节点 uuu 和节点 vvv 之间路径上的所有节点(包括这两个节点)的权值和。
4 u,询问子树,询问以节点 uuu 为根的子树上的所有节点的权值和。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;const int N = 100010, M = N * 2;
int w[N], h[N], e[M], ne[M], idx;
int n, m;void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}int dep[N], sz[N], fa[N], son[N];
int nw[N], id[N], top[N], cnt;void dfs1(int u, int father, int depth)
{dep[u] = depth, sz[u] = 1, fa[u] = father;for(int i = h[u]; i != -1; i = ne[i]){int v = e[i];if(v == father) continue;dfs1(v, u, depth + 1);if(sz[son[u]] < sz[v]) son[u] = v;sz[u] += sz[v];}
}//t 表示当前结点所在重链的开头结点是什么
void dfs2(int u, int t)
{id[u] = ++cnt; nw[cnt] = w[u], top[u] = t;if(!son[u]) return;dfs2(son[u], t);for(int i = h[u]; i != -1; i = ne[i]){int v = e[i];//判断 v 是否为 father 时,千万别写错,不然可能会 MLEif(v == fa[u] || son[u] == v) continue;dfs2(v, v);}
}struct node
{int l, r;ll sum, add;
}tr[N * 4];void pushup(int u)
{tr[u].sum = tr[2 * u].sum + tr[2 * u + 1].sum;
}void pushdown(int u)
{auto& root = tr[u], &left = tr[2 * u], &right = tr[2 * u + 1];if(root.add){left.sum += root.add * (left.r - left.l + 1);right.sum += root.add * (right.r - right.l + 1);left.add += root.add, right.add += root.add;root.add = 0;}
}void build(int u, int l, int r)
{tr[u] = {l, r};if(l == r) tr[u].sum = nw[l];else{int mid = (l + r) / 2;build(2 * u, l, mid), build(2 * u + 1, mid + 1, r);pushup(u);}
}void update(int u, int l, int r, int k)
{if(l <= tr[u].l && tr[u].r <= r){tr[u].add += k;tr[u].sum += (ll)k * (tr[u].r - tr[u].l + 1);}else{pushdown(u);int mid = (tr[u].l + tr[u].r) / 2;if(l <= mid) update(2 * u, l, r, k);if(r > mid) update(2 * u + 1, l, r, k);pushup(u);}
}ll query(int u, int l, int r)
{if(l <= tr[u].l && tr[u].r <= r) return tr[u].sum;pushdown(u);int mid = (tr[u].l + tr[u].r) / 2;ll res = 0;if(l <= mid) res += query(2 * u, l, r);if(r > mid) res += query(2 * u + 1, l, r);return res;
}void update_path(int u, int v, int k)
{while(top[u] != top[v]){if(dep[top[u]] < dep[top[v]]) swap(u, v);//传进线段树的下标s结点编号。update(1, id[top[u]], id[u], k);u = fa[top[u]];}if(dep[u] < dep[v]) swap(u, v);update(1, id[v], id[u], k);
}void query_path(int u, int v)
{ll res = 0;while(top[u] != top[v]){if(dep[top[u]] < dep[top[v]]) swap(u, v);res += query(1, id[top[u]], id[u]);u = fa[top[u]];}if(dep[u] < dep[v]) swap(u, v);res += query(1, id[v], id[u]);printf("%lld\n", res);
}void update_tree(int u, int k)
{update(1, id[u], id[u] + sz[u] - 1, k);
}void query_tree(int u)
{printf("%lld\n", query(1, id[u], id[u] + sz[u] - 1));
}int main()
{scanf("%d", &n);for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);memset(h, -1, sizeof h);for (int i = 0; i < n - 1; i ++ ){int a, b;scanf("%d%d", &a, &b);add(a, b), add(b, a);}dfs1(1, -1, 1);dfs2(1, 1);build(1, 1, n);scanf("%d", &m);while (m -- ){int t, u, v, k;scanf("%d%d", &t, &u);if (t == 1){scanf("%d%d", &v, &k);update_path(u, v, k);}else if (t == 2){scanf("%d", &k);update_tree(u, k);}else if (t == 3){scanf("%d", &v);query_path(u, v);}else query_tree(u);}return 0;
}


![【论文阅读】[JBHI] VLTENet、[ISBI]](https://img-blog.csdnimg.cn/21f47ce9df0949a9bc686ce00d25bba0.png)
