基于PCA与LDA的数据降维实践

描述

数据降维（Dimension Reduction）是降低数据冗余、消除噪音数据的干扰、提取有效特征、提升模型的效率和准确性的有效途径， PCA（主成分分析）和LDA（线性判别分析）是机器学习和数据分析中两种常用的经典降维算法。

本任务通过两个降维案例熟悉PCA和LDA降维的原理、区别及调用方法。

源码下载

环境

操作系统：Windows 10、Ubuntu18.04
工具软件：Anaconda3 2019、Python3.7
硬件环境：无特殊要求

依赖库列表

matplotlib   	3.3.4
scikit-learn	0.24.2

分析

任务1、基于PCA算法实现鸢尾花数据集降维，涉及下列三个环节：

A）加载鸢尾花（Iris）数据并进行降维

B）降维后的数据可视化

C）使用K-NN算法进行分类，对比降维前后的分类准确性

任务2、基于LDA算法实现红酒数据集降维，涉及以下四个环节：

A）加载红酒数据集

B）使用PCA和LDA两种算法对数据进行降维

C）降维结果可视化

D）降维前后的分类准确性对比

实施

1、基于PCA算法实现鸢尾花数据集降维

鸢尾花数据原有四个特征维度，运用PCA算法将特征维度降为两个，之后进行可视化并运用K-NN算法进行分类，对比降维前后的分类准确性（数据降维的目的之一是提升模型的准确性）。

1.1 加载鸢尾花特征数据，并使用PCA算法降维

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier# 加载鸢尾花数据集
iris= load_iris()
data = iris.data # 特征数据
target = iris.target # 标签数据
print(data.shape) # 查看数据维度（150, 4）# PCA降维
pca = PCA(n_components = 2).fit(data) # 利用PCA算法降成2维
new_data = pca.transform(data)
print(new_data.shape) # 查看数据维度（150，2）

结果如下：

(150, 4)
(150, 2)

可以看到，鸢尾花数据由四维（四个特征）降为两维度。

1.2 数据可视化，并使用K-NN算法对比降维前后的分类准确性

# 降维后的数据集可视化
plt.title('Iris dimensions reduction: 4 to 2')
plt.scatter(new_data[:, 0], new_data[:, 1], c=target)
plt.show()# 使用KNN算法对比降维前后分类的准确性
model = KNeighborsClassifier(3)
score = model.fit(data, target).score(data, target)
print('4-dims:', score)
score = model.fit(new_data, target).score(new_data, target)
print('2-dims:', score)

输出结果：

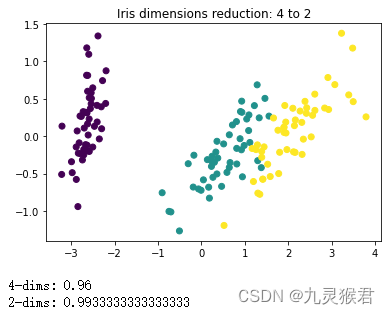
请添加图片描述

结果分析：

数据从4维降到2维后，可以很方便地进行可视化。从散点图中直观地看，降维后的数据较好地保留了原数据的分布信息。另外可以看到，降维后的KNN分类模型准确性有所提升，这也是数据降维的目的之一。

2、基于LDA算法实现红酒数据集降维

红酒数据集（Wine）有13个特征（即13个维度），我们分别使用PCA和LDA算法对数据集进行降维（降成2维），之后使用逻辑回归（LogisticRegression）分别在LDA算法降维前后的数据集上建立分类模型，对比同一种模型在数据集降维前后的准确性，直观感受数据降维对模型准确性的影响。

2.1 加载红酒数据集

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis 
from sklearn.datasets import load_wine# 加载红酒数据集
wine= load_wine()
data = wine.data
target = wine.target
print(data.shape) # 查看数据维度

2.2 分别使用LDA和PCA算法进行降维

# PCA降维（无类别）
pca = PCA(n_components = 2).fit(data) # 利用PCA算法降成2维
data_pca = pca.transform(data) # 降维转换
print('PCA:', data_pca.shape) # 查看数据维度# LDA降维（有类别，考虑样本标签）
lda = LinearDiscriminantAnalysis(n_components=2).fit(data, target)
data_lda = lda.transform(data)
print('LDA:', data_lda.shape)

结果如下：

(178, 13)
PCA: (178, 2)
LDA: (178, 2)

可以看到，两种算法都将红酒数据集由13维降成2维。

2.3 降维结果可视化

数据降到2维后，可以很方便地用散点图进行可视化，下面分别将两种算法降维后的红酒数据集进行可视化，对比其分布情况。

# LDA算法更适合有标签数据的降维
# 下面将两种方法降维后的数据进行可视化
fig = plt.figure(figsize=(12, 4)) # 生成画板# PCA降维结果
ax1 = fig.add_subplot(1, 2, 1) # 添加子图1
ax1.set_title('PCA')
ax1.scatter(data_pca[:, 0], data_pca[:, 1], c=target)# LDA降维结果
ax2 = fig.add_subplot(1, 2, 2) # 添加子图2
ax2.set_title('LDA')
ax2.scatter(data_lda[:, 0], data_lda[:, 1], c=target)plt.show() # 显示图像

显示结果：

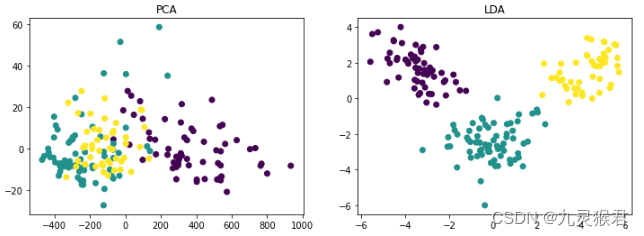
请添加图片描述

可以看到，LDA降维因为考虑到了样本的类别标签信息，降维后的数据分布能够较好地将类型分开。

2.4 LDA降维前后的分类准确性对比

使用逻辑回归算法，对LDA降维前后的数据集建立分类模型，对比其准确性。

from sklearn.model_selection import  train_test_split
from sklearn.linear_model import LogisticRegression# 1、使用逻辑回归模型，在降维前的数据集上训练并评估
X_train, X_test, y_train, y_test = train_test_split(data, target, random_state=0)model = LogisticRegression().fit(X_train, y_train)
score = model.score(X_test, y_test) # 在测试集上评估分类准确性
print(score)# 2、在LDA降维后的数据集上训练并评估
X_train, X_test, y_train, y_test = train_test_split(data_lda, target, random_state=0)
model = LogisticRegression().fit(X_train, y_train)
score = model.score(X_test, y_test) # 在测试集上评估分类准确性
print(score)