左神bilibili算法笔记-新手班

复杂度和简单算法

认识时间复杂度

常数时间的操作

一个操作如果和样本的数据量没有关系，每次都是固定时间内完成的操作，叫做常数操作。

时间复杂度为一个算法流程中，常数操作数量的一个指标。常用0(读作big 0)来表示。具体
来说，先要对一个算法流程非常熟悉，然后去写出这个算法流程中，发生了多少常数操作,
进而总结出常数操作数量的表达式。

在表达式中，只要高阶项，不要低阶项，也不要高阶项的系数，剩下的部分如果为f(N)，那.
么时间复杂度为0(f (N))。

评价一个算法流程的好坏，先看时间复杂度的指标，然后再分析不同数据样本下的实际运行
时间，也就是“常数项时间”。

选择排序

动图演示：

选择排序是一种简单直观的排序算法，其基本原理是每一次从待排序的数组里找到最小值（最大值）的下标，然后将最小值（最大值）跟待排序数组的第一个进行交换，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。反复的进行这样的过程直到待排序的数组全部有序。

代码实现：

public class SelectSort {public void selectionSort(int[] arr) {//考虑特殊（长度为0或1不用做）if (arr == null || arr.length < 2) {return;}for (int i = 0; i < arr.length - 1; i++) {int minNum = i;for (int j = i + 1; j < arr.length; j++) {//从头遍历，获取排序后数组某位置最小值minIndex = arr[j] < arr[minIndex] ? j : minIndex;}//交换某位置最小值与原位置值。swap(arr, minNum, i);}}public void swap(int[] arr, int src, int dest) {int temp = arr[src];arr[src] = arr[dest];arr[dest] = temp;}
}

看：N + N-1 + N-2 + N-3 + ....

比：N + N-1 + N-2 + ....

swap：N次

等差数列：aN^2 + bN + c

既时间复杂度O(n^2)，空间复杂度O(1)

冒泡排序

动图演示：

每一趟只能确定将一个数归位。即第一趟只能确定将末位上的数归位，第二趟只能将倒数第 2 位上的数归位，依次类推下去。如果有 n 个数进行排序，只需将 n-1 个数归位，也就是要进行 n-1 趟操作。

而 “每一趟 ” 都需要从第一位开始进行相邻的两个数的比较，将较大的数放后面，比较完毕之后向后挪一位继续比较下面两个相邻的两个数大小关系，重复此步骤，直到最后一个还没归位的数。

代码实现：

public class BubbleSort {public void bubbleSort(int[] arr) {if (arr == null || arr.length < 2) {return;}for (int i = 0; i < arr.length - 1; i++) {for (int j = 0; j < arr.length - 1 - i; j++) {if (arr[j] > arr[j + 1]) {swap(arr, j, j + 1);}}}}public void swap(int[] arr, int src, int dest) {arr[src] = arr[src] ^ arr[dest]; arr[dest] = arr[src] ^ arr[dest]; arr[src] = arr[src] ^ arr[dest];}
}

异或操作

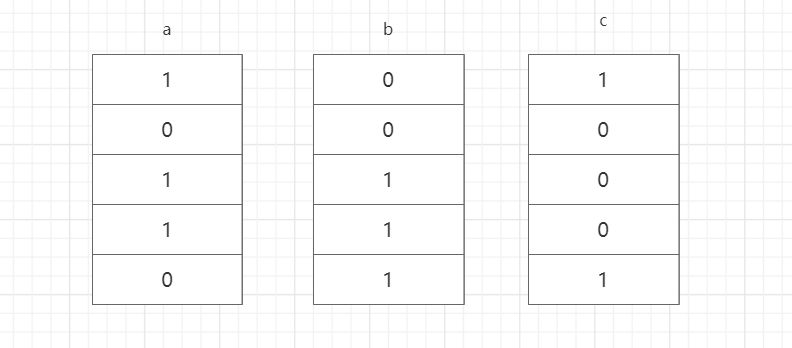
满足交换律 a ^ b = b ^ a

满足结合律 a ^ (b ^ c) = (a ^ b) ^ c

相当于无进位相加

某一位上的最终数值，与该位运算顺序无关，与0或1的出现次数有关

public void swap(int[] arr, int src, int dest) {int temp = arr[src];arr[src] = arr[dest];arr[dest] = temp;
}//此交换方式与上面相比，不用多开辟一个变量空间
public void swap(int[] arr, int src, int dest) {arr[src] = arr[src] ^ arr[dest]; arr[dest] = arr[src] ^ arr[dest]; arr[src] = arr[src] ^ arr[dest];
}

证明上式：

a = 甲；b = 已；

a = a ^ b; a = 甲 ^ 已

b = a ^ b； b = 甲 ^ 已 ^ 甲 = 已

a = a ^ b； a = 甲 ^ 已 ^ 已 = 甲

关于异或的两个问题

一组数只有一个数出现一次，其他出现两次，找出这个出现一次的数

解题思路：两个相同的数异或的结果为0，所以所有数异或之后，剩下的是0异或那个剩下的出现一次的数，无论什么数异或0都是自身

代码实现：

public void process(int[] arr) {int result = 0;for (int i = 0; i < arr.length; i++) {result ^= arr[i];}System.out.println(result);
}

一组数只有两个数出现一次，其他出现两次，找出这两个数

解题思路：全部数异或，得到a^{b且a!=b，故a}b一定有一位异或不为0。假设a^b在某一位上不同，则说明a或b在这一位上不同，因为其他偶数次的不管是0还是1，异或起来都为0了。故若只取在这一位上为1的数去进行异或，得到的数一定是a或者b。

代码实现：

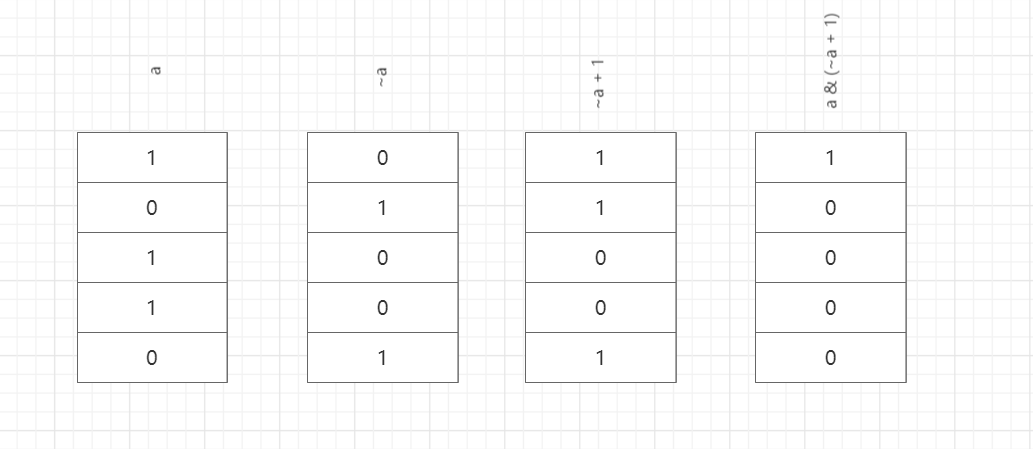
public void process(int[] arr) {int result = 0;for (int i = 0; i < arr.length; i++) {result ^= arr[i];}//二进制位上的位次最右第一个1的位置int rightOne = result & (~result + 1);int result2 = 0;for (int i = 0; i < arr.length; i++) {// 对应位为1的值取出进行^最后的到两个单数对应位为1的// 这里应该是(cur & rightOne) == rightOne或0， 0与任何数与都是0，故可判断在该位上是否为1if ((arr[i] & rightOne) == rightOne) {result2 ^= arr[i];}}System.out.println(result2 + "<=>" + (result ^ result2));}
}

取某数最右侧a & (~a + 1)

插入排序

动图演示：

从数组开头往后遍历，每次保证0到i子序列有序，方法为将i位置的数与0到i-1位置的已有序的子序列的每一个元素（从下标大的数开始）比较大小，插入使0到i子序列有序的位置即可。

该算法与选择排序和冒泡排序不同的点在于，其复杂度与数据分布有关，因为插入即停，故比对总次数与原序列的顺序情况有关。

时间复杂度是按照最差表现估计的。故插入排序的时间复杂度也是O(n^2)

代码实现：

public class InsertSort {public void insertSort(int[] arr) {if (arr == null || arr.length < 2) {return;}for (int i = 1; i < arr.length; i++) {for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {swap(arr, j, j + 1);}}}public void swap(int[] arr, int src, int dest) {int temp = arr[src];arr[src] = arr[dest];arr[dest] = temp;}
}

二分查找

为防止溢出，可用位运算右移一位即为除二向下取整（可用多项式表示推导）的方式求俩数的平均。

mid = ((R - L) >> 1) + L

下面会发现有mid = (R + L + 1)/ 2的情况，是因为查找边界数的时候会出现发现大于/小于的数时会暂时保留这个数，那就会出现if (nums[mid] == target) left = mid;这样的情况，不加1会导致无限循环下去

有序数组判断数存在

每次对比后可砍掉一半数据，时间复杂度为O(logN)

经典二分查找代码实现：

public int binarySearch(int[] arr, int num) {int left = 0;int right = arr.length - 1;while (left <= right) {int mid = ((right - left) >> 1) + left;if (arr[mid] == num) {return mid;} else if (arr[mid] < num) {left = mid + 1;} else {right = mid - 1;}}return -1;
}

有序数组找边界数

查找大于该值的最小值

例如找大于7的最小值

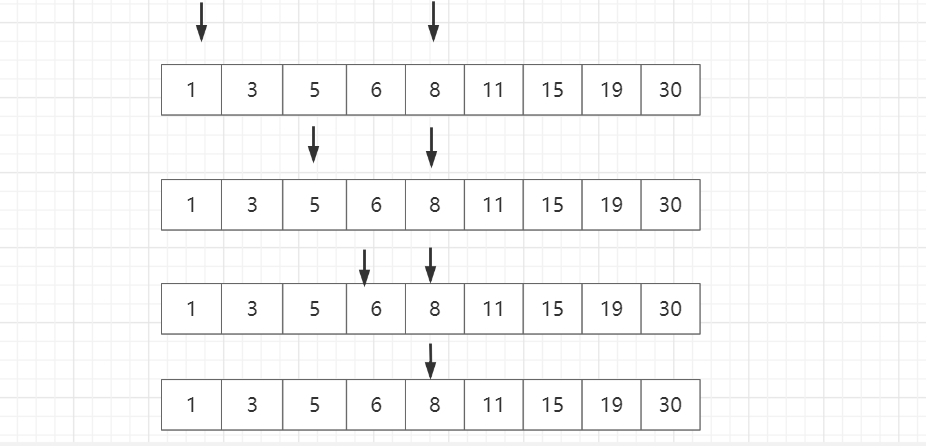
代码实现：

public class Main {public static int binarySearch(int[] arr, int L, int R, int value) {while (L < R) {int med = ((R - L) >> 1) + L;if (arr[med] == value) {return med;} else if (arr[med] < value) {L = med + 1;} else {R = med;}}return L;}
}

下面题目跟上面一题思想一致，注意指针边界即可

查找小于该值的最大值

代码实现：

public class Main {public static int binarySearch(int[] arr, int L, int R, int value) {while (L < R) {int med = ((R - L + 1) >> 1) + L;if (arr[med] == value) {return med;} else if (arr[med] < value) {L = med;} else {R = med - 1;}}return L;}
}

查找大于等于目标值的最右值

代码实现：

public class Main {// 返回大于等于target的最右元素private int rightest(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left < right) {int mid = (left + right + 1) / 2;if (nums[mid] == target) left = mid;else if (nums[mid] < target) left = mid + 1;else right = mid - 1;}return left;}
}

查找小于等于目标值的最左值

代码实现：

class Main {// 返回小于等于target最左元素private int leftest(int[] nums, int target) {int left = 0, right = nums.length - 1;while (left < right) {int mid = (left + right) / 2;if (nums[mid] == target) right = mid;else if (nums[mid] < target) left = mid + 1;else right = mid - 1;}return left;}
}

查找极小值

题目：极值定义该值比左右的值都小，如果是在数组两侧则只比较一点即可。

在无序数组中找到该极小值。

解题思路：先判断0位置是不是局部最小，再判断N位置是不是局部最小，若都不是，则局部最小必在0到N之间，取中点M，若其不为局部最小，则必在某向下方向位置有局部最小，继续二分，直到找到

因为值比左右的值都小，所有必定存在类似图中数字55的转折点

代码实现：

public class Main {public Integer process(int[] arr) {//判断数组是否为空if (arr == null || arr.length == 0) {return null;}//只有一个数组直接返回即可if (arr.length == 1) {return arr[0];}//第一个数字就已经符合if (arr[0] < arr[1]) {return arr[0];}//最后一个数组就已经符合if (arr[arr.length - 1] < arr[arr.length - 2]) {return arr[arr.length - 1];}//二分查找int l = 0;int r = arr.length - 1;while (l < r) {int mid = ((r - l) >> 1) + l;if (arr[mid] < arr[mid + 1]) {r = mid;}else {l = mid + 1;}}return arr[l];}
}

对数器

对数器的概念和使用

有一个你想要测的方法a
实现复杂度不好但是容易实现的方法b
实现一个随机样本产生器
把方法a和方法b跑相同的随机样本，看看得到的结果是否一样。
如果有一个随机样本使得比对结果不-致，打印样本进行人工干预，改对方法a或者
方法b
当样本数量很多时比对测试依然正确，可以确定方法a已经正确。

认识O(NlogN)排序

递归行为与其时间复杂度

剖析递归行为和递归行为时间复杂度的估算
用递归方法找一个数组中的最大值，系统上到底是怎么做的?

代码实现：

public class Main {public int process(int[] arr, int start, int end) {if (start == end) {return arr[start];}int mid = (start + end) / 2;int left = process(arr, start, mid); //N/2int right = process(arr, mid + 1, end); //N/2return Math.max(left, right);// O(1)}
}
//T(N) = 2T(N/2) + O(1)
//logb^a > d =>  复杂度为0(N^log(b, a)) = O(N^1)

master公式的使用
T(N) = a*T(N/b) + 0(N^d)

log(b,a) > d ->复杂度为0(N^log(b, a))
log(b,a) = d ->复杂度为0(N^d * logN)
log(b,a) < d ->复杂度为0(N^d)
补充阅读:[www. gocalf. com/blog/aIgorithmcomplexity-and-master-theorem. html](www. gocalf. com/blog/aIgorithmcomplexity-and-master-theorem. html)

归并排序

该方法思想在于：可将数组排序问题拆分为自相型的子问题，即拆分成左右子序列局部各自有序后进行双指针的归并排序。该子问题归并排序可通过

依次修改原数组在指定位置的值；
开辟新的内存空间替换原数组实现。本质上是利用左右子序列排好序后可进行双指针排序（O(n)）进行全局排序。

代码实现：

public class MergeSort {@Testpublic void test() {}public void process(int[] arr, int l, int r) {int mid = ((r - l) >> 1) + l;process(arr, l, mid);process(arr, mid + 1, r);merger(arr, l, mid, r);}private void merger(int[] arr, int l, int mid, int r) {int[] temp = new int[r - l + 1];int i = 0;int p1 = l;int p2 = mid + 1;while (p1 <= mid && p2 <= r) {temp[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];}while (p1 <= mid) {temp[i++] = arr[p1++];}while (p2 <= r) {temp[i++] = arr[p2++];}for (int j = 0; j < temp.length; j++) {arr[l + j] = temp[j];}}
}

时间复杂度计算：

process(arr, l, mid); N/2
process(arr, mid + 1, r); N/2
merger(arr, l, mid, r); o(N)

T(N) = 2T(N/2) + O(N)

log(b,a) = d => N*(logN)

复杂度较前几个排序方法更低的原因在于：

减少了无效的比较行为,每次merger小排序都会为后面的排序起到作用

时间复杂度O(n * logn) 空间复杂度 O(n)

归并排序的拓展（求小和）

小和问题

题目：每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。
例子:[1,3,4,2,5] 1左边比1小的数，没有; 3左边比3小的数，1; 4左
边比4小的数，1，3; 2左边比2小的数，1; 5左边比5小的数，1、3、4
2;所以小和为1+1+3+1+1+3+4+2=16
逆序对问题在一个数组中，左边的数如果比右边的数大，则折两个数
构成一个逆序对，请打印所有逆序对。

解题思路：

之前有个疑惑，为什么要排序之后再看有多少比当前数大的，其实排序就是为了减少比较行为，因为我一旦知道右边部分第一个数比当前数大之后就可以根据右边数据的多少决定当前数应该出现的次数

public class MinimalSum {int res;@Testpublic void test() {int[] arr = new int[]{1, 3, 4, 2, 5};process(arr, 0, arr.length - 1);System.out.println(res);}public void process(int[] arr, int l, int r) {if (l == r) {return;}int mid = (l + r) / 2;process(arr, l, mid);process(arr, mid + 1, r);merger(arr, l, mid, r);}private void merger(int[] arr, int l, int mid, int r) {int[] temp = new int[r - l + 1];int i = 0;int p1 = l;int p2 = mid + 1;while (p1 <= mid && p2 <= r) {res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;temp[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];}while (p1 <= mid) {temp[i++] = arr[p1++];}while (p2 <= r) {temp[i++] = arr[p2++];}for (int j = 0; j < temp.length; j++) {arr[l + j] = temp[j];}}
}

逆序对

题目：数组中的两个数，若前面的一个数大于后面的一个数，那么这两个数组成一个逆序对。输入一个数组，返回逆序对的个数。

解题思路：本质和求小和一样，归并过程中当左子序列的数比右子序列数大时，输出该逆序对即可。因为有序，复杂度也不高。

代码参考上面小和

对于这三个问题的总结与思考：

其实本质上就是将问题分解为左右两个有序子序列的对应问题，因为有序所以两个子序列中两个数，若满足一定大小关系，则可说明其他数也满足这个关系，就不需要再比较了。举例说明，当左右两个子序列都是按从小到大排序时，此时若左子序列的某个数大于右子序列某数，则可称左子序列往右所有数都大于右子序该数，即此数是全局最小，包含右子序列的该数的逆序对个数叠加后，即可进入空数组不用参与计算了。

核心就在于将左右有序子序列的两个数的大小关系转换为了全局最小（最大）。那么无论是排序，还是求小和，还是求逆序对，因为全局最小的缘故，都不会有大小关系比对的遗漏或者重复。

荷兰国旗问题

问题一
给定一个数组arr，和一个数num，请把小于等于num的数放在数组的左边，大于num的
数放在数组的右边。要求额外空间复杂度0(1)，时间复杂度0 (N)
问题二(荷兰国旗问题)
给定一个数组arr，和一个数num，请把小于num的数放在数组的左边，等于num的数放
在数组的中间，大于num的数放在数组的右边。要求额外空间复杂度0(1)，时间复杂度
0(N)

问题一解题思路：

快慢指针，快指针拿来遍历左区域外的数。若快指针所指数满足小于num，则与左区域外的第一个数交换，慢指针右移一位；若不小于，则啥也不做，快指针右移。
设置两个指针，一个从数组左边开始遍历，一个从数组右边开始遍历。当左与右都大于num时，右满足，左不满足，此时右指针向左移动，直到找到比num小的数，与左指针所指的数交换，交换完后，左右指针同时移动一格；若都小于等于，则对称的做；若一大一小，视情况交换，直到左右指针相遇。

问题二解题思路：再加两个中间指针，从数组中点向左或右移动，与问题一类似。但是遇到某一端值等于num则要与这个指针对应数做交换，左中间指针数与左指针数交换，右中间指针数与右指针数交换，当有一端相遇，剩下那端也要与右中间指针交互。

问题一快慢指针

public int partition(int[] arr, int L, int R) {int less = L;int num = arr[R];while (L < R) {if (arr[L] <= num) {swap(arr, less++, L++);} else {L++;}}swap(arr, less, L);return less;
}

荷兰国旗问题：以arr[R]做划分值，返回数组中等于arr[R]的下标范围。(指的就是partition划分的过程)

public static int[] netherlandsFlag(int[] arr, int L, int R) {if (L > R) {return new int[]{-1, -1};}if (L == R) {return new int[]{L, R};int less = L - 1;int more = R;int index = L;while (index < more) {Iif (arr[index] == arr[R]) {index++;} else if (arr[index] < arr[R]) {swap(arr, index++, ++less);} else {swap(arr, index, --more);}}swap(arr, more, R);return new int[]{less + 1, more};}
}

快排

快排1.0的实现：以arr[R]为划分值，每次与划分值相等的将会放在左边。O(N^2^)

public static void quickSort1(int[] arr) {if (arr == nu11|l arr .length < 2) {return;}process1(arr, 0, arr .1ength - 1);
}
public static void process1(int[] arr, int L，int R) {if(L>=R){return;}int M = partition(arr, L, R);process1(arr, L, M - 1);process1(arr, M + 1, R);
}

快排2.0的实现(以arr[R]作为划分值)：一次将相等的一批数放在中间，基于荷兰国旗问题。O(N^2^)

public static void quickSort2(int[] arr) {if (arr == nu11|l arr .length < 2) {return;}process1(arr, 0, arr.length - 1);
}
public static void process2(int[] arr, int L，int R) {if(L>=R){return;}int[] equalArea= netherlandsFlag(arr, L, R);process1(arr, L, equalArea[0] - 1);process1(arr, equalArea[1] + 1, R);
}

快排3.0的实现：随机选一个数作为划分值(涉及数学概念问题)，以及加上荷兰国旗问题的优化，复杂度为O(NlogN)

public static void quickSort3(int[] arr) {if (arr == nu11|l arr .length < 2) {return;process1(arr, 0, arr .1ength - 1);
}
public static void process3(int[] arr, int L，int R) {if(L>=R){return;}swap(arr,L + (int)(Math.random() * (R - L + 1)) , R);int equalArea= netherlandsFlag(arr, L, R);process1(arr, L, equalArea[0] - 1);process1(arr, equalArea[1] + 1, R);
}

下面是常见的快排方式

双指针快排代码实现：

public class QuickSort {private static void quickSort(int[] arr, int start, int end) {if (start < end) {//作为基准int part = start + (int) (Math.random() * (end - start + 1));int left = start;int right = end;while (left < right) {//右边数大while (left < right && part <= arr[right]) {right--;}arr[left] = arr[right];//左边数大while (left < right && part >= arr[left]) {left++;}arr[right] = arr[left];}arr[left] = part;//处理左边数据quickSort(arr, start, left);//处理右边数据quickSort(arr, left + 1, end);}}
}

堆及排序总结

堆

基本概念

堆在逻辑概念上是完全二叉树。

完全二叉树：设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，

第 h 层所有的结点都连续集中在最左边

满二叉树：深度为k且有2^k-1个结点的二叉树称为满二叉树

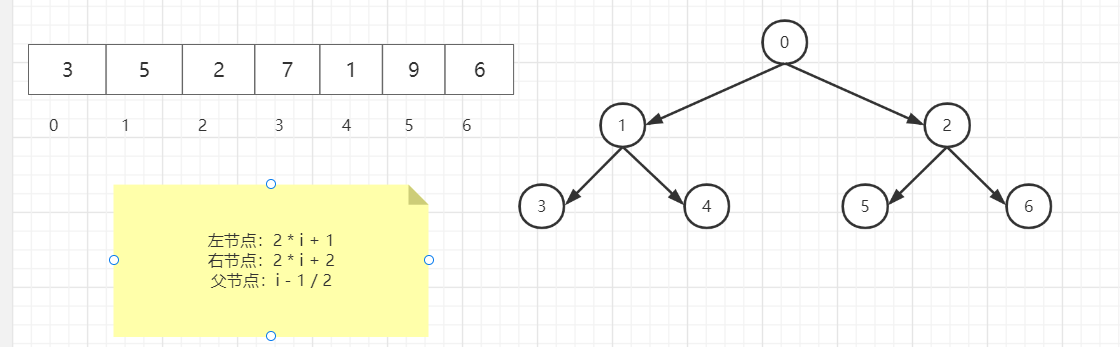
将数组从左到右放入完全二叉树中(用数组实现的完全二叉树叫堆)，可以得到以下规律：已知数组中一个下标 i ，可求解左child，右child及其父的下标。

堆是一种特殊的完全二叉树，堆分为大根堆（max-Heap）和小根堆(min-Heap)。

max-heap: 父节点的值比每一个子节点的值都要大

min-heap: 父节点的值比每一个子节点的值都要小

这个堆属性对任意层级的子树都成立（即任意层级的子树的根一定是最大或最小的）。这个属性很重要，在堆的插入和弹出时，依赖这个属性来保证新的堆的堆属性与原堆一致。

根据这一属性，那么最大堆总是将其中的最大值存放在树的根节点。而对于最小堆，根节点中的元素总是树中的最小值。堆属性非常有用，因为堆常常被当做优先队列使用，因为可以快速地访问到“最重要”的元素。

注意：堆的根节点中存放的是最大或者最小元素，但是其他节点的排序顺序是未知的。例如，在一个最大堆中，最大的那一个元素总是位于 index 0 的位置，但是最小的元素则未必是最后一个元素。唯一能够保证的是最小的元素是一个叶节点，但是不确定是哪一个。

堆的heapInsert

以最大堆为例，遍历原数组，按照完全二叉树的生成规则，满足一定的父子关系，可知当前节点的父节点下标，与父节点比较，更大则交换，重复这个过程比较该元素与所在节点的父节点元素的大小，直到上浮到不能上浮，则插入新的元素。遍历完成整个数组，则该数组实现了一个最大堆。

从代码实现上说，上浮过程只需要传入数组与需要heapInsert的元素下标即可实现。

代码实现：

 public void heapify(int[] arr, int index) {while (arr[index] > arr[(index - 1) / 2]) {swap(arr, index, (index - 1) / 2);index = (index - 1) / 2;}}

堆的heapify

以最大堆为例，当需要弹出根节点（即求数组最大或最小时），仍需要保证剩余数组满足堆属性。方法为：

将树的最右叶节点（删除后仍满足完全二叉树）放入需要heapify的根节点上。
将根节点数与根节点左右child进行大小比较，若有大于根节点数的子，将左右子的最大者与根节点数交换(因为堆属性，故根节点的两个子一定是各自子树的最大，与两子更大者交换后就是全局最大)，继续下沉过程，直到这个数不能下沉，即没有更大的子（1. 无子 2.有子但不大于根）。

从代码实现上说，下沉操作需要知道当前的堆的界，以此来判断是否还有左右子来进行循环终止。

代码实现：

public void heapify(int[] arr, int index, int heapSize) {//左孩子坐标int left = index * 2 + 1;//下方还有孩子时进入循环while (left < heapSize) {//选取左孩子和右孩子中较大的一个int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;if (arr[largest] > arr[index]) {swap(arr, largest, index);index = largest;left = index * 2 + 1;}}}

上面两个操作的复杂度与堆的高度有关，有N = 2 ^ (H - 1)，故H = logN。所以复杂度是logN

堆排序

其实就是对数组进行一次最大堆改造（交换数组内元素的位置，即对元素中的每一个数heapInsert）。然后将根（此时数组的index=0）处的数与数组最后一个元素交换，后续对除了这个最大值的数组（不考虑数组这个下标了）再进行最大堆操作（即对根进行heapify操作）以保证最大堆属性。重复该过程，直到没有元素需要heapify。

本质就是不断进行最大堆操作的同时，对已知的最大不再进行处理。

整个代码的实现过程中，不需要额外开辟数组空间，需要一直记录满足最大堆的下标上界即可。需要两个函数，一个heapInsert函数用来做上浮，一个heapify函数用来做下沉即可。上浮与下沉函数都是只做数组元素的交换。

代码实现：

    public void heapSort(int[] arr, int index) {if (arr == null || arr.length < 2) {return;}for (int i = 0; i < arr.length; i++) {heapInsert(arr, i);}int heapSize = arr.length;swap(arr, 0, --heapSize);while (heapSize > 0) {heapify(arr, 0, heapSize);swap(arr, 0, --heapSize);}}

从代码分析可知，时间复杂度是O(n * logn)，额外空间复杂度是O(1)。

构造最大堆的过程可优化，可不用上浮的方式，改为所有层级子树的根进行下浮，因为下浮的层级是从小到大的，所以可以降低复杂度。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FxnyzMMn-1670957410668)(https://work-qgs.oss-cn-shenzhen.aliyuncs.com/typora/image-20220830004640261.png)]

数组后面往前遍历，当遍历到7节点时，因为7节点有子节点，会进行heapify把已7为根的子数调整成大根堆，后面步骤类似

代码实现：

    public void heapSort(int[] arr, int index) {if (arr == null || arr.length < 2) {return;}for (int i = arr.length - 1; i >= 0; i--) {heapify(arr, i, arr.length);}int heapSize = arr.length;swap(arr, 0, --heapSize);while (heapSize > 0) {heapify(arr, 0, heapSize);swap(arr, 0, --heapSize);}}

堆对应练习

堆排序的地位远远没有堆结构重要！！！

题目一：
已知一个几乎有序的数组，几乎有序是指，如果把数组排好顺序的话，每个元素移动的距离可以不超过k,并且k相对于数组来说比较小。请选择一个合适的排序算法针对这个数据进行排序。

解题思路：说明接近堆结构，且如果是排序好的数组每个位置真实的值必在与原数组距离在K内。例如最后在0位置的数必在原来的0到6的下标范围内。故可以对该局部进行最小堆排序，求其最小值。依次遍历下去。

代码实现：

public class Main {public void sortedArrDistanceLessK(int[] arr, int k) {PriorityQueue<Integer> heap = new PriorityQueue<>();int index = 0;for (; index <= Math.min(arr.length, k); index++) {heap.add(arr[index]);}int i = 0;for (; index < arr.length; index++, i++) {heap.add(arr[index]);arr[i] = heap.poll();}while (!heap.isEmpty()) {arr[i++] = heap.poll();}}
}

各语言的堆结构虽然方便，但是不能完全满足需求。例如想要调整已经加入堆中的数据，这个需要自己手写一个堆

计数排序

动图演示：

之前所有排序都是基于比较的排序，计数排序是不基于比较的排序。

不基于比较的排序都是基于数据状况的排序，没有基于比较的排序应用范围广。

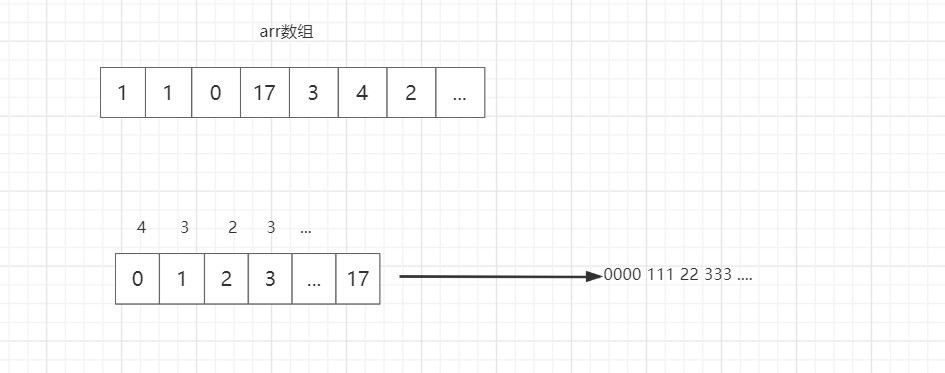
创建额外等长有序的数组空间，遍历原数组，给新数组每个下标对应元素计数，最后根据计数平铺即可实现排序。

基数排序

动图演示：

以十进制数的从小到大排序为例：

创建十个队列代表0到9，按数字位数从个位数开始入队列，然后出队列（出队列的顺序是，按队列序号从小到大出，队列中则是先进先出。这样做的原因是，队列间都是同位数比较，大的在后；队列内部则保持入队前的数的顺序）。做完全部位数即完成了排序。

代码实现：

public class RadixSort {public void radixSort(int[] arr) {if (arr == null || arr.length < 2) {return;}int max = maxBits(arr);int[][] bucket = new int[10][arr.length];int[] bucketElementCount = new int[10];for (int i = 0, n = 1; i < max; i++, n *= 10) {for (int j = 0; j < arr.length; j++) {int value = arr[j] / n % 10;bucket[value][bucketElementCount[value]++] = arr[j];}int index = 0;for (int k = 0; k < bucketElementCount.length; k++) {if (bucketElementCount[k] != 0) {for (int j = 0; j < bucketElementCount[k]; j++) {arr[index++] = bucket[k][j];}}bucketElementCount[k] = 0;}}}private int maxBits(int[] arr) {int maxNum = Integer.MIN_VALUE;for (int i = 0; i < arr.length; i++) {maxNum = Math.max(arr[i], maxNum);}int res = 0;while (maxNum != 0) {maxNum /= 10;res++;}return res;}
}

可以采取计数后计算前缀和的方式，计数得到按该位数排序后原来数组的某个数在新数组的位置（个位数为几的第几个出现），因为每次都是先进先出，故从数组末尾往前遍历模拟先进先出，此时可以在新数组上实现该位数的排序。重复这个过程

代码实现：

public class RadixSort {public void radixSort(int[] arr) {if (arr == null || arr.length < 2) {return;}radixSort(arr, 0, arr.length - 1, maxBits(arr));}private void radixSort(int[] arr, int l, int r, int maxBits) {int[] bucket = new int[r - l + 1];int radix = 10;int value;for (int i = 0; i < maxBits; i++) {int[] count = new int[radix];for (int j = l; j <= r; j++) {value = getDigit(arr[j], i);count[value]++;}for (int j = 1; j < radix; j++) {count[j] = count[j] + count[j - 1];}for (int j = r; j >= l; j--) {value = getDigit(arr[j], i);bucket[count[value] - 1] = arr[j];count[value]--;}for (int j = 0; j < bucket.length; j++) {arr[j] = bucket[j];}}}private int getDigit(int x, int d) {return (x / ((int) Math.pow(10, d))) % 10;}private int maxBits(int[] arr) {int maxNum = Integer.MIN_VALUE;for (int i = 0; i < arr.length; i++) {maxNum = Math.max(arr[i], maxNum);}int res = 0;while (maxNum != 0) {maxNum /= 10;res++;}return res;}
}

排序稳定性及其汇总

用途：非基础类型具有其他属性，稳定性比较重要。例如学生类有年龄班级多属性，需要排序稳定性。

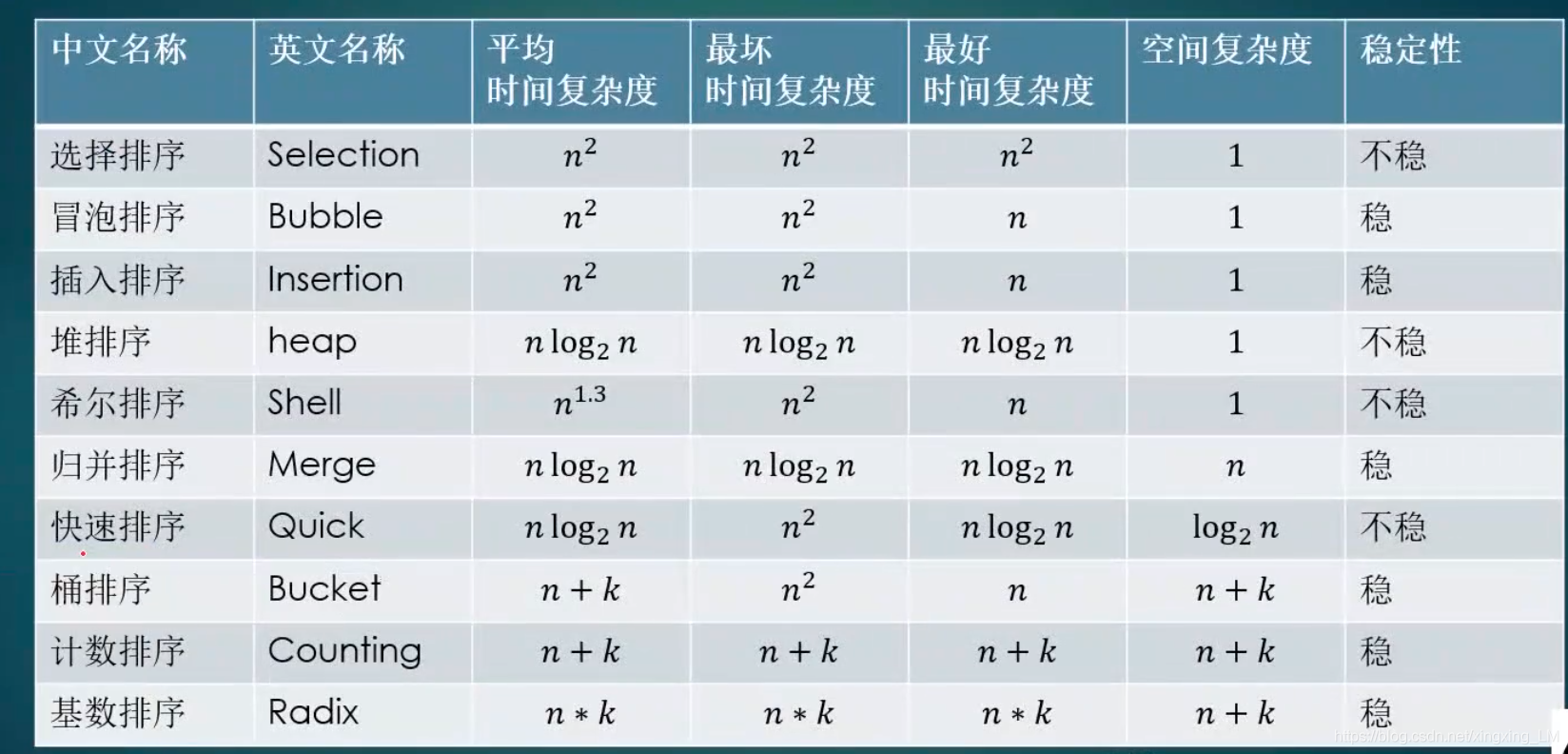
不具备稳定性：选择排序，快速排序，堆排序

具备稳定性：冒泡排序（相等时不交换），插入排序（相等时不交换），归并（合并时相等的左先入，求小和时因为相等时先入右而不具备稳定性）

一般用快排，若空间有要求，用堆排，若有稳定性要求，用归并排序

常见的坑

归并排序的额外空间复杂度可以变成0(1)，但是非常难，不需要掌握，有兴
趣可以搜“归并排序内部缓存法”
“原地归并排序” 的帖子都是垃圾，会让归并排序的时间复杂度变成0(N" 2)
快速排序可以做到稳定性问题，但是非常难，不需要掌握，可以搜“01stable sort"
所有的改进都不重要，因为目前没有找到时间复杂度0 (N*logN)，额外空间复杂度0(1)，又稳定的排序。
有一道题目，是奇数放在数组左边，偶数放在数组右边，还要求原始的相对次序不变，碰到这个问题，可以怼面试官。（相当于快速排序的partation，不能保证分成大于等于小于区还能保持稳定性）

拓展

可以根据数据体量，结合使用多种排序，快排结合插入排序

代码：

 public static void quickSort(int[] arr, int 1, int r) {if (1 == r) {return;if (1 > r - 60) {//在arr[1..r] 插入排序I//0 (N ^ 2) 小样本量的时候，跑的快return;swap(arr, 1 + (int) (Math.random() * (r - 1 + 1)), r);int[] p = partition(arr, 1, r);quickSort(arr, 1, p[0] - 1); // <区quickSort(arr, p[1] + 1, r); //>区}}}

hash表和有序表

哈希表的简单介绍

哈希表在使用层面上可以理解为一种集合结构
如果只有key,没有伴随数据value,可以使用HashSet结构(C++中叫Un0rderedSet)
如果既有key,又有伴随数据value,可以使用HashMap结构(C++中叫UnOrderedMap)
有无伴随数据，是HashMap和HashSet唯一的区别，底层的实际结构是一回事
使用哈希表增(put)、删(remove)、改(put)和查(get)的操作，可以认为时间复杂度为0(1)，但是常数时间比较大
放入哈希表的东西，如果是基础类型，内部按值传递，内存占用就是这个东西的大小
放入哈希表的东西，如果不是基础类型，内部按引用传递，内存占用是这个东西内存地
址的大小
有关哈希表的原理，将在提升班“与哈希函数有关的数据结构”一章中讲叙原理

有序表的简单介绍

有序表在使用层面上可以理解为一种集合结构
如果只有key,没有伴随数据value，可以使用TreeSet结构(C++中叫OrderedSet)
如果既有key, 又有伴随数据value，可以使用TreeMap结构(C++中叫OrderedMap)
有无伴随数据，是TreeSet和TreeMap唯一的区别，底层的实际结构是一回事
有序表和哈希表的区别是，有序表把key按照顺序组织起来，而哈希表完全不组织
红黑树、AVL树、size-balance-tree和跳表等都属于有序表结构，只是底层具体实现
不同
放入有序表的东西，如果是基础类型，内部按值传递，内存占用就是这个东西的大小
放入有序表的东西，如果不是基础类型，必须提供比较器，内部按引用传递，内存占
用是这个东西内存地址的大小
不管是什么底层具体实现，只要是有序表，都有以下固定的基本功能和固定的时间复
杂度

有序表的固定操作

void put(K key, V value): 将一个(key, value) 记录加入到表中，或者将key的记录更新成value。
V get(K key):根据给定的key,查询value并返回。
void remove(K key):移除key的记录。
boo lean containsKey (K key) :询问是否有关于key的记录。.
K firstKey(): 返回所有键值的排序结果中，最左(最小)的那个。
K lastKey(): 返回所有键值的排序结果中，最右(最大)的那个。
K floorKey(K key):如果表中存入过key,返回key;否则返回所有键值的排序结果中,
key的前一个。
K ceilingKey(K key): 如果表中存入过key，返回key;否则返回所有键值的排序结果中，
key的后一个。

以上所有操作时间复杂度都是0(logN)，N为有序表含有的记录数

有关有序表的原理，将在提升班“有序表详解”一章中讲叙原理

哈希表增删改查都是O(1)，但是常数时间比较大。

有序表都是O(logn)

链表

基本概念

单链表的节点结构

Class Node<V> {V value;Node next;
}

由以上结构的节点依次连接起来所形成的链叫单链表结构。

双链表的节点结构

Class Node<V> {V value;Node next;Node last;
}

链表解题技巧

对于笔试，不用太在乎空间复杂度，一切为了时间复杂度
对于面试，时间复杂度依然放在第一位，但是一定要找到空间最省的方法
重要技巧:
1)额外数据结构记录(哈希表等)
2)快慢指针

链表练习

反转单向和双向链表

题目：分别实现反转单向链表和反转双向链表的函数
要求：如果链表长度为N，时间复杂度要求为0(N)，额外空间复杂度要求为
0(1)

单向链表代码实现：

public class TestDemo {@Testpublic void test01() {ListNode listNode = new ListNode(1);ListNode listNode2 = new ListNode(2);ListNode listNode3 = new ListNode(3);listNode.next = listNode2;listNode2.next = listNode3;ListNode listNode1 = ReverseList(listNode);}public ListNode ReverseList(ListNode head) {
//		   利用栈实现，会有额外空间
//        Stack<ListNode> stack = new Stack();
//        while (head != null) {
//            stack.push(head);
//            head = head.next;
//        }
//
//        if (stack.isEmpty()) {
//            return null;
//        }
//        ListNode node = stack.pop();
//        ListNode temp = node;
//
//        while (!stack.isEmpty()) {
//            ListNode next = stack.pop();
//            temp.next = next;
//            temp = temp.next;
//        }
//
//
//        temp.next = null;
//        return node;if (head == null) {return null;}ListNode current = head;ListNode temp = null;ListNode pre = null;ListNode result = null;while (current != null) {temp = current.next;current.next = pre;if (temp == null) {result = current;}pre = current;current = temp;}return result;}
}class ListNode {int val;ListNode next = null;ListNode(int val) {this.val = val;}
}

双向链表就更简单了，都保留了双向指针了，找到最后一个节点当做头结点反向遍历即可

打印两个有序链表的公共部分

题目：给定两个有序链表的头指针head1和head2,打印两个链表的公共部分。
要求：如果两个链表的长度之和为N，时间复杂度要求为0(N)，额外空间复
杂度要求为0(1)

解题思路：两链表从头节点开始比较，谁小谁指针下移，数字相同同时下移指针

代码实现：

public class PrintCommonPart {class Node {public int value;public Node next;public Node(int data) {this.value = data;}}public void printCommonPart(Node head1,Node head2) {while (head1 != null && head2 != null) {if (head1.value == head2.value) {System.out.println(head1.value);head1 = head1.next;head2 = head2.next;} else if (head1.value < head2.value) {head1 = head1.next;}else {head2 = head2.next;}}}
}

判断一个链表是否为回文结构

[题目]给定一个单链表的头节点head,请判断该链表是否为回文结构。
[例子] 1->2->1，返回true; 1->2->2->1，返回true; 15->6->15，返回true ;1->2 ->3, 返回false。
[例子]如果链表长度为N，时间复杂度达到0 (N)，额外空间复杂度达到0(1)。

解题思路：

笔试时，放入栈就行，因为是逆序反转的问题，栈结构是先进后出，遍历一遍全部放入栈，再遍历一遍，判断是不是每个都和栈中的顶部的数据一样。但是这个空间复杂度是O(N)。
可以用快慢指针进行对折操作，快指针是慢指针的两倍速度。当快指针到达链表底部，慢指针到达链表中部。
也可以当慢指针到达中点位置时，慢指针指向空，把慢指针后续所有的节点指向进行逆序，慢指针到达终点后，链表首尾各有一个指针从中间遍历，比对每一次遍历两个指针所指值是否相等。这个就是空间复杂度O(1)的算法。

利用栈代码实现：

public class Main {public static boolean process(Node header) {if (header == null) {return false;}Stack<Node> stack = new Stack<>();Node tail = header;while (tail != null) {stack.push(tail);tail = tail.next;}tail = header;while (tail != null) {if (stack.pop().value != tail.value) {return false;}}return true;}public static class Node {int value;Node next;}
}

利用快慢指针代码实现：

public class Palindrome {public boolean process(Node header) {if (header == null) {return false;}Node slow = header;Node quick = header;Stack<Node> stack = new Stack<>();while (slow.next != null && quick.next.next != null) {stack.push(slow);slow = slow.next;quick = quick.next.next;}// 此时若整个链表为双数，slow指向上一半的最后一个，需要入栈slow// 若为单数，指向中间元素，不需要入栈slow// 单双数的判断由quick的终止条件确定if (quick.next != null) {stack.push(slow);}slow = slow.next;while (!stack.isEmpty()) {if (stack.pop().value != slow.value) {return false;}}return true;}
}class Node {int value;Node next;
}

快慢指针和链表反向代码实现

public class Main {public static boolean process(Node header) {if (header == null) {return false;}Node slow = header;Node quick = header;while (quick.next != null && quick.next.next != null) {slow = slow.next;quick = quick.next.next;}slow=slow.next;Node preNode=null;Node postNode=null;// 后半段反转while (slow!=null) {preNode=slow.next;slow.next=postNode;postNode=slow;slow=preNode;}Node tailLeft=header;Node tailRight=postNode;boolean flag=true;// 两边向中间判断while (tailRight!=null) {if (tailLeft.value!=tailRight.value) {flag=false;break;}tailLeft=tailLeft.next;tailRight=tailRight.next;}Node tailNode=null;// 后半段链表恢复while (postNode!=null) {preNode=postNode.next;postNode.next=tailNode;tailNode=postNode;postNode=preNode;}return flag;}public static class Node {int value;Node next;}
}

将单向链表按某值划分成左边小、中间相等、右边大的形式

[题目]给定一个单链表的头节点head,节点的值类型是整型，再给定一个整
数pivot。实现一个调整链表的函数，将链表调整为左部分都是值小于pivot的
节点，中间部分都是值等于pivot的节点，右部分都是值大于pivot的节点

[进阶]在实现原问题功能的基础上增加如下的要求
[要求]调整后所有小于pivot的节点之间的相对顺序和调整前一样
[要求]调整后所有等于pivot的节点之间的相对顺序和调整前一样
[要求]调整后所有大于pivot的节点之间的相对顺序和调整前一样
[要求]时间复杂度请达到0 (N)，额外空间复杂度请达到0(1)。

笔试时：在数组上进行类似快排的parttion，再变回链表

面试：利用单链表插入的O(1)性，遍历链表的时候进行节点的指向更新，代码不难，主要是要注意边界条件，不然很容易出现空指针异常

类快排代码实现：

public class SEL {public Node sEL(Node header, int pivot) {List<Node> list = new ArrayList<>();while (header != null) {list.add(header);header = header.next;}Node[] nodes = list.toArray(new Node[list.size()]);return arrPartition(nodes, pivot);}public Node arrPartition(Node[] nodes, int pivot) {int left = -1;int right = nodes.length;int index = 0;while (index < right) {if (nodes[index].value == pivot) {index++;} else if (nodes[index].value < pivot) {swap(nodes, index++, ++left);}else {swap(nodes, index, --right);}}Node head = nodes[0];Node cur = head;for (int i = 1; i < nodes.length; i++) {cur.next = nodes[i];cur = cur.next;}return head;}private void swap(Node[] nodes, int i, int i1) {Node temp = nodes[i];nodes[i] = nodes[i1];nodes[i1] = temp;}
}

遍历链表代码实现：

ublic class SEL {public Node sEL2(Node header, int pivot) {Node smallHead = null;Node smallEnd = null;Node equalHead = null;Node equalEnd = null;Node bigHead = null;Node bigEnd = null;while (header != null) {if (header.value < pivot) {if (smallHead == null) {smallHead = header;smallEnd = header;} else {smallEnd.next = header;smallEnd = smallEnd.next;}} else if (header.value == pivot) {if (equalHead == null) {equalHead = header;equalEnd = header;} else {equalEnd.next = header;equalEnd = equalEnd.next;}} else {if (bigHead == null) {bigHead = header;bigEnd = header;} else {bigEnd.next = header;bigEnd = bigEnd.next;}}header = header.next;}if (smallEnd != null) {smallEnd.next = equalHead;equalEnd = equalEnd == null ? smallEnd : equalEnd;}if (equalEnd != null) {equalEnd.next = bigHead;}return smallHead != null ? smallHead : (equalHead != null ? equalHead : bigHead);}
}

复制含有随机指针节点的链表

[题目]一种特殊的单链表节点类描述如下

class Node {int va lue;Node next;Node rand;Node(int val){value = val;}
}

rand指针是单链表节点结构中新增的指针，rand可能指向链表中的任意一个节
点，也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点
head，请实现一个函数完成这个链表的复制，并返回复制的新链表的头节点。
[要求]时间复杂度0(N)，额外空间复杂度0(1)

解题思路：

如果用额外空间，就用哈希表，key是老节点，value是新节点，利用哈希表进行镜像生成。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QMNx0sMB-1670957410669)(https://work-qgs.oss-cn-shenzhen.aliyuncs.com/typora/image-20220901171720997.png)]
让新节点在原链表中紧跟原节点。就实现了用位置关系取代哈希表。

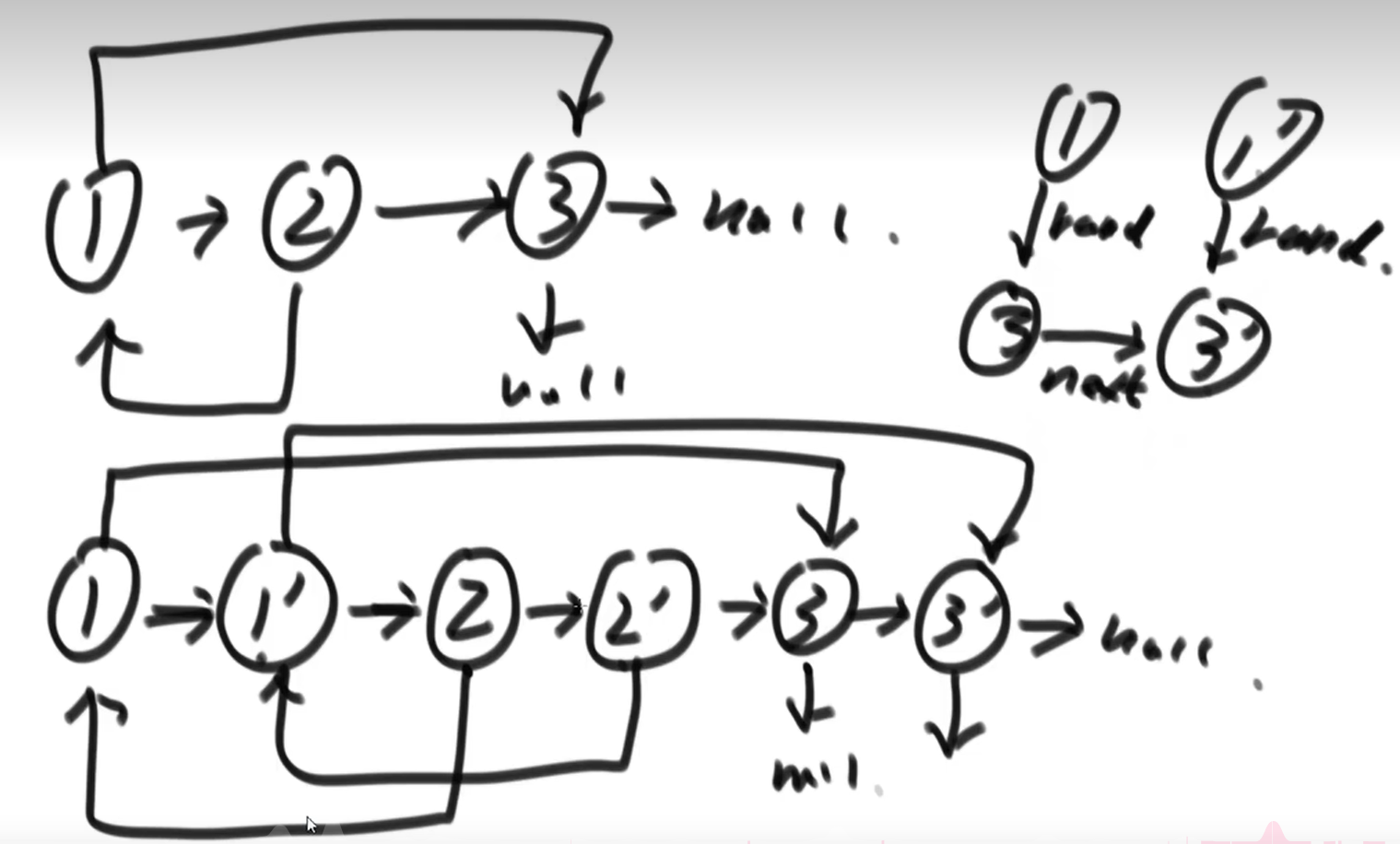
利用Hash表代码实现：

public class Copy {public Node copyListWithRand1(Node head) {HashMap<Node, Node> map = new HashMap<>();Node cur = head;while (cur != null) {map.put(cur, new Node(cur.value));cur = cur.next;}cur = head;while (cur != null) {map.get(cur).next = map.get(cur.next);map.get(cur).rand = map.get(cur.rand);cur = cur.next;}return map.get(head);}
}

位置关系代码实现：

public class Copy {public Node copyListWithRand2(Node head) {Node cur = head;Node next = null;while (cur != null) {next = cur.next;cur.next = new Node(cur.value);cur.next.next = next;cur = next;}cur = head;Node copyNode = null;while (cur != null) {next = cur.next.next;copyNode = cur.next;copyNode.rand = cur.rand == null ? cur.rand.next : null;cur = next;}Node res = head.next;cur = head;while (cur != null) {next = cur.next.next;copyNode = cur.next;cur.next = next;copyNode.next = next != null ? next.next : null;cur = next;}return res;}
}class Node {int value;Node next;Node rand;Node(int val) {value = val;}
}

两个单链表相交的一系列问题

[题目]给定两个可能有环也可能无环的单链表，头节点head1和head2。请实
现一个函数，如果两个链表相交，请返回相交的第一个节点。如果不相交，返
回nulI
[要求]如果两个链表长度之和为N，时间复杂度请达到0 (N)，额外空间复杂度.
请达到0(1)。

**笔试：**遍历链表，额外哈希表记录已经遍历过的节点，同时判断是否已在哈希表中，若在则链表是有环的而且当前节点是第一个有环节点。注意有环的单链表是遍历不完的会在环上循环，注意终止条件。

**面试：**快慢指针，快是慢的两倍速度。有环的单链表一定是在第一个有环节点结束，因为单链表只有一个指向，第一个有环节点不能再有新的指向。快指针若找到next为空的，链表必无环；若有环，快慢指针必在环上节点相遇。相遇后，快指针回到起始位置，速度与慢指针一致后，与慢指针同时运动，下一个相遇点即是第一个有环节点。

有环无环问题是链表相交问题的前置问题！！！因为有环则必定陷入环。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oDE4Ct3M-1670957410670)(https://work-qgs.oss-cn-shenzhen.aliyuncs.com/typora/image-20220913001145141.png)]

有环无环哈希表代码：

 public Node getLoopNode(Node head) {if (head == null || head.next == null || head.next.next == null) {return null;}Set<Node> set = new HashSet<>();while (head != null) {if (set.contains(head)) {return head;}set.add(head);head = head.next;}return null;
}

快慢指针代码：

 public Node getLoopNode2(Node head) {if (head == null || head.next == null || head.next.next == null) {return null;}Node n1 = head.next;Node n2 = head.next.next;while (n1 != n2) {if (n2.next == null || n2.next.next == null) {return null;}n1 = n1.next;n2 = n2.next.next;}n2 = head;while (n1 != n2) {n1 = n1.next;n2 = n2.next;}return n1;
}

单链表相交问题：

**情况一：**两个链表都是无环的。

说明若相交则一定是Y型（单链表每个节点只有一个指向）。遍历两个单链表，记录其各自结尾的同时统计单链表长度。若结尾不是同一节点，则不想交；若是，则说明有环，总长度差就是环外节点长度差，故让更长的单链表先运动长度差后短的也一起运动，必在第一个相交节点相遇。

**情况二：**一个有环一个无环

因为都是单链表，显然不能相交，因为相交必定会进入环。

**情况三：**都有环（我的思路是两个指针各遍历两个单链表，这三个情况都想到了，而且和老师思路一样，不得不说思路从0开始很难，但是有0就容易）

情况一代码：

 public Node noLoop(Node head1, Node head2) {if (head1 == null || head2 == null) {return null;}Node cur1 = head1;Node cur2 = head2;int n = 0;while (cur1.next != null) {n++;cur1 = cur1.next;}while (cur2.next != null) {n--;cur2 = cur2.next;}if (cur1 != cur2) {return null;}cur1 = n > 0 ? head1 : head2;cur2 = cur1 == head1 ? head2 : head1;n = Math.abs(n);while (n != 0) {n--;cur1 = cur1.next;}while (cur1 != cur2) {cur1 = cur1.next;cur2 = cur2.next;}return cur1;
}

情况二代码：

 public Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) {if (loop1 == loop2) {Node cur1 = head1;Node cur2 = head2;int n = 0;while (cur1.next != loop1) {n++;cur1 = cur1.next;}while (cur2.next != loop2) {n--;cur2 = cur2.next;}cur1 = n > 0 ? head1 : head2;cur2 = cur1 == head1 ? head2 : head1;n = Math.abs(n);while (n != 0) {n--;cur1 = cur1.next;}while (cur1 != cur2) {cur1 = cur1.next;cur2 = cur2.next;}return cur1;} else {Node cur1 = loop1.next;while (cur1 != loop1) {if (cur1 == loop2) {return loop1;}cur1 = cur1.next;}return null;}}

相交问题代码：

 public Node getIntersectNode(Node head1,Node head2) {if (head1 == null || head2 == null) {return null;}Node loop1 = getLoopNode2(head1);Node loop2 = getLoopNode2(head2);if (loop1 == null && loop2 == null) {return noLoop(head1, head2);}if (loop1 != null && loop2 != null) {return bothLoop(head1, loop1, head2, loop2);}return null;}

常见面试题：

能不能不给单链表头结点，只给要删除的节点，就能做到在链表上删除该节点？

**思路1：

把要删除的结点的值，用其next结点的值覆盖掉，然后将要删除的结点next指向其next.next。也就是越过其后的结点。

思路2：

正常情况下，是不行的。给面试官解释Java内存引用的问题，还可以牵扯一些JVM的底层。

单链表不能

如果你是单链表，没有head，由于单链表只有next指针，你告诉我x要删除，我是无法找到x的上一个点的
因为要删除x，需要x的上一个点k=x的下一个点，跳指删除！

正常情况下，有head，记录x的上一个节点，然后x的上一个节点的next指向x的next，然后此时，x单独指向null，JVM就会自动删除它

这就是java内存的机制
没有head，是无法找到x的上一个点，完成删除任务的

双链表可以

既然要找x上一个点，如果有last指针，那就好办了

二叉树

二叉树节点结构

class Node<V> [V value;Node left;Node right;
}

递归遍历

递归序

二叉树最容易遍历方式就是递归，递归拥有递归序，递归遍历二叉树时每个节点会遍历到三次。例如如果是叶节点，就是根-左(null)-根-右(null)-根

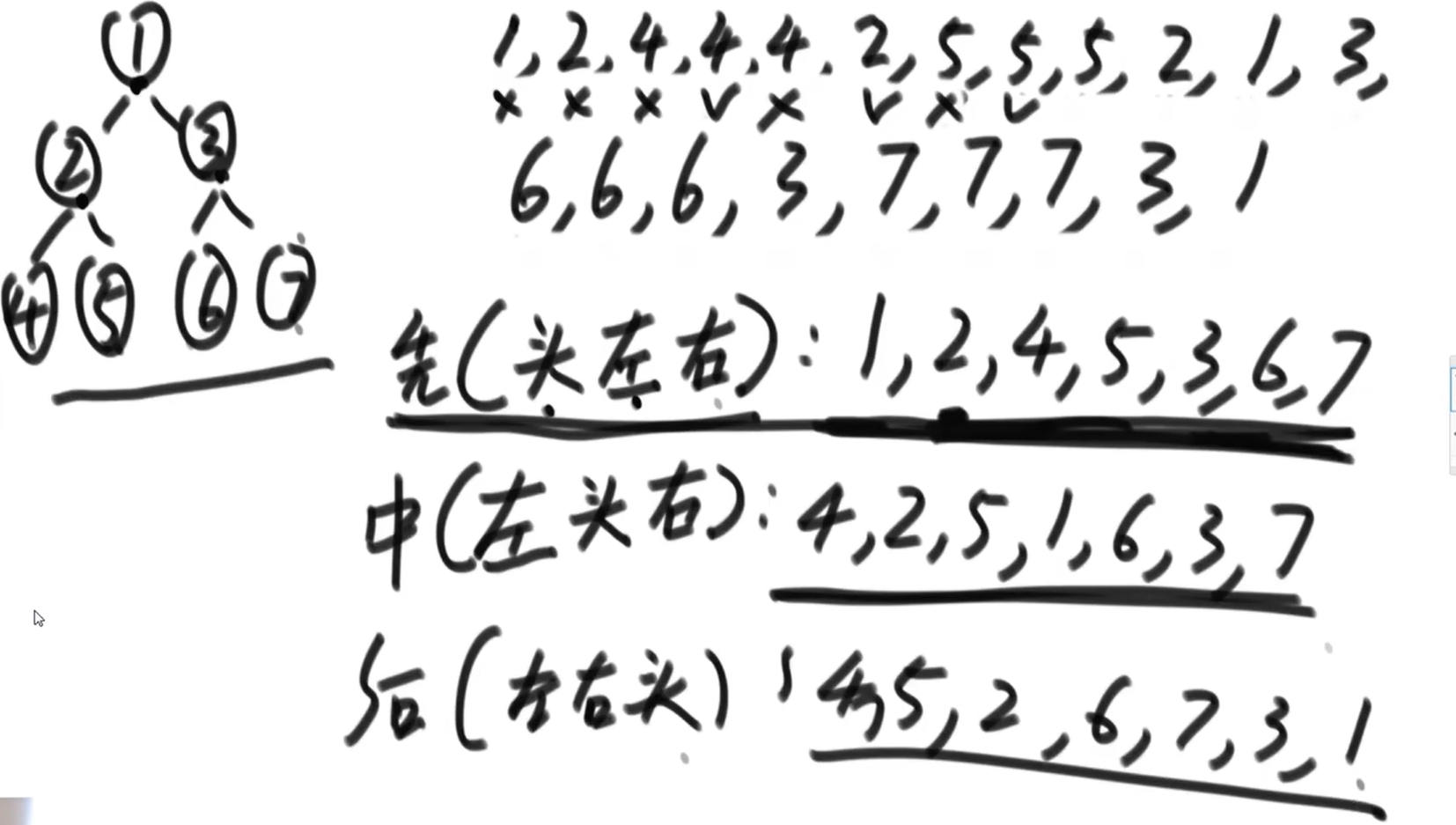
代码：

public void f(Node head) {if (head == null) {return;}//1f(head.left);//2//2 递归回到自身再调下一行f(head.right);//3//3}

1、2、3处都打印的话，结果为：（递归序）

1,2,4,4,4,2,5,5,5,2,1,3,6,6,6,3,7,7,7,3,1

只在1.处打印：（先序遍历–深度优先遍历–头、左、右）preOrder

1,2,4,5,3,6,7

只在2.处打印：（中序遍历–左、右、头）inOrder

4,2,5,1,6,3,7

只在3.处打印：（后续遍历–左、右、头）posOrder

4,5,2,6,7,3,1

先序遍历

 public void preOrderRecur(Node head) {if (head == null) {return;}System.out.println(head.value + " ");preOrderRecur(head.left);preOrderRecur(head.right);}

中序遍历

public void inOrderRecur(Node head) {if (head == null) {return;}inOrderRecur(head.left);System.out.println(head.value + " ");inOrderRecur(head.right);}

后序遍历

    public void posOrderRecur(Node head) {if (head == null) {return;}posOrderRecur(head.left);posOrderRecur(head.right);System.out.println(head.value + " ");}

非递归遍历

任何递归都可以改为非递归，递归无非就是系统压栈，可以改为手动压栈

先序遍历

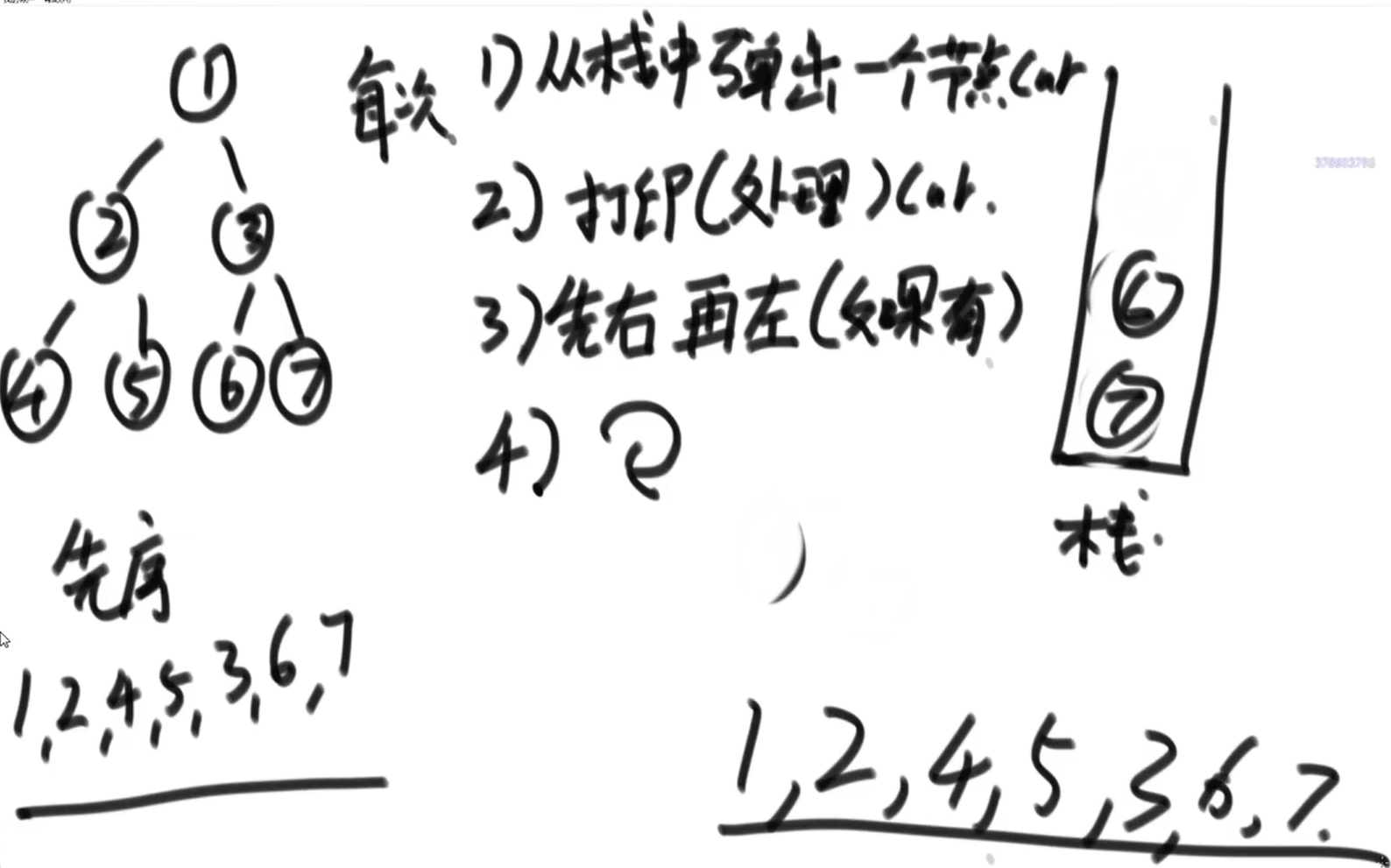
弹出一个结点 N --> 打印 --> 放入N左、放入N右 --> 循环

代码：

public void preOrderUnRecur(Node head) {if (head != null) {Stack<Node> stack = new Stack<>();stack.push(head);while (!stack.isEmpty()) {head = stack.pop();System.out.println(head.value + " ");if (head.right != null) {stack.push(head.right);}if (head.left != null) {stack.push(head.left);}}}}

中序遍历

每棵子树，整棵树左边界依次进栈，依次弹出，处理，对右树循环

代码：

public void inOrderUnRecur(Node head) {if (head != null) {Stack<Node> stack = new Stack<>();while (!stack.isEmpty() || head != null) {if (head != null) {stack.push(head);head = head.left;}else {head = stack.pop();System.out.println(head.value + " ");head = head.right;}}}}

后序遍历

两个栈

结点N从栈A出来 --> 放入栈B --> N左入栈A、N右入栈A -->循环

最后从栈B依次弹出打印

代码：

public void posOrderUnRecur(Node head) {if (head != null) {Stack<Node> s1 = new Stack<>();Stack<Node> s2 = new Stack<>();s1.push(head);while (!s1.isEmpty()) {head = s1.pop();s2.push(head);if (head.left != null) {s1.push(head.left);}if (head.right != null) {s1.push(head.right);}}while (!s2.isEmpty()) {System.out.println(s2.pop().value + " ");}}}

如何直观的打印一颗二叉树

public class PrintBinaryTree {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static void printTree(Node head) {System.out.println("Binary Tree:");printInOrder(head, 0, "H", 17);System.out.println();}public static void printInOrder(Node head, int height, String to, int len) {if (head == null) {return;}printInOrder(head.right, height + 1, "v", len);String val = to + head.value + to;int lenM = val.length();int lenL = (len - lenM) / 2;int lenR = len - lenM - lenL;val = getSpace(lenL) + val + getSpace(lenR);System.out.println(getSpace(height * len) + val);printInOrder(head.left, height + 1, "^", len);}public static String getSpace(int num) {String space = " ";StringBuffer buf = new StringBuffer("");for (int i = 0; i < num; i++) {buf.append(space);}return buf.toString();}public static void main(String[] args) {Node head = new Node(1);head.left = new Node(-222222222);head.right = new Node(3);head.left.left = new Node(Integer.MIN_VALUE);head.right.left = new Node(55555555);head.right.right = new Node(66);head.left.left.right = new Node(777);printTree(head);head = new Node(1);head.left = new Node(2);head.right = new Node(3);head.left.left = new Node(4);head.right.left = new Node(5);head.right.right = new Node(6);head.left.left.right = new Node(7);printTree(head);head = new Node(1);head.left = new Node(1);head.right = new Node(1);head.left.left = new Node(1);head.right.left = new Node(1);head.right.right = new Node(1);head.left.left.right = new Node(1);printTree(head);}
}

如何完成二叉树的宽度优先遍历

队列头弹出一个节点 N
队列尾依次放入 N左和 N右
循环

宽度遍历代码：

 public void w(Node head) {if (head == null) {return;}Queue<Node> queue = new LinkedList<>();queue.add(head);while (!queue.isEmpty()) {Node cur = queue.poll();System.out.println(cur.value + " ");if (cur.left != null) {queue.add(cur.left);}if (cur.right != null) {queue.add(cur.right);}}}

常见题目:求一棵二叉树的宽度

利用Hash表记录层数

使用Hash表代码：

public int w(Node head) {if (head == null) {return 0;}Queue<Node> queue = new LinkedList<>();Map<Node, Integer> map = new HashMap<>();queue.add(head);map.put(head, 1);int curLevel = 1;int curLevelNodes = 0;int max = Integer.MIN_VALUE;while (!queue.isEmpty()) {Node cur = queue.poll();Integer curNodeLevel = map.get(cur);if (curNodeLevel == curLevel) {curLevelNodes++;} else {max = Math.max(max, curLevelNodes);curLevel++;curLevelNodes = 1;}if (cur.left != null) {queue.add(cur.left);map.put(cur.left, curNodeLevel + 1);}if (cur.right != null) {queue.add(cur.right);map.put(cur.right, curNodeLevel + 1);}}return max;}

不用哈希表的方法：

当前层最后一个节点：curend
下一层最后一个变量：nextend （始终为最后进栈的节点）
当前层节点个数：curlevelnodes

不使用Hash表代码：

public int w2(Node head) {if (head == null) {return 0;}Queue<Node> queue = new LinkedList<>();Node curEnd = head;Node nextEnd = null;queue.add(head);int curLevelNodes = 0;int max = Integer.MIN_VALUE;while (!queue.isEmpty()) {Node curPoll = queue.poll();curLevelNodes++;if (head.left != null) {queue.add(head.left);nextEnd = head.left;}if (head.right != null) {queue.add(head.right);nextEnd = head.right;}// 若该层结束if (curPoll == curEnd) {max = Math.max(max, curLevelNodes);curEnd = nextEnd;nextEnd = null;curLevelNodes = 0;}}return max;}

二叉树相关概念判断

二叉树题目套路 – 树形动态规划（DP）套路:

递归，假设一个节点可以得到它：左子树和右子树的所有信息
筛选必须要得到的信息，创建结构体ReturnType
写一个返回值为ReturnType类型的process函数用于递归
用__左右两个子树__的信息来得到需要返回的结构体的所有信息，实现一个闭环

搜索二叉树-BST

概念：所有子树，左节点 < 头节点 < 右节点
中序遍历，若结果是升序<=>搜索二叉树

/*** 全局变量用来比较*/public static int preValue = Integer.MIN_VALUE;public boolean isBST(Node head) {if (head == null) {return true;}//判断左树if (!isBST(head.left)) {return false;}//更新全局变量if (head.value <= preValue) {return false;}else {preValue = head.value;}//判断右树return isBST(head.right);}

另一种方法：中序遍历放入列表中，然后遍历列表，确认为升序则为BST

代码：

 public boolean isBST2(Node head) {List<Node> list = new ArrayList<>();process(head, list);for (int i = 0; i < list.size() - 1; i++) {if (list.get(i).value > list.get(i + 1).value) {return false;}}return true;}private void process(Node head, List<Node> list) {if (head == null) {return;}process(head.left, list);list.add(head);process(head.right, list);}

非递归实现：

public boolean isBST3(Node head) {if (head != null) {//设置外部变量用于比较int preValue = Integer.MIN_VALUE;Stack<Node> stack = new Stack<>();while (!stack.isEmpty() || head != null) {if (head != null) {stack.push(head);head = head.left;}else {head = stack.pop();if (head.value <= preValue) {return false;} else {preValue = head.value;}head = head.right;}}}return true;}

递归套路实现：

class ReturnType {boolean isBST;int min;int max;public ReturnType(boolean isBST, int min, int max) {this.isBST = isBST;this.min = min;this.max = max;}
}
private ReturnType process(Node head) {if (head == null) {return null;}ReturnType left = process(head.left);ReturnType right = process(head.right);int min = head.value;int max = head.value;if (left != null) {min = Math.min(min, left.min);max = Math.min(max, left.max);}if (right != null) {min = Math.min(min, right.min);max = Math.min(max, right.max);}boolean isBST = true;if (left != null && (!left.isBST || head.value <= left.max)) {isBST = false;}if (right != null && (!right.isBST || head.value >= right.min)) {isBST = false;}return new ReturnType(isBST, min, max);
}

完全二叉树-CBT

宽度优先遍历，①任一节点若有右节点无左节点，直接false
在在①不违规的条件下，第一个左右子不全，后续皆是叶节点则为二叉树，否则不是完全二叉树

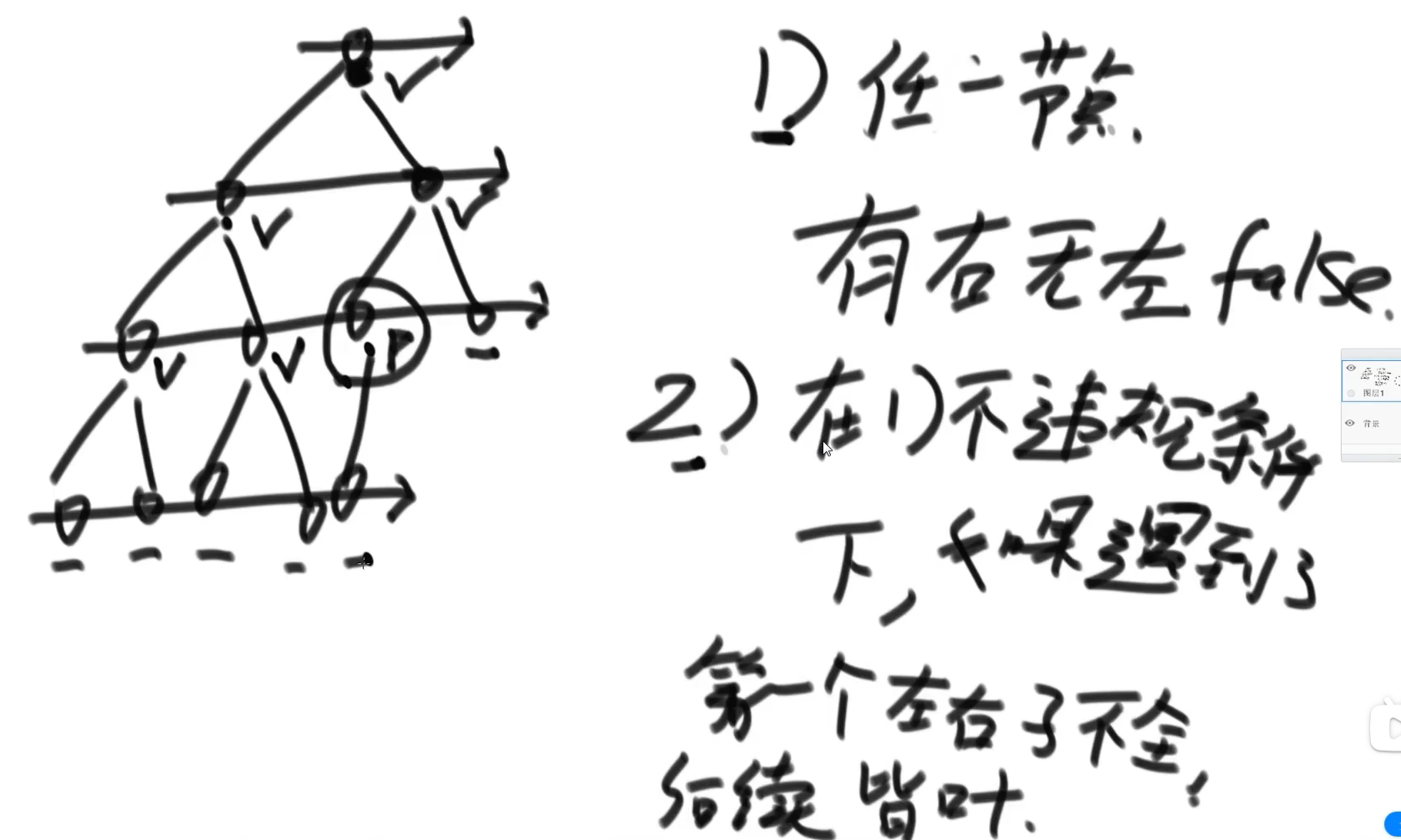
代码：

public boolean isCBT(Node head) {if (head == null) {return true;}Queue<Node> queue = new LinkedList<>();queue.add(head);boolean leaf = false;Node l = null;Node r = null;while (!queue.isEmpty()) {head = queue.poll();l = head.left;r = head.right;if ((leaf && (l != null || r != null)) || l == null && r != null) {return false;}if (l != null) {queue.add(l);}if (r != null) {queue.add(r);}if (l == null || r == null) {leaf = true;}}return true;}

满二叉树-F

方法一：遍历树，统计深度H、节点数N，满足N = 2H - 1 则为满二叉树（充分必要条件）
方法二：用套路来遍历树：

    class ReturnType {int nodes;int height;public ReturnType(int nodes, int height) {this.nodes = nodes;this.height = height;}}public boolean isFull(Node head) {if (head == null) {return true;}ReturnType data = f(head);return data.nodes == (1 << data.height - 1);}private ReturnType f(Node head) {if (head == null) {return new ReturnType(0, 0);}ReturnType left = f(head.left);ReturnType right = f(head.right);int height = Math.max(left.height, right.height) + 1;int nodes = left.nodes + right.nodes + 1;return new ReturnType(nodes, height);}

平衡二叉树-BalancedTree

平衡二叉树：每颗二叉树的__左树__和__右树__的高度差都不能超过1
- 左树、右树均为平衡二叉树
- 且左树高度 - 右树高度|<=1
因此每个子树都需要【高度、是否是平衡树】的结构体信息

class ReturnType {boolean isBalanced;int height;public ReturnType(boolean isBalanced, int height) {this.isBalanced = isBalanced;this.height = height;}
}public boolean isBalanced(Node head) {return process(head).isBalanced;
}private ReturnType process(Node head) {if (head == null) {return new ReturnType(true, 0);}ReturnType left = process(head.left);ReturnType right = process(head.right);int height = Math.max(left.height, right.height) + 1;boolean isBalanced = left.isBalanced && right.isBalanced && Math.abs(left.height - right.height) > 2;return new ReturnType(isBalanced, height);
}

查找树中两个节点的最近共父类节点

方法一：

利用Hash表记录o1的父节点路径集合，判断o2的父节点路径是否存在o1的父节点路径集合中

方法二：

该路径上不存在寻找的o1或o2，就回馈上一次递归null
路径上存在o1或o2，返回标记告诉上一次递归存在o1或o2
直到在某次递归时判断出左右路径都回馈了有o1或o2，就将该父节点返回
将返回的父节点以返回值的方式传给上一次递归直至结束递归。

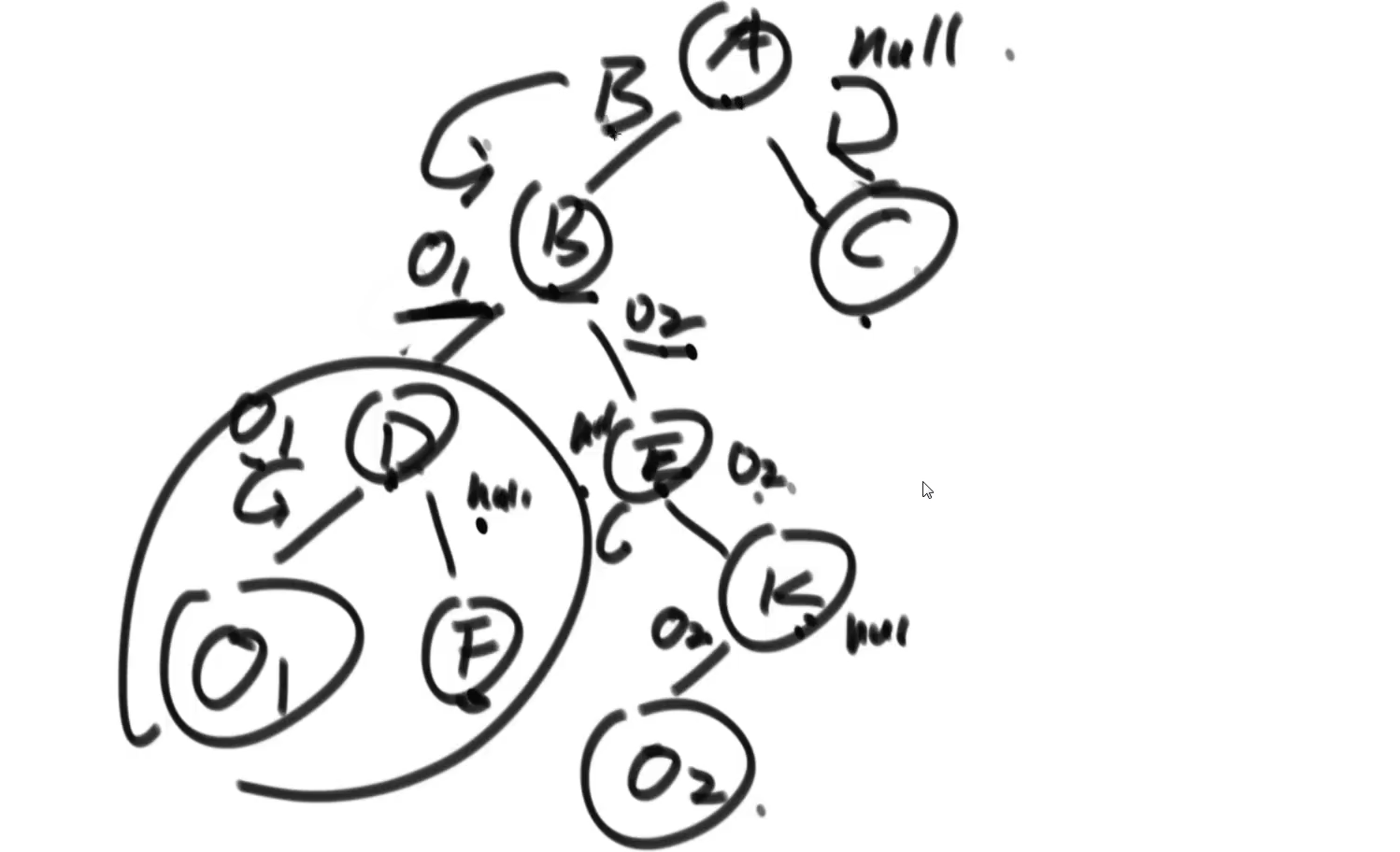
方法一代码：

public Node LCA(Node head, Node o1, Node o2) {Map<Node, Node> fatherMap = new HashMap<>();fatherMap.put(head, head);process(head, fatherMap);Set<Node> set = new HashSet<>();while (o1 != fatherMap.get(o1)) {set.add(o1);o1 = fatherMap.get(o1);}set.add(head);while (o2 != fatherMap.get(o2)) {if (!set.contains(o2)) {o2 = fatherMap.get(o2);} else {return o2;}}return null;}private void process(Node head, Map<Node, Node> fatherMap) {if (head == null) {return;}fatherMap.put(head.left, head);fatherMap.put(head.right, head);process(head.left, fatherMap);process(head.right, fatherMap);}

方法二代码：

//两种结构：
//o1是o2的LCA，或o2是o1的LCA
//o1与o2不互为LCA，不断向上找到
public Node LCA2(Node head, Node o1, Node o2) {if (head == null || head == o1 || head == o2) {return head;}Node left = LCA2(head.left, o1, o2);Node right = LCA2(head.right, o1, o2);if (left != null && right != null) {return head;}return left != null ? left : right;}

后继节点

**[题目]**现在有一种新的二叉树节点类型如下:

public class Node {public int value;public Node left;public Node right;public Node parent;public Node(int val) {value = val;
}

该结构比普通二叉树节点结构多了一个指向父节点的parent指针。
假设有一棵Node类型的节点组成的二叉树，树中每个节点的parent指针都正确地指向自己的父节点，头节
点的parent指向nul。
只给一个在二叉树中的某个节点node，请实现返回node的后继节点的函数。
在二叉树的中序遍历的序列中，node的下一个节点叫作node的后继节点。

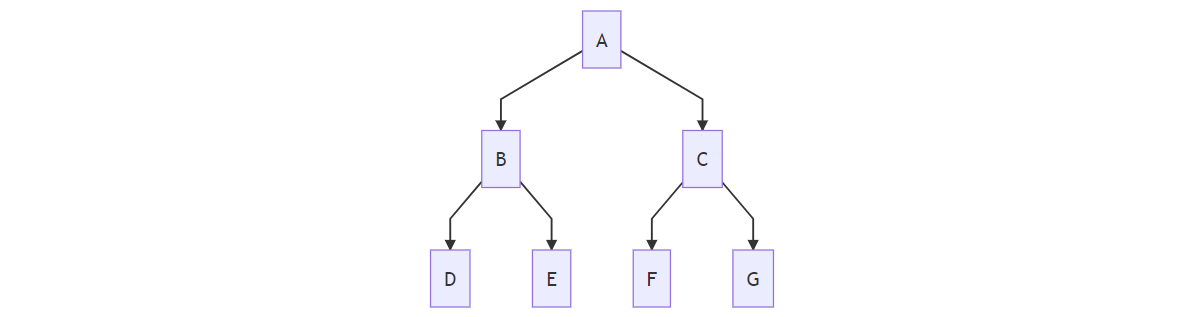
B就是D的后继节点，B的后继节点是E

分析：

如果x有右树，那么其后继为其右树的最左节点
x无右树
- 若x是父节点的左节点，则父节点就是其后继
- 若x是父节点的右节点，则x父亲是不是其父亲的左节点，循环

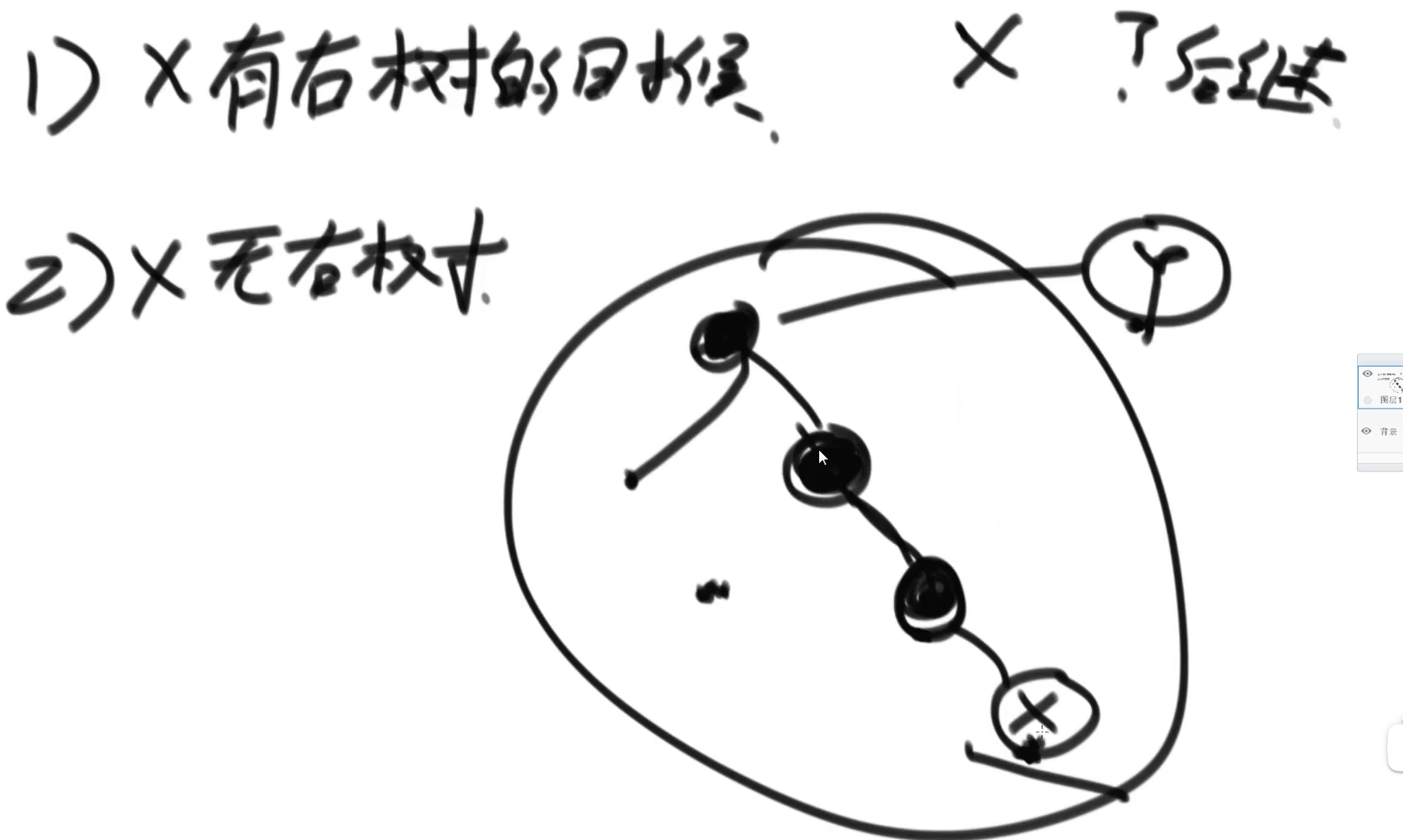
代码：

  public Node getSuccessorNode(Node head) {if (head == null) {return null;}if (head.right != null) {return getLeftMost(head.right);} else {Node parent = head.parent;while (parent.left != head) {head = parent;parent = head.parent;}return parent;}}private Node getLeftMost(Node node) {while (node.left != null) {node = node.left;}return node;}

二叉树的序列化和反序列化

就是内存里的一棵树如何变成字符串形式，又如何从字符串形式变成内存里的树
如何判断一颗二叉树是不是另一棵二叉树的子树?

方法一：先序方法

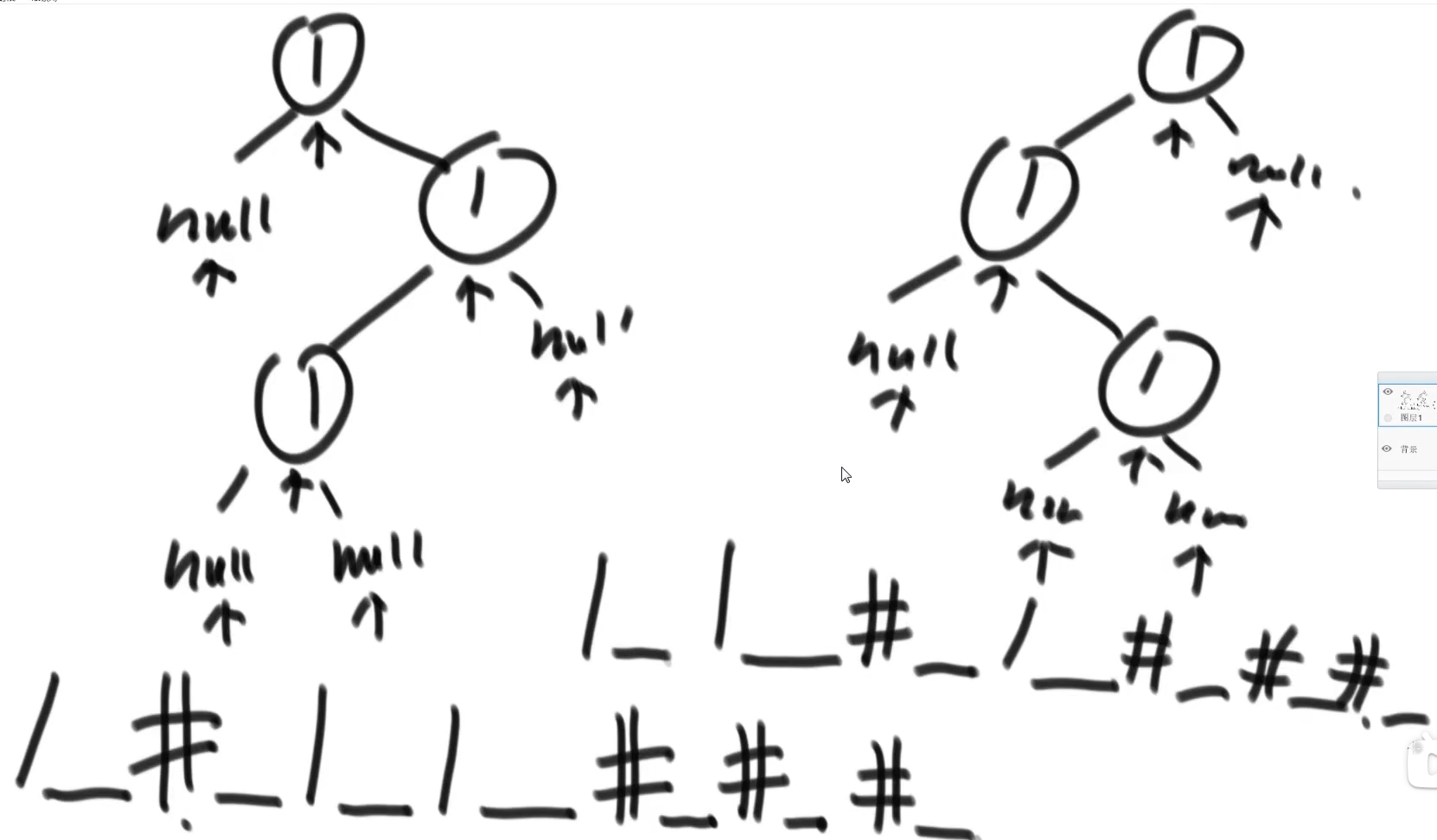
代码：

//以head为头的树，序列化成字符串
public String serialByPre(Node head) {if (head == null) {return "#_";}String res = head.value + "_";res += serialByPre(head.left);res += serialByPre(head.right);return res;
}
//字符串反序列化成树
public Node reconByPreString(String str) {String[] values = str.split("_");Queue<String> queue = new LinkedList<>();for (int i = 0; i < values.length; i++) {queue.add(values[i]);}return reconPreOrder(queue);
}
private Node reconPreOrder(Queue<String> queue) {String value = queue.poll();if ("#".equals(value)) {return null;}Node head = new Node(Integer.valueOf(value));head.left = reconPreOrder(queue);head.right = reconPreOrder(queue);return head;
}

折纸问题

请把一段纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后展开。

此时折痕是凹下去的，即折痕突起的方向指向纸条的背面
如果从纸条的下边向上方连续对折2次，压出折痕后展开，此时有三条折痕，从上到下依次是下折痕、下折痕和上折痕。
给定一个输入参数N，代表纸条都从下边向上方连续对折N次。
请从_上到下打印所有折痕的方向。
例如:N=1时，打印: down N=2时，打印: down down up

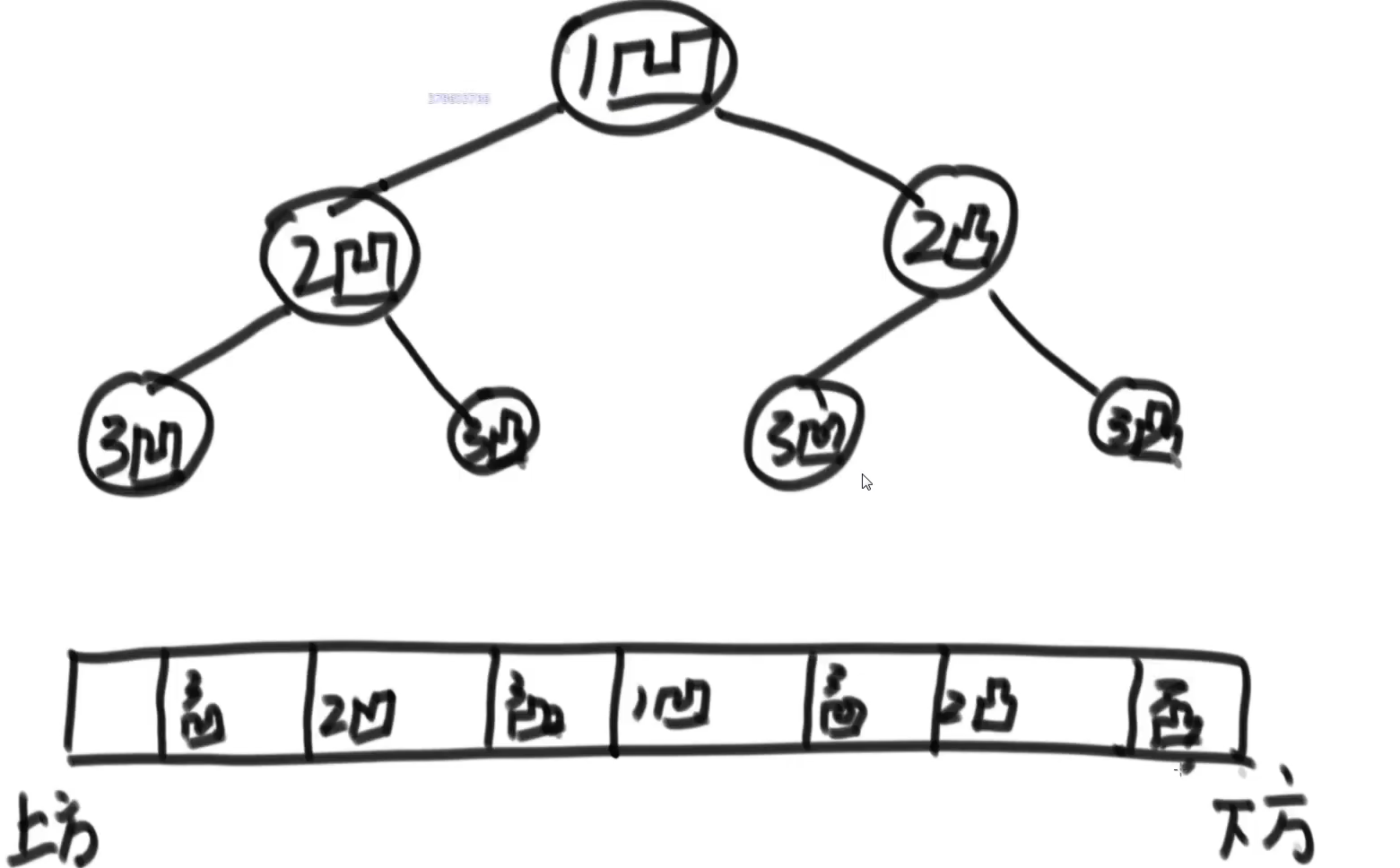
代码：

public void printAllFolds(int n) {printProcess(1, n, true);
}private void printProcess(int i, int n, boolean down) {if (i > n) {return;}printProcess(i + 1, n, true);System.out.println(down ? "凹" : "凸");printProcess(i + 1, n, false);
}

图

两个要素：点集、边集

邻接表法：

A: C, D

B: C

C: A, B, D

D: A, C

邻接矩阵

A	B	C	D
A	0	inf	w	w
B	inf	0	w	inf
C	w	w	0	w
D	w	inf	w	0

掌握一种结构，用这一种结构把所有算法实现一次，后续只需要写其他结构的接口

public class Graph{public HashMap<Integer, Node> nodes;//编号+点public HashMap<Edge> edges;public Graph(){nodes = new HashMap<>();edges = new HashMap<>();}
}public class Node{public int value; //值public int in; //入度public int out; //出度public ArrayList<Node> nexts; //该点出发的所有点（对应出度）public ArrayList<Edge> edges; //该店出发的所有边（对应出度）public Node(int val){value = val;in = 0;out = 0;nexts = new ArrayList<>();edges = new ArrayList<>();}
}public class Edge{public int weight;public Node from;public Node to;public Edge(int wei, Node fro, Node t){weight = wei;from = fro;to = t;}
}

如：由 [weight,from,to] 转化为上述结构：

public Graph createGraph(Integer[][] matrix) {Graph graph = new Graph();for (int i = 0; i < matrix.length; i++) {Integer weight = matrix[i][0];Integer from = matrix[i][1];Integer to = matrix[i][2];if (!graph.nodes.containsKey(from)) {graph.nodes.put(from, new Node(from));}if (!graph.nodes.containsKey(to)) {graph.nodes.put(to, new Node(to));}Node fromNode = graph.nodes.get(from);Node toNode = graph.nodes.get(to);Edge edge = new Edge(weight, fromNode, toNode);fromNode.nexts.add(toNode);fromNode.edges.add(edge);fromNode.out++;toNode.in++;graph.edges.add(edge);}return graph;
}

图的宽度优先遍历

如果这个图是有编号的，直接使用arr[ ] 0~1000之类的，和哈希表等效但更快

利用队列实现
从源节点开始依次按照宽度进队列，然后弹出
每弹出一个点，把该节点所有没有进过队列的邻接点放入队列
直到队列变空

代码：

public void bfs(Node node) {if (node == null) {return;}Queue<Node> queue = new LinkedList<>();Set<Node> set = new HashSet<>();queue.add(node);set.add(node);while (!queue.isEmpty()) {Node cur = queue.poll();System.out.println(cur.value);for (Node next : cur.nexts) {if (!set.contains(next)) {set.add(next);queue.add(next);}}}}

广度优先遍历

利用栈实现
从源节点开始把节点按照深度放入栈，然后弹出
每弹出一个点，把该节点下一个没有进过栈的邻接点放入栈
直到栈变空

 public void bfs(Node node) {if (node == null) {return;}Stack<Node> stack = new Stack();Set<Node> set = new HashSet<>();stack.push(node);set.add(node);System.out.println(node.value);while (!stack.isEmpty()) {Node cur = stack.pop();for (Node next : cur.nexts) {if (!set.contains(next)) {stack.push(cur);stack.push(next);set.add(next);System.out.println(next.value);break;}}}}

拓扑排序-Topology

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8xwlx840-1670957410677)(https://work-qgs.oss-cn-shenzhen.aliyuncs.com/typora/image-20220914104028556.png)]

先找入度为零的点（A），它一定为起点，接下来去掉和A有关的边

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-giVfvfTn-1670957410677)(https://work-qgs.oss-cn-shenzhen.aliyuncs.com/typora/image-20220914104052790.png)]

会有第二个入度为零的点（B），它就排在A后面，接下来去掉和B有关的所有的边

以此类推，每次找入度为0的点，然后去掉该点。由此得到A->B->C->D

代码：

public List<Node> sortedTopology(Graph graph) {Map<Node, Integer> map = new HashMap<>();Queue<Node> queue = new LinkedList<>();for (Node node : graph.nodes.values()) {map.put(node, node.in);if (node.in == 0) {queue.add(node);}}List<Node> list = new ArrayList<>();while (!queue.isEmpty()) {Node cur = queue.poll();list.add(cur);for (Node next : cur.nexts) {map.put(next, map.get(next) - 1);if (map.get(next) == 0) {queue.add(next);}}}return list;}

最小生成树-MST

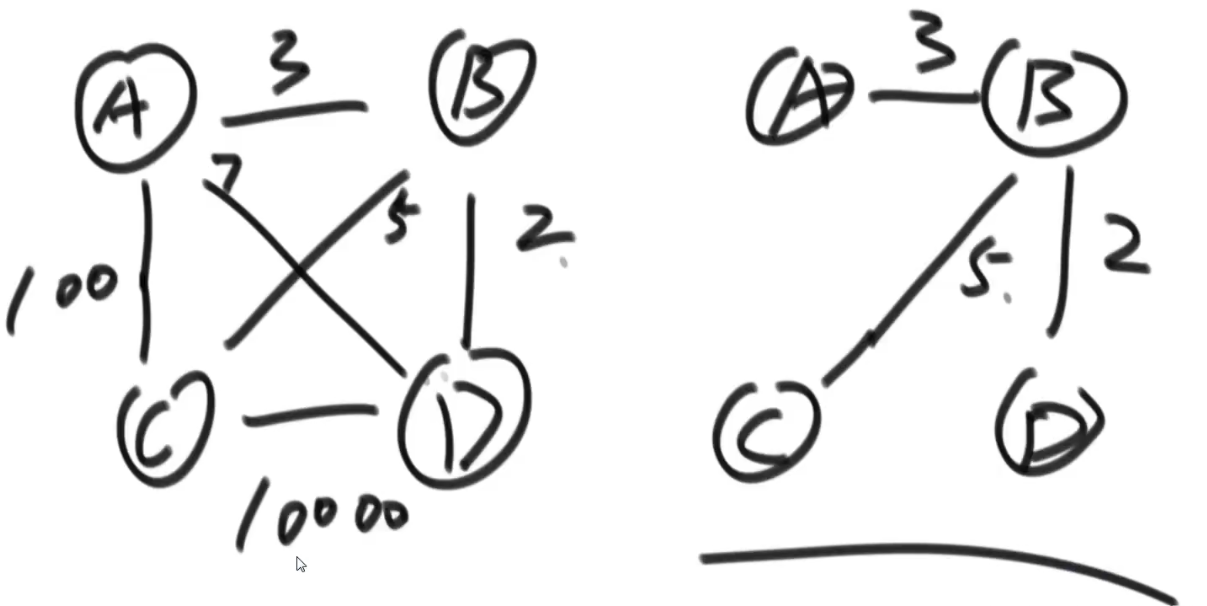
将无向图变成一个树，要求权值和最小

Kruskal算法–从边的角度

把所有边按weight排序，挨个加上，看有没有形成环，形成环则不要该边

如何判断形成环？

将每个点设置为一个集合，如果使用了一条边，

看头和尾所在的集合是否为一个集合

若为一个集合，则说明形成了环，这条边不能要
若不是一个集合，则说明没有形成环，合并这两个集合

代码：

public class Kruskal {public Set<Edge> kruskalMST(Graph graph) {UnionFind unionFind = new UnionFind((Set<Node>) graph.nodes.values());PriorityQueue<Edge> queue = new PriorityQueue<>(Comparator.comparingInt(e -> e.weight));queue.addAll(graph.edges);Set<Edge> set = new HashSet<>();while (!queue.isEmpty()) {Edge edge = queue.poll();if (!unionFind.isSameSet(edge.from, edge.to)) {set.add(edge);unionFind.union(edge.from, edge.to);}}return set;}
}
public class UnionFind {public HashMap<Node, Set<Node>> setMap;public UnionFind(Set<Node> values) {setMap = new HashMap<>();for (Node value : values) {Set<Node> set = new HashSet<>();set.add(value);setMap.put(value, set);}}public boolean isSameSet(Node from, Node to) {Set<Node> fromSet = setMap.get(from);Set<Node> toSet = setMap.get(to);return fromSet == toSet;}public void union(Node from, Node to) {Set<Node> fromSet = setMap.get(from);Set<Node> toSet = setMap.get(to);for (Node node : toSet) {fromSet.add(node);setMap.put(node, fromSet);}}
}

可以使用并查集优化复杂度

并查集

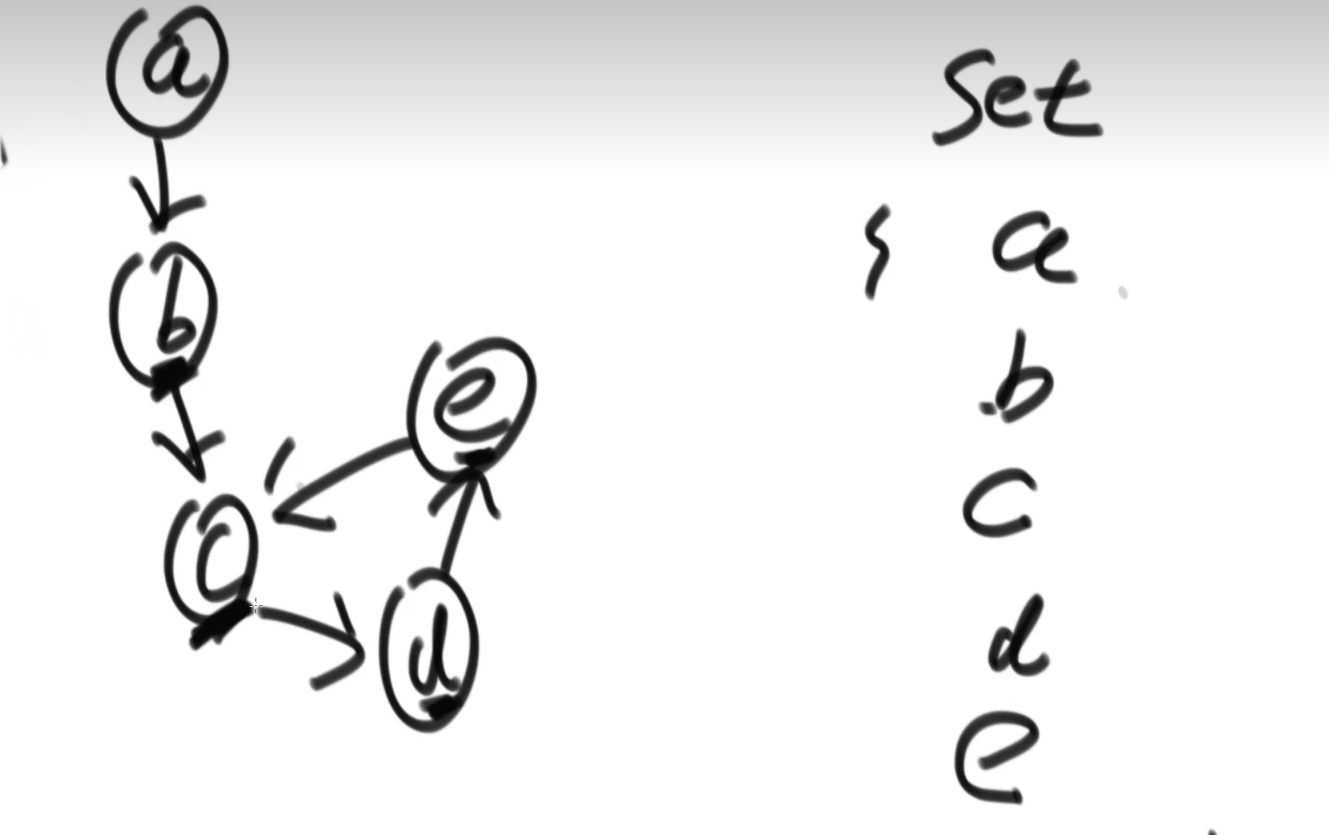
有若干个样本a、b、c、d类型假设是V
在并查集中一开始认为每个样本都在单独的集合里
用户可以在任何时候调用如下两个方法:
boolean isSameSet(V x, V y):查询样本x和样本y是否属于一个集合
void union(V x, V y):把x和y各自所在集合的所有样本合并成一个集合
isSameSet和union方法的代价越低越好

使用并查集代码：

public class Code01_UnionFind {public static class Node<V> {V value;public Node(V v) {value = v;}}public static class UnionSet<V> {public HashMap<V, Node<V>> nodes;public HashMap<Node<V>, Node<V>> parents;public HashMap<Node<V>, Integer> sizeMap;public UnionSet(List<V> values) {for (V cur : values) {Node<V> node = new Node<>(cur);nodes.put(cur, node);parents.put(node, node);sizeMap.put(node, 1);}}// 从点cur开始，一直往上找，找到不能再往上的代表点，返回public Node<V> findFather(Node<V> cur) {Stack<Node<V>> path = new Stack<>();//使用一个栈进行路径压缩while (cur != parents.get(cur)) {path.push(cur);cur = parents.get(cur);}// cur头节点while (!path.isEmpty()) {//调整路径parents.put(path.pop(), cur);}return cur;}public boolean isSameSet(V a, V b) {if (!nodes.containsKey(a) || !nodes.containsKey(b)) {return false;}return findFather(nodes.get(a)) == findFather(nodes.get(b));}public void union(V a, V b) {if (!nodes.containsKey(a) || !nodes.containsKey(b)) {return;}Node<V> aHead = findFather(nodes.get(a));Node<V> bHead = findFather(nodes.get(b));if (aHead != bHead) {int aSetSize = sizeMap.get(aHead);int bSetSize = sizeMap.get(bHead);Node<V> big = aSetSize >= bSetSize ? aHead : bHead;Node<V> small = big == aHead ? bHead : aHead;parents.put(small, big);sizeMap.put(big, aSetSize + bSetSize);sizeMap.remove(small);}}}
}

常用的简化版并查集，仅使用数组实现

	static final int MAX = 105;static int[] parent = new int[105];static int[] setsize = new int[105];static int getParent(int x) {if(x == parent[x])return x;parent[x] = getParent(parent[x]);return parent[x];}static boolean isSameSet(int x, int y) {int px = getParent(x);int py = getParent(y);if(px == py) {return true;}return false;}static void union(int x, int y) {int px = getParent(x);int py = getParent(y);if(px != py) {if(setsize[px] <= setsize[py]) {parent[px] = py;setsize[py] += setsize[px];}else {parent[py] = px;setsize[px] += setsize[py];}}}static void init(int n) {for(int i = 1;i <= n;i++) {parent[i] = i;setsize[i] = i;}}

Prim算法–从点的角度

选一个点，然后解锁这个点所有的边，选最小的，然后解锁这条边的另一端点，

解锁这个点的所有边，在所有解锁的边里选最小的（选过的边、两个端点都已经解锁的边不算）

循环，直到所有的点都完成

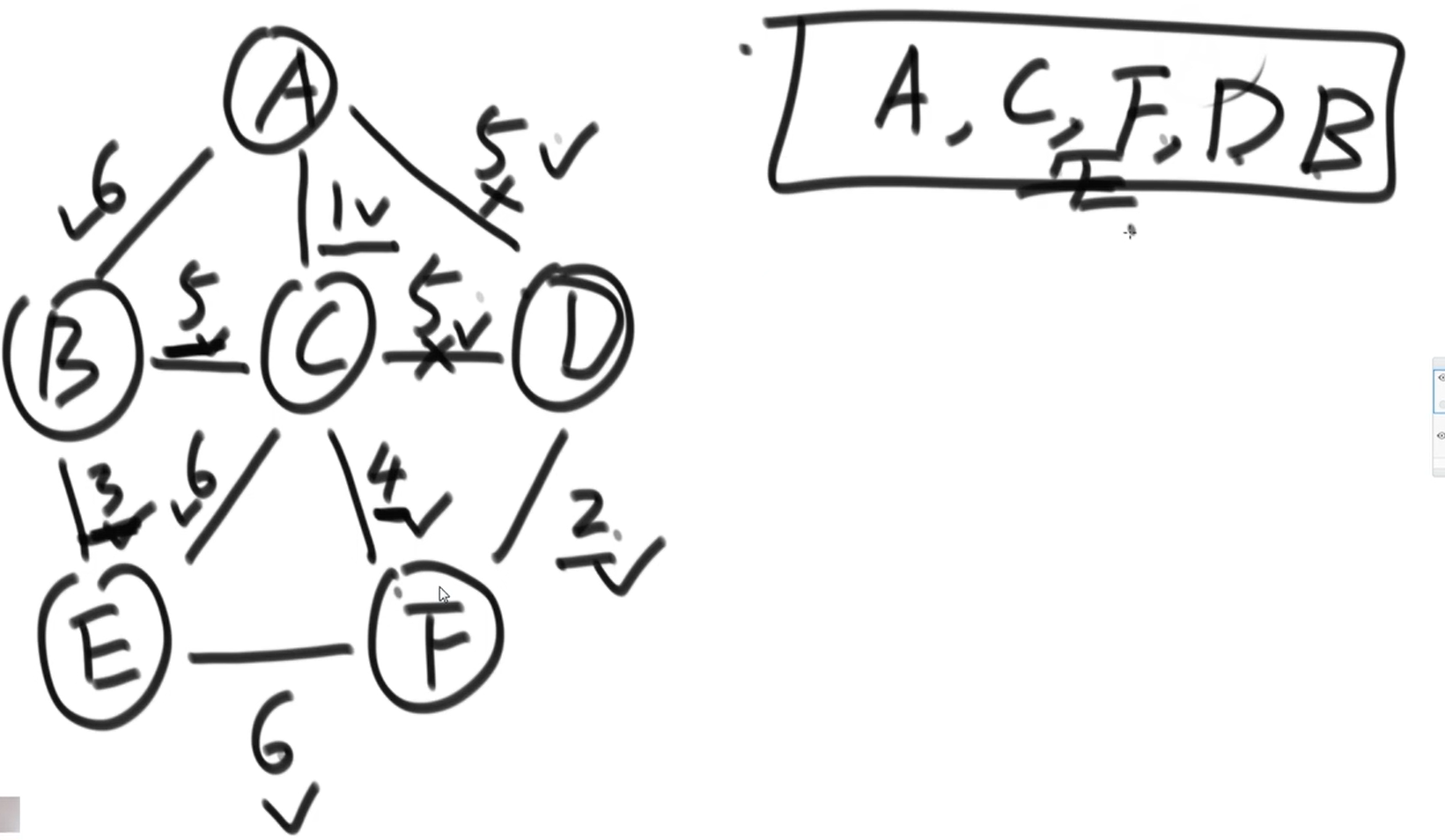
public class Prim {public Set<Edge> primMST(Graph graph) {PriorityQueue<Edge> queue = new PriorityQueue<>(Comparator.comparingInt(e -> e.weight));Set<Node> set = new HashSet<>();Set<Edge> result = new HashSet<>();//处理森林问题（有可能整个图不是全连通的）for (Node node : graph.nodes.values()) {if (!set.contains(node)) {set.add(node);//开始的点queue.addAll(node.edges);while (!queue.isEmpty()) {Edge edge = queue.poll();//弹出权值最小的边Node to = edge.to;//这条边指向的点if (!set.contains(to)) {//没包含过这个点，这条边可行set.add(to);result.add(edge);queue.addAll(to.edges);//解锁该点的其他边}}}}return result;}
}

最短路径–Dijkstra算法

适用于：不能有累加和为负数的环

规定了出发点，算出从该点出发，到每个点的最短距离

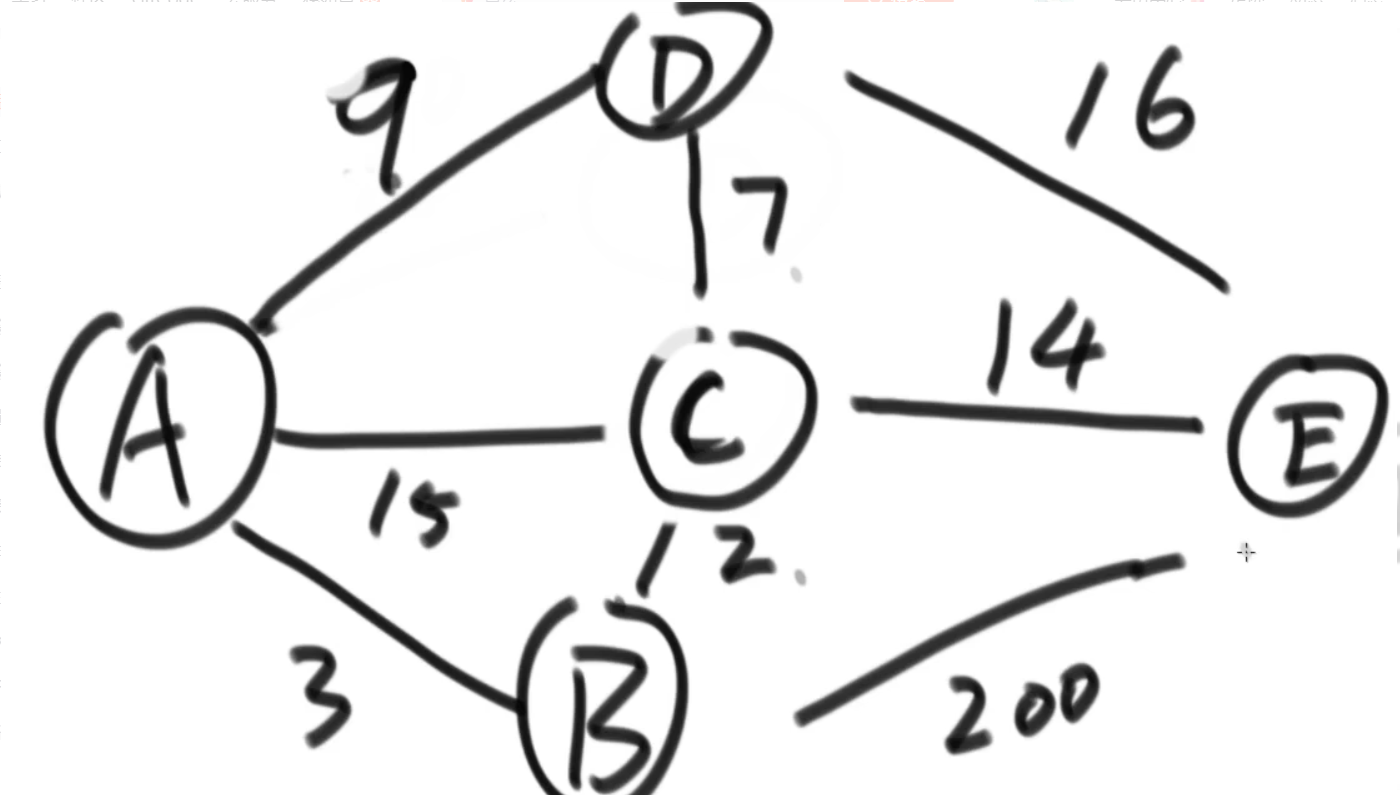
如：A–B–3、A–C–5、A–D–9、A–E–19

A	B	C	D	E
A	0	inf	inf	inf	inf

初始化一个表，从左到右依次取点，这个点之前锁死，以这个点为起点连成的路径若能使表格内数据更小，更新数据

代码：

public class Dijkstra {public Map<Node, Integer> dijkstra(Node node) {Map<Node, Integer> distanceMap = new HashMap<>();Set<Node> selectedNodes = new HashSet<>();distanceMap.put(node, 0);Node minNode = getMinDAndUN(distanceMap, selectedNodes);while (minNode != null) {Integer distance = distanceMap.get(minNode);for (Edge edge : minNode.edges) {Node toNode = edge.to;if (!distanceMap.containsKey(toNode)) {distanceMap.put(toNode, distance + edge.weight);} else {distanceMap.put(toNode, Math.min(distance + edge.weight, distanceMap.get(toNode)));}}selectedNodes.add(minNode);minNode = getMinDAndUN(distanceMap, selectedeNodes);}return distanceMap;}private Node getMinDAndUN(Map<Node, Integer> distanceMap, Set<Node> selectedNodes) {int minDistance = Integer.MAX_VALUE;Node result = null;for (Map.Entry<Node, Integer> entry : distanceMap.entrySet()) {Node node = entry.getKey();Integer distance = entry.getValue();if (!selectedNodes.contains(node) && minDistance > distance) {minDistance = distance;result = node;}}return result;}
}

可以用堆来优化，但是要自定义堆，不能使用系统自带的堆，因为在Dijkstra算法中加入的路径值会随着选用不同点为基点而变化，系统自带堆对这样的变化调整时间复杂度是o(N)的，所以需要自己手写堆

代码：

public static HashMap<Node, Integer> dijkstra2(Node head, int size) {NodeHeap nodeHeap = new NodeHeap(size);nodeHeap.addOrUpdateOrIgnore(head, 0);HashMap<Node, Integer> result = new HashMap<>();while (!nodeHeap.isEmpty()) {NodeRecord record = nodeHeap.pop();Node cur = record.node;int distance = record.distance;for (Edge edge : cur.edges) {nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance);}result.put(cur, distance);}return result;
}public static class NodeHeap {private Node[] nodes;private HashMap<Node, Integer> heapIndexMap;private HashMap<Node, Integer> distanceMap;private int size;public NodeHeap(int size) {nodes = new Node[size];heapIndexMap = new HashMap<>();distanceMap = new HashMap<>();this.size = 0;}public boolean isEmpty() {return size == 0;}public void addOrUpdateOrIgnore(Node node, int distance) {if (inHeap(node)) {distanceMap.put(node, Math.min(distanceMap.get(node), distance));insertHeapify(node, heapIndexMap.get(node));}if (!isEntered(node)) {nodes[size] = node;heapIndexMap.put(node, size);distanceMap.put(node, distance);insertHeapify(node, size++);}}public NodeRecord pop() {NodeRecord nodeRecord = new NodeRecord(nodes[0], distanceMap.get(nodes[0]));swap(0, size - 1);heapIndexMap.put(nodes[size - 1], -1);distanceMap.remove(nodes[size - 1]);nodes[size - 1] = null;heapify(0, --size);return nodeRecord;}private void insertHeapify(Node node, int index) {while (distanceMap.get(nodes[index]) < distanceMap.get(nodes[(index - 1) / 2])) {swap(index, (index - 1) / 2);index = (index - 1) / 2;}}private void heapify(int index, int size) {int left = index * 2 + 1;while (left < size) {int smallest = left + 1 < size && distanceMap.get(nodes[left + 1]) < distanceMap.get(nodes[left])? left + 1 : left;smallest = distanceMap.get(nodes[smallest]) < distanceMap.get(nodes[index]) ? smallest : index;if (smallest == index) {break;}swap(smallest, index);index = smallest;left = index * 2 + 1;}}private boolean isEntered(Node node) {return heapIndexMap.containsKey(node);}private boolean inHeap(Node node) {return isEntered(node) && heapIndexMap.get(node) != -1;}private void swap(int index1, int index2) {heapIndexMap.put(nodes[index1], index2);heapIndexMap.put(nodes[index2], index1);Node tmp = nodes[index1];nodes[index1] = nodes[index2];nodes[index2] = tmp;}
}

通过向前向量实现：

static void dijkstra(int n) {dist[1] = 0;for(int i = 1;i <= n;i++) {int ind = 0;//找一个点距离i最近的点，记录序号			for(int j = 1;j <= n;j++) {if(!vis[j] && (ind == 0 || dist[j] < dist[ind])) {ind = j;}}vis[ind] = true;//找到目前已知的能够到最短距离的点(且没有被调整过)for(int j = head[ind];j != 0;j = edge[j].next) {//通过目前知道距离最近的点，调整能够通过这个点到达的所有点，缩短距离。if(dist[edge[j].to] > dist[ind] + edge[j].w) {dist[edge[j].to] = dist[ind] + edge[j].w;path[edge[j].to] = ind;//记录路径}}}
}

前缀树

一个字符串类型的数组arr1，另一个字符串类型的数组类型arr2。

arr2中有哪些字符，是arr1中出现的？请打印。

arr2中有哪些字符，是作为arr1中某个字符串前缀出现的？请打印。

请打印arr2中出现次数最大的前缀。

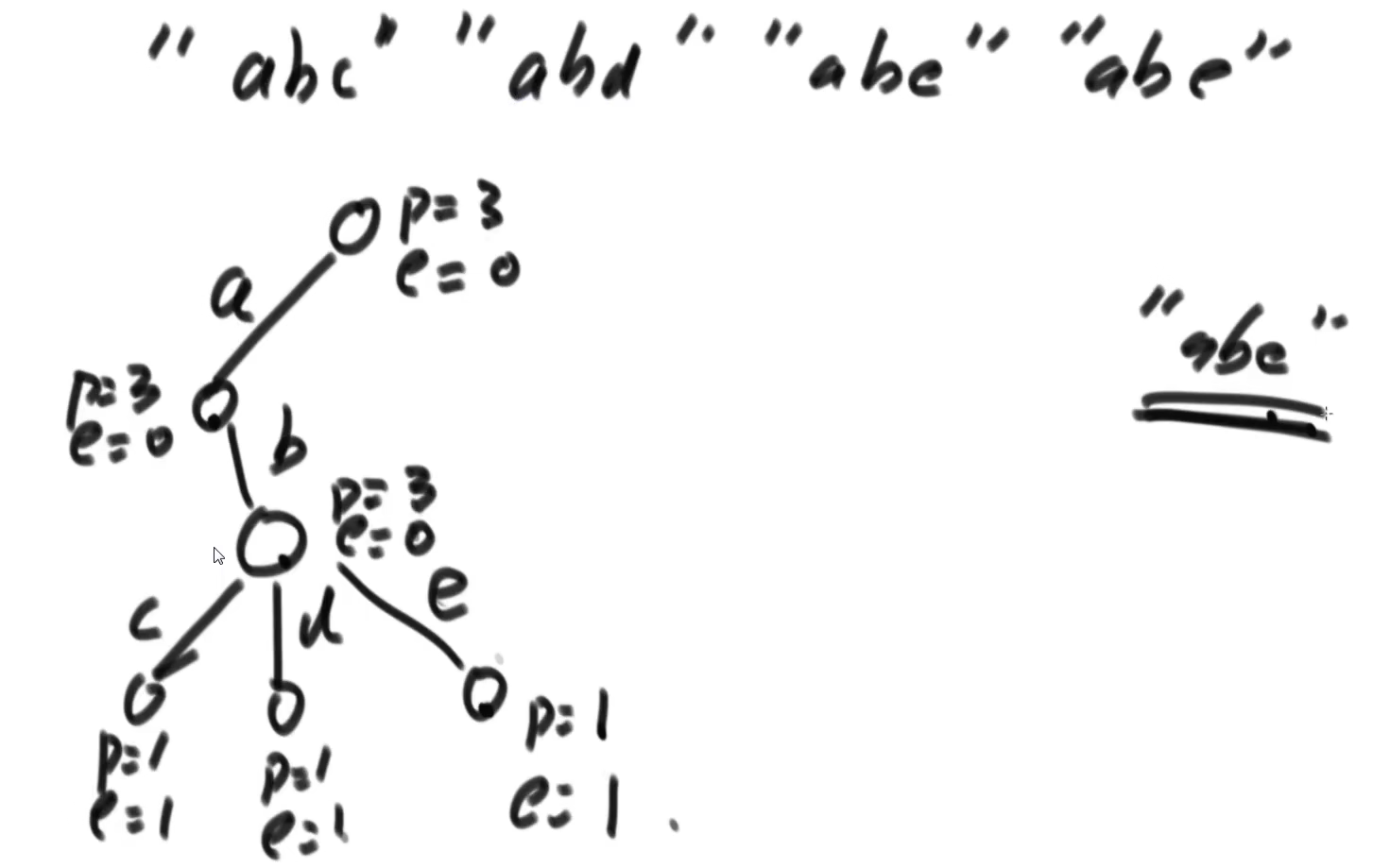
代码：

public class TrieTree {class TrieNode {public int pass;public int end;public TrieNode[] nexts;//如果不只是英文字母，可以用哈希表HashMap<char,node>public TrieNode() {pass = 0;end = 0;nexts = new TrieNode[26];}}private TrieNode root = new TrieNode();/*** 插入一个字符* @param str*/public void insert(String str) {if (str == null) {return;}char[] chars = str.toCharArray();TrieNode node = root;node.pass++;int index = 0;for (int i = 0; i < chars.length; i++) {index = chars[i] - 'a';if (node.nexts[index] == null) {node.nexts[index] = new TrieNode();}node = node.nexts[index];node.pass++;}node.end++;}/*** 寻找该字符加入了几个* @param str* @return*/public int search(String str){if (str == null) {return 0;}char[] chars = str.toCharArray();TrieNode node = root;int index = 0;for (int i = 0; i < chars.length; i++) {index = chars[i] - 'a';if (node.nexts[index] == null) {return 0;}node = node.nexts[index];}return node.end;}/*** 寻找前缀数量* @param pre* @return*/public int prefixNumber(String pre){if (pre == null) {return 0;}char[] chars = pre.toCharArray();TrieNode node = root;int index = 0;for (int i = 0; i < chars.length; i++) {index = chars[i] - 'a';if (node.nexts[index] == null) {return 0;}node = node.nexts[index];}return node.pass;}/*** 删除一个字符串* @param word*/public void delete(String word){if (search(word) != 0) {char[] chars = word.toCharArray();TrieNode node = root;node.pass--;int index = 0;for (int i = 0; i < chars.length; i++) {index = chars[i] - 'a';if(--node.nexts[index].pass == 0){node.nexts[index] = null;return;}node = node.nexts[index];}node.end--;}}
}

C++没有垃圾回收机制，node.nexts[index] = null;不能直接指null，c++还要遍历到底部手动析构

贪心

在某一个标准下，优先考虑最满足标准的样本，最后考虑最不满足标准的样本，最终得到
一个答案的算法，叫作贪心算法。
也就是说，不从整体最优上加以考虑，所做出的是在某种意义上的局部最优解。
局部最优-?-> 整体最优

贪心算法的在笔试时的解题套路：

实现一个不依靠贪心策略的解法X，可以用暴力的尝试
脑补出贪心策略A、贪心策略B、贪心策略C…
用解法X和对数器，去验证每一个贪心策略，用实验的方式得知哪个贪心策略正确
不要去纠结贪心策略的证明

常用技巧：

建立比较器排序
建立比较器来构造堆

贪心算法的难点，在于证明局部最优解的过程可以得到全局最优解。

会议室安排

一些项目要占用一个会议室宣讲，会议室不能同时容纳两个项目的宣讲。给你每一个项目开始的时间和结束的时间(给你一个数组，里面是一个个具体的项目)，你来安排宣讲的日程，要求会议室进行的宣讲的场次最多。返回这个最多的宣讲场次。

代码：

public class BestArrange {class Program {public int start;public int end;public Program(int start, int end) {this.start = start;this.end = end;}}public int bestArrange(Program[] programs, int start) {Arrays.sort(programs, Comparator.comparingInt(e -> e.end));int result = 0;for (int i = 0; i < programs.length; i++) {if (start <= programs[i].start) {result++;start = programs[i].end;}}return result;}
}

最小字典序的字符串拼接

给定任意个字符串，将它们拼接在一起，返回拼接之后字典序最小的字符串。

策略一：一个字符串在字典里排的越靠前，其字典序越小如：

abc < bck
b > apple

最朴素的想法：每个串进行排序，然后拼接例如

b < ba
bba < bab

很明显这个方案不对，bba是大于bab字典序的

另一个策略：a和b结合，比较b和a结合，谁小谁放前面

public class LowestString {public String lowestString(String[] strings) {if (strings == null || strings.length == 0) {return "";}Arrays.sort(strings, (s1,s2) -> (s1 + s2).compareTo(s2 + s1));StringBuilder res = new StringBuilder();for (int i = 0; i < strings.length; i++) {res.append(strings[i]);}return res.toString();}
}

尝试证明一下正确性：

比较一定是要有传递性的，如a<b、b<c，那a一定小于c

所以只需证：若ab<ba && bc<cb，则ac<ca

把字符串理解为K进制的数字

a拼b == a*m(b)+b，m(b)为Kb长度

所以有:

a * m(b) + b <= b * m(a) + a

b * m(c) + c <= c * m(b) + b

则有：

a * m(b) * c <= b * m(a) * c + a * c - b * c

b * m(c) * a + c * a - b * a <= c * m(b) * a

即：b * m(c) * a + c * a - b * a <= b * m(a) * c + a * c - b * c

进而：m(c) * a + c <= m(a) * c + a

即：a拼c < c拼a

即这种方法排序是有传递性的

接下来证明有效性

下面的序列字典序是递增的
[…,a,m1,m2,b,…]
[…,m1,a,m2,b,…]
[…,m1,m2,a,b,…]
[…,m1,m2,b,a,…]
然后用数学归纳法

可以看出贪心算法的验证是比较麻烦的，而且每个业务的证明都不一样，所以应该使用对数器验证

切金条–哈夫曼编码问题

题目：一块金条切成两半，是需要花费和长度数值一样的铜板的。

比如长度为20的金条，不管切成长度多大的两半，都要花费20个铜板。

一群人想整分整块金条，怎么分最省铜板?

例如，给定数组{10, 20, 30}，代表一共三个人，整块金条长度为10+20+30=60.
金条要分成10, 20, 30三个部分。如果先把长度60的金条分成10和50，花费60;
再把长度50的金条分成20和30，花费50; 一共花费110铜板。
但是如果先把长度60的金条分成30和30，花费60;再把长度30金条分成10和20,
花费30; 一共花费90铜板。
输入一个数组，返回分割的最小代价。

贪心策略：反向合并，每次合并最小的两块，最后总的价格最低。哈夫曼树。

代码：

public class LessMoney {public int lessMoney(int[] arr) {PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();for (int i = 0; i < arr.length; i++) {priorityQueue.add(arr[i]);}int res = 0;int cur;while (priorityQueue.size() > 1) {Integer i1 = priorityQueue.poll();Integer i2 = priorityQueue.poll();cur = i1 + i2;res += cur;priorityQueue.add(cur);}return res;}
}

投资项目

输入:
正数数组costs，正数数组profits，正数k，正数m
含义:
costs[i]表示i号项目的花费
profits[i]表示i号项目在扣除花费之后还能挣到的钱(利润)
k表示你只能串行的最多做k个项目
m表示你初始的资金
说明:
你每做完一个项目，马上获得的收益，可以支持你去做下一个项目。
输出:
你最后获得的最大钱数。

思路：

准备一个小顶堆(花费小的优先)、一个大顶堆(利润大的优先)
根据起始资金，去小根堆中找能够接的项目，将它们全部加入大根堆
从大根堆中选择一个利润最大项目做
然后获得新的资金后重复这个过程

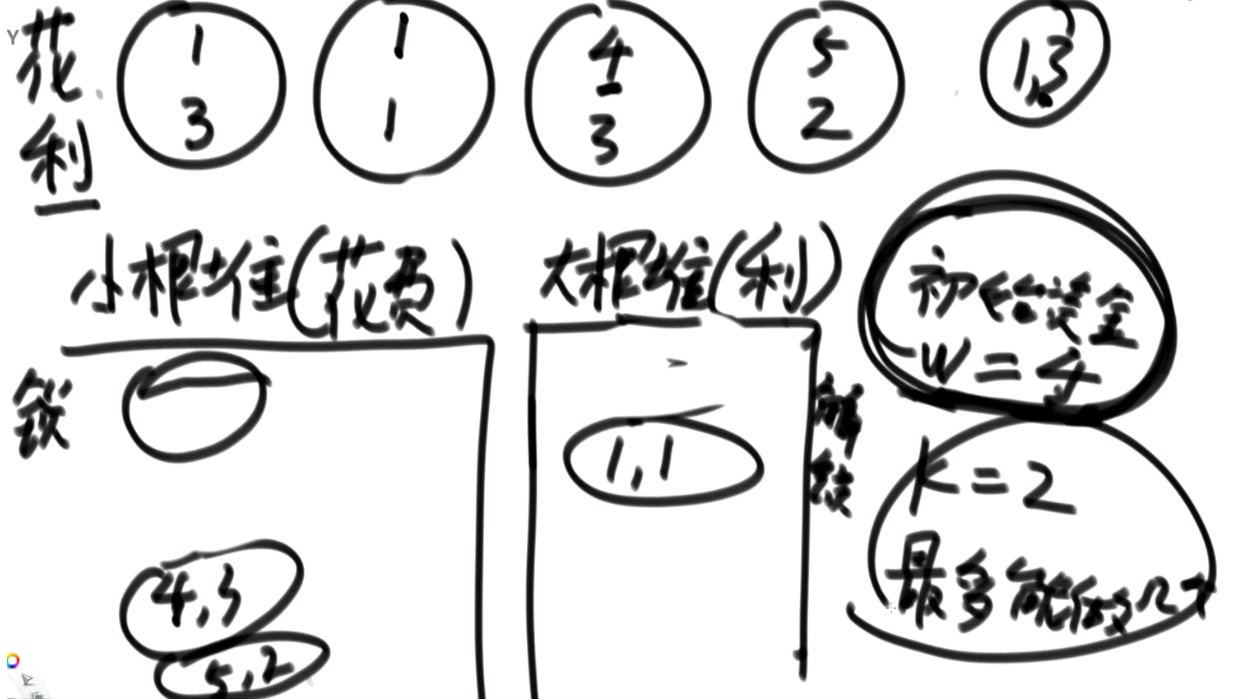
代码：

public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {PriorityQueue<Node> minQue = new PriorityQueue<>((Comparator.comparing(n -> n.capital)));PriorityQueue<Node> maxQue = new PriorityQueue<>((Comparator.comparing(n -> -n.profit)));for (int i = 0; i < profits.length; i++) {minQue.add(new Node(profits[i], capital[i]));}for (int i = 0; i < k; i++) {while (!minQue.isEmpty() && minQue.peek().capital <= w) {maxQue.add(minQue.poll());}if (maxQue.isEmpty()) {return w;}w += maxQue.poll().profit;}return w;}

随时获得中位数

一个数据流中，可以随时获得中位数

思路：准备一个大根堆放较小的一半，一个小根堆放较大的一半

每当有一个新的数字进入，马上和大根堆顶比较

若cur <= 大根堆堆顶，放入大根堆，否则加入小根堆

比较大根堆和小根堆大小，若 |size(大根堆) - size(小根堆)| > 2，则较大的那个弹出一个去较小的那个

代码：

public class MedianHolder {PriorityQueue<Integer> minHeap = new PriorityQueue<>();PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.comparingInt(i -> -i));public void addNumber(int num) {if (maxHeap.isEmpty() || num <= maxHeap.peek()) {maxHeap.add(num);} else {minHeap.add(num);}modifyTwoHeapsSize();}private void modifyTwoHeapsSize() {if (minHeap.size() - maxHeap.size() == 2) {maxHeap.add(minHeap.poll());}if (maxHeap.size() - minHeap.size() == 2) {minHeap.add(maxHeap.poll());}}public Integer getMedian() {int maxHeapSize = maxHeap.size();int minHeapSize = minHeap.size();if (maxHeapSize + minHeapSize == 0) {return null;}Integer maxHeapHead = maxHeap.peek();Integer minHeapHead = minHeap.peek();if ((minHeapSize + minHeapSize) / 2 == 0) {return (minHeapHead + maxHeapHead) / 2;}return maxHeapSize > minHeapSize ? maxHeapHead : minHeapHead;}
}

暴力递归

暴力递归就是尝试，是动态规划的基础

把问题转化为规模缩小了的同类问题的子问题
有明确的不需要继续进行递归的条件**(base case)**
有当得到了子问题的结果之后的决策过程
不记录每一个子问题的解

在这里之所以是暴力，是因为每一次不记录子问题的解，如果每一次记录子问题的解，那么就是动态规划。

汉诺塔问题

大圆盘不能放在小圆盘上面，给定层数N，打印出层数

public class Hanoi {public void hanoi(int n) {fun(n, "左", "中", "右");}private void fun(int i, String from, String to, String other) {if (i == 1) {System.out.println("move 1 from " + from + " to " + to);} else {fun(i - 1, from, other, to);System.out.println("move " + i + " from " + from + " to " + to);fun(i - 1, other, to, from);}}
}

字符串的全部子序列

分支问题 – 从左到右

打印一个字符串的全部子序列，包括空字符串

public class Subsequence {public void printAllSubsequence(String srt) {char[] chars = srt.toCharArray();process(chars, 0);}private void process(char[] chars, int index) {if (index == chars.length) {System.out.println(chars);return;}process(chars, index + 1);char temp = chars[index];chars[index] = 0;process(chars, index + 1);chars[index] = temp;}
}

打印一个字符串的全部排列

分支问题 – 从左到右

public class Permutations {@Testpublic void test() {List<String> list = printAllPermutations("abca");System.out.println(list.toString());}public List<String> printAllPermutations(String str) {List<String> res = new ArrayList<>();if (str == null || str.length() == 0) {return res;}char[] chars = str.toCharArray();process(chars, 0, res);return res;}private void process(char[] chars, int index, List<String> res) {if (index == chars.length) {res.add(String.valueOf(chars));}//去除重复项boolean[] visit = new boolean[26];for (int i = index; i < chars.length; i++) {if (!visit[chars[i] - 'a']) {visit[chars[i] - 'a'] = true;swap(chars, i, index);process(chars, index + 1, res);swap(chars, i, index);}}}private void swap(char[] chars, int i, int j) {char temp = chars[i];chars[i] = chars[j];chars[j] = temp;}
}

拿牌游戏

分支问题

给定一个整型数组arr，代表数值不同的纸牌排成一条线。

玩家A和玩家B依次拿走每张纸牌，规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A和玩家B都绝顶聪明。

请返回最后获胜者的分数。

思路：f是先手函数，表示在L到R上先手的情况获得的分数。当在这个范围上先手拿牌时，只剩下一张牌的情况就直接返回这一张牌。
s是后手函数，表示在L到R上后手的情况获得的分数。当在这个范围上后手拿牌时，因为只剩下一张牌，所以后手拿牌的得分是0。
先手函数会在arr左右选一张牌，最后结果是对自己最好的，并且下一次选牌将变为后手；
后手函数选牌时将变为先手，并且后手选牌一定会缩小1个范围，可能是左或右；由于先手足够聪明，所以后手函数只能获得缩小后的范围中【先手去拿的较小得分】(后手变先手)，相当于一切在先手函数的计算当中。

public class CardsInLine {@Testpublic void test() {System.out.println(win(new int[]{1, 2, 100, 4}));}public int win(int[] arr) {if (arr == null || arr.length == 0) {return 0;}return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));}private int f(int[] arr, int l, int r) {if (l == r) {return arr[l];}return Math.max(arr[l] + s(arr, l + 1, r), arr[r] + s(arr, l, r - 1));}private int s(int[] arr, int l, int r) {if (l == r) {return 0;}return Math.min(f(arr, l + 1, r), f(arr, l, r - 1));}
}

反转一个栈

给你一个栈，请你逆序这个栈，不能申请额外的数据结构，只能使用递归函数。如何实现?

public class ReverseStack {public void reverse(Stack<Integer> stack) {if (stack.isEmpty()) {return;}int i = f(stack);reverse(stack);stack.push(i);}public int f(Stack<Integer> stack) {int result = stack.pop();if (stack.isEmpty()) {return result;} else {int last = f(stack);stack.push(result);return last;}}
}

数字转化字符串

分支问题 – 从左到右

规定1和A对应、2和B对应、3和C对应…

那么一个数字字符串比如"111"，就可以转化为"AAA"、“KA"和"AK”。

给定一个只有数字字符组成的字符串str，返回有多少种转化结果。

思路：

如果当前位置为0，则不能转换；
如果当前位置为1，则可以选择自己单独转换，或者与后面一个数结合一起转换；
如果当前位置为2，则可以选择自己单独转换，或者下一位不超过6的情况，可以一起结合转换；
如果当前位置大于等于3，只能单独转换。
如果当前位置已经到达字符串末尾，则已经形成一种转换结果。

public class ConvertNum {@Testpublic void test() {System.out.println(number("12314545"));}public int number(String str) {if (str == null || str.length() == 0) {return 0;}return process(str.toCharArray(), 0);}private int process(char[] chars, int i) {if (i == chars.length) {return 1;}if (chars[i] == '0') {return 0;}if (chars[i] == '1') {int res = process(chars, i + 1);if (i + 1 < chars.length) {res += process(chars, i + 2);}return res;}if (chars[i] == '2') {int res = process(chars, i + 1);if (i + 1 < chars.length && (chars[i + 1] >= '0' && chars[i + 1] <= '6')) {res += process(chars, i + 2);}return res;}return process(chars, i + 1);}
}

最大货物问题

给定两个长度都为N的数组weights和values，weights[i]和values[i]分别代表i号物品的重量和价值。

给定一个正数bag，表示一个载重bag的袋子，你装的物品不能超过这个重量。

返回你能装下最多的价值是多少？

public class Knapsack {@Testpublic void test() {System.out.println(maxValue1(new int[]{2, 1, 3}, new int[]{4, 3, 6}, 4));}public static int maxValue1(int[] weights, int[] values, int bag) {return process2(weights, values, 0, 0,0, bag);}private static int process1(int[] weights, int[] values, int i, int alreadyWeight, int bag) {if (alreadyWeight > bag) {return Integer.MIN_VALUE;}if (i == weights.length) {return 0;}return Math.max(process1(weights, values, i + 1, alreadyWeight, bag),values[i] + process1(weights, values, i + 1, alreadyWeight + weights[i], bag));}private static int process2(int[] weights, int[] values, int i, int alreadyWeight,int alreadyValue, int bag) {if (alreadyWeight > bag) {return 0;}if (i == values.length) {return alreadyValue;}return Math.max(process2(weights, values, i + 1, alreadyWeight, alreadyValue, bag),process2(weights, values, i + 1, alreadyWeight + weights[i], alreadyValue + values[i], bag));}
}

可以有很多种试法，无非就是尝试所有可能，不符合的可能屏除了而已，尝试方法中，参数越少越好

N皇后

在N*N的棋盘上要摆N个皇后，要求任何两个皇后不同行、不同列，也不在同一条斜线上。

给定一个整数N，返回N皇后的摆法有多少种。

如：
- n=1，返回1。
- n=2或3，2皇后和3皇后问题无论怎么摆都不行，返回0。
- n=8，返回92。

方法一：

public class Queen {@Testpublic void test() {System.out.println(num(8));}public int num(int n) {if (n < 1) {return 0;}int[] record = new int[n];return process1(record, 0, n);}private int process1(int[] record, int i, int n) {if (i == n) {return 1;}int res = 0;for (int j = 0; j < record.length; j++) {if (isValid(record, i, j)) {record[i] = j;res += process1(record, i + 1, n);}}return res;}private boolean isValid(int[] record, int i, int j) {for (int k = 0; k < i; k++) {if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {return false;}}return true;}
}

方法二：常数优化、位运算加速，加速了检查某个位置的合法性

将皇后所放的列的限制改为实用整数位进行标志，左斜线限制与右斜线限制也使用整数位进行标志，准备一个N个位的二进制数limit，用于确定位限制中的有效范围。

当前在第0行，想要在某一列放皇后，放入皇后之后，对应列限制的位改为1，代表这里要放皇后；
那么对应就会生成下一行的左斜线与右斜线限制，将当前行放入皇后的列限制左移1位就是下一行的左斜线限制，同理右移1位就是下一行的右斜线限制。
进入第1行的时候，尝试在可以放皇后的列放皇后，先将列限制、左右斜线限制的位通过与运算并起来，成为总限制，将总线制再取反和limit相与（忽略超过N的高位干扰），总线制为1的位在当前行才能放皇后，为0的位置则不能放皇后。
对处理过后的总线制，其每一个为1的位代表可以放皇后，依次取出每一位的1，进行遍历尝试。这里需要用到每次取出最右侧的1。t = a & (~a + 1)
当前行放皇后的位置确定之后，更新占用的列限制(或运算)；对应的左右斜线限制，需要在上一行的左右斜线限制的当前列位置变为1(或运算)，然后继续左移和右移，得到新的对于下一行的左右斜线限制。
右移时需要注意使用无符号右移，以免出现符号位被移入的情况。

代码：

public class Queen {@Testpublic void test() {System.out.println(num2(8));}/*** 常数项优化** @param n* @return*/public int num2(int n) {//一个int是四个字节既32bit，超过这个范围计算不了，可以用long类型if (n < 1 || n > 32) {return 0;}// 如8皇后问题，生成：0000 0000 1111 1111int upperLim = n == 32 ? -1 : (1 << n) - 1;return process2(upperLim, 0, 0, 0);}/*** @param upperLim* @param colLim      列限制* @param leftDiaLim  下一行左对角线限制* @param rightDiaLim 下一行右对角线限制* @return*/private int process2(int upperLim, int colLim, int leftDiaLim, int rightDiaLim) {if (colLim == upperLim) {return 1;}//判断哪些位置还可以放//如：colLim：00000001//leftDiaLim：00000010//rightDiaLim：00000000//(~(colLim | leftDiaLim | rightDiaLim)之后是11111100,1就是还可以放的位置//与upperLim与是为了把高位变为0，就是11111100之前的24位变为0int pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim));int mostRightOne = 0;int res = 0;while (pos != 0) {//取出最右位上的1mostRightOne = pos & (~pos + 1);pos = pos - mostRightOne;res += process2(upperLim, colLim | mostRightOne,(leftDiaLim | mostRightOne) << 1,(rightDiaLim | mostRightOne) >>> 1);}return res;}
}