文章目录
- 前言
- 一、树
- 1.1 树的概念
- 1.2 树的相关概念
- 1.3 树的表示
- 1.4 树的用途
- 二、二叉树
- 2.1 二叉树的概念
- 2.2 两种特殊的二叉树
- 2.3 二叉树的性质
- 2.4 二叉树的存储方式
- 总结
前言
树是一种让程序员们既爱又恨的数据结构。它就像是一棵大树,让你可以轻松地摘取其中的果实,但也让你不得不面对它茂密的枝叶和复杂的根系。如果你想要在编程领域中成为一名大师,那么你必须要学会如何在这片浓密的树林中游刃有余。所以,让我们开始探索这个神奇的世界吧!
一、树
1.1 树的概念
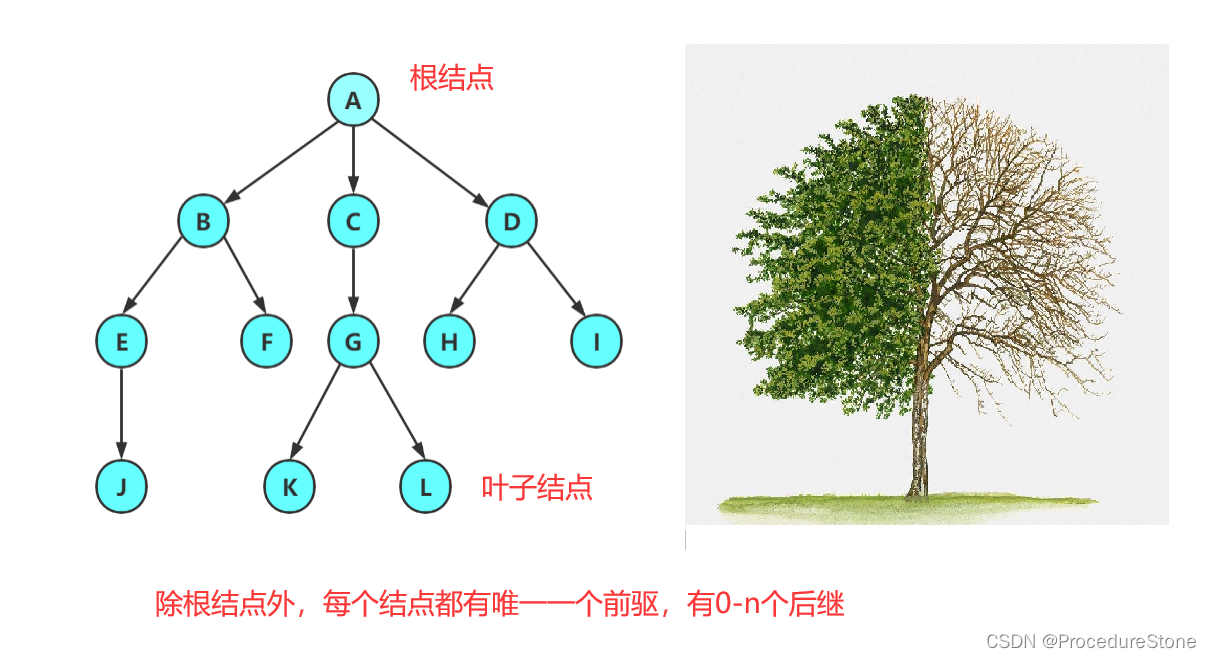
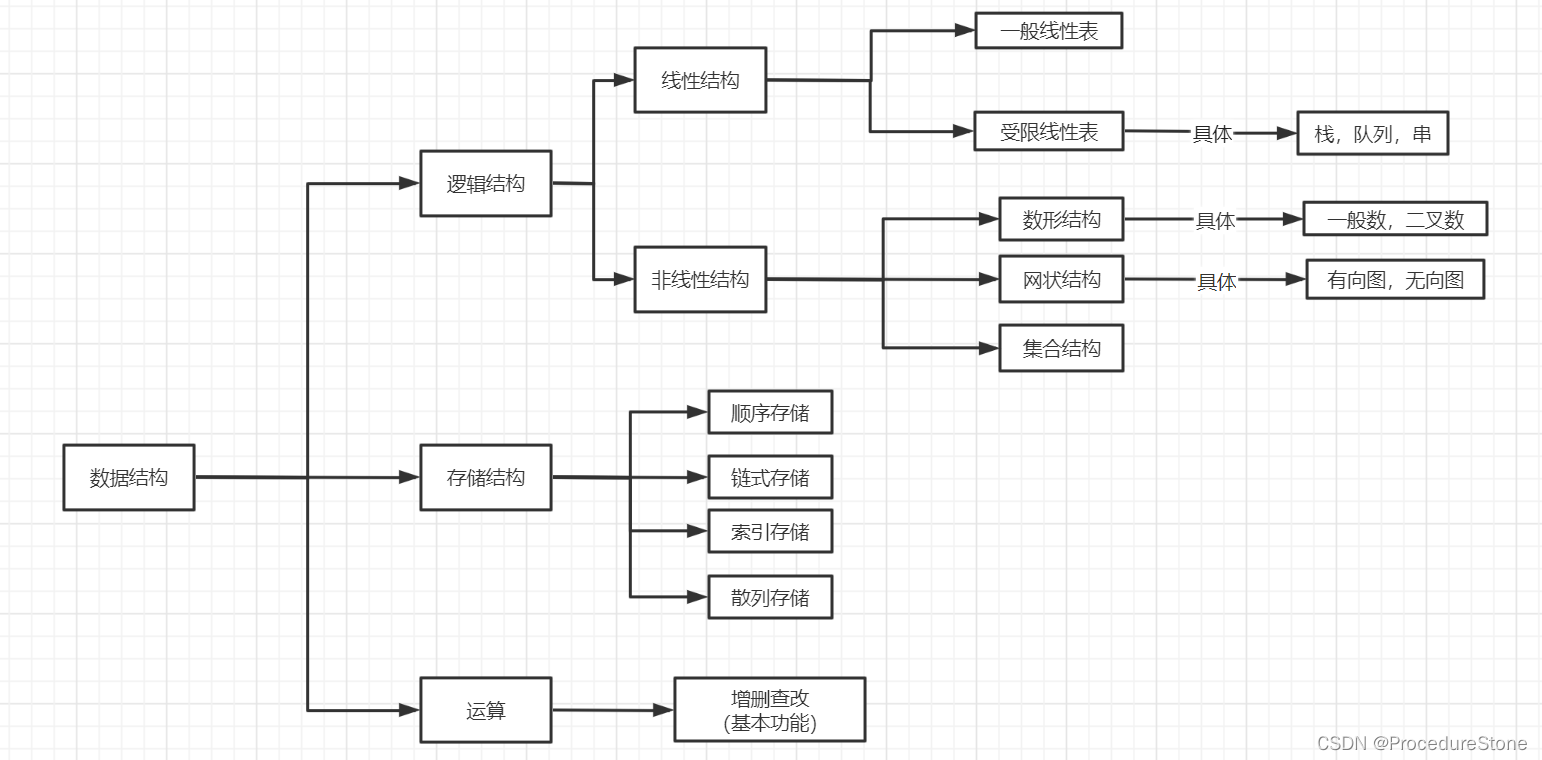
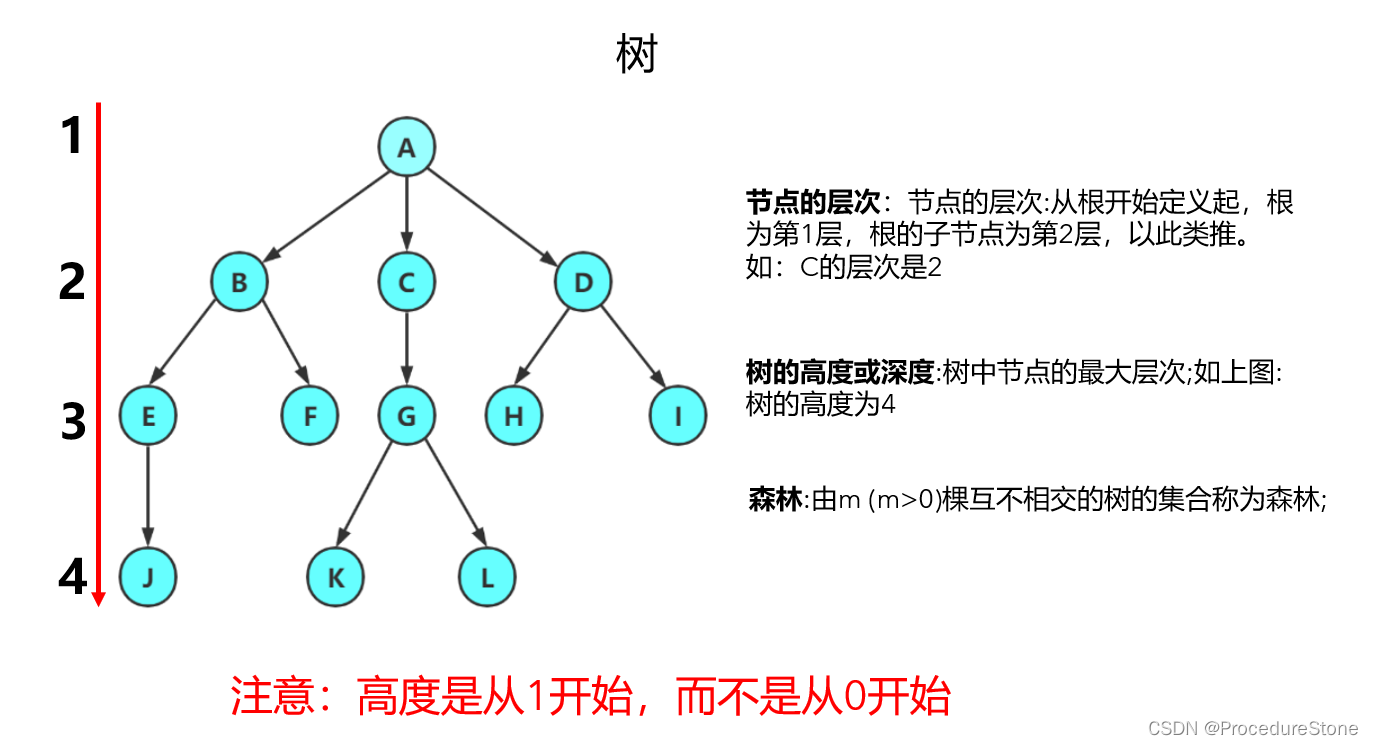
树的概念:树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
1.2 树的相关概念
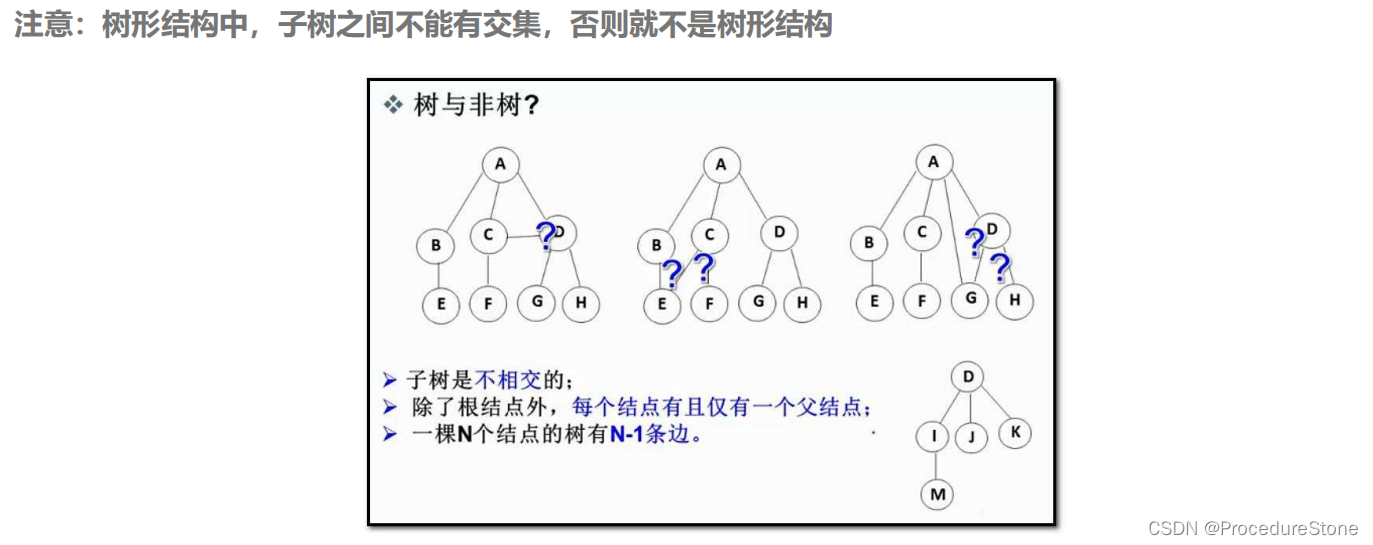
为了方便之后对树的学习,以下概念需要理解并记忆
- 节点
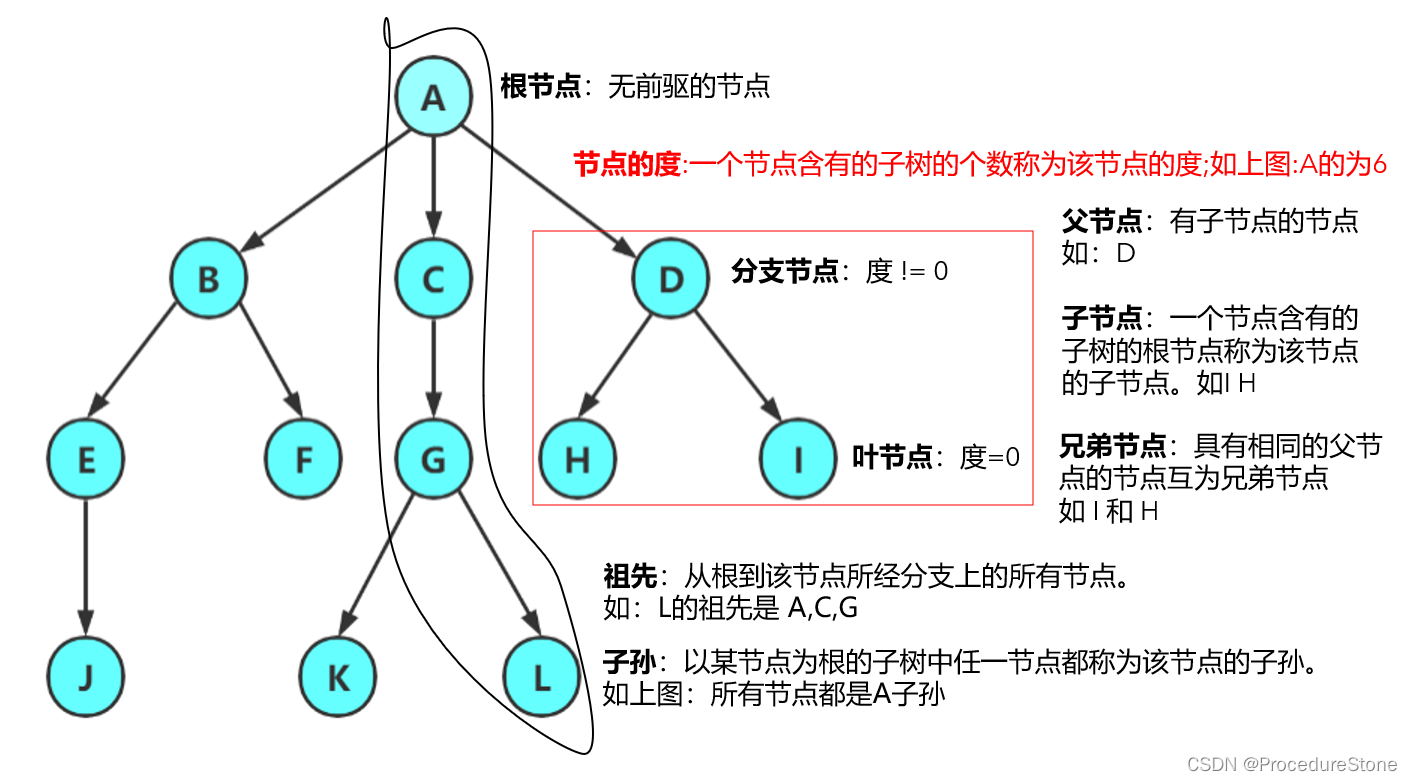
- 树
1.3 树的表示
在了解了树的定义及其相关概念后,我想你现在最好奇,该如何表示树呢?,有一位程序员大佬给出了其结构体。
typedef int DataType;
typedef struct TreeNode
{
struct TreeNode* FirstChild; // 第一个孩子结点
struct TreeNode* NextBrother; // 指向其下一个兄弟结点
DataType data; // 结点中的数据域
}TreeNode;
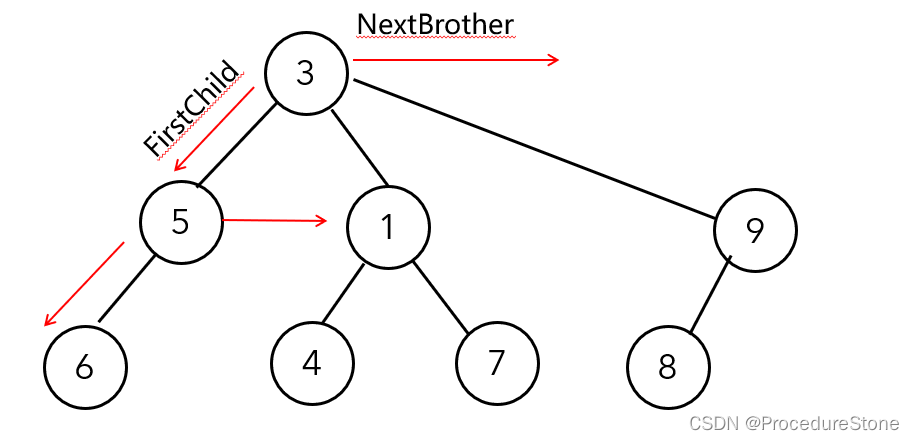
通过FirstChild和NextBrother可以遍历到每一个节点
1.4 树的用途
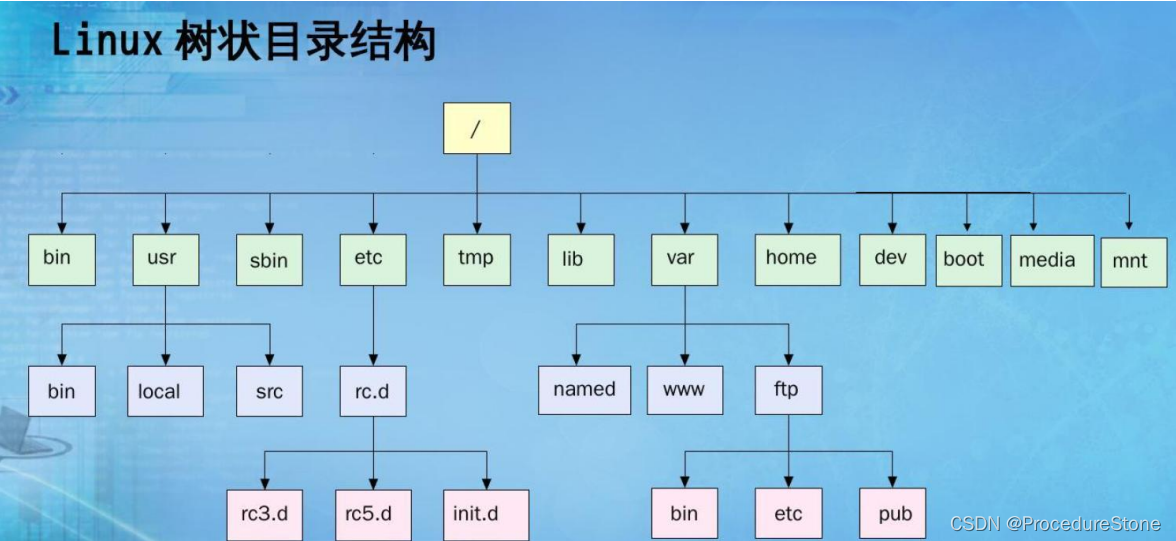
根据树的结构,很容易想到树的一种用途:文件管理
树这种数据结构有以下几个常见的用处:
-
组织数据:树可以用来组织层次化的数据,例如文件系统、目录结构、XML/HTML文档等。这些数据可以被看作是树形结构,每个节点表示一个文件/目录/标签,子节点表示该节点下的子文件/子目录/子标签。
-
搜索和排序:二叉搜索树是一种基于树的数据结构,可以用来实现快速的搜索和排序。在二叉搜索树中,每个节点的值都大于其左子节点的值,小于其右子节点的值,因此可以用二分查找的方法来快速地查找数据。
-
算法设计:树是许多算法的基础,例如图遍历、最短路径、最小生成树等。通过对树的遍历和操作,可以解决许多复杂的问题。
-
数据压缩:霍夫曼树是一种基于树的数据结构,可以用来实现数据的压缩。在霍夫曼树中,每个叶子节点表示一个字符,其编码是从根节点到该节点的路径上的0和1的序列,根据字符在文本中出现的频率构建霍夫曼树,可以得到一种高效的压缩方式。
总之,树这种数据结构在计算机科学中应用广泛,是许多算法和数据结构的基础。
二、二叉树
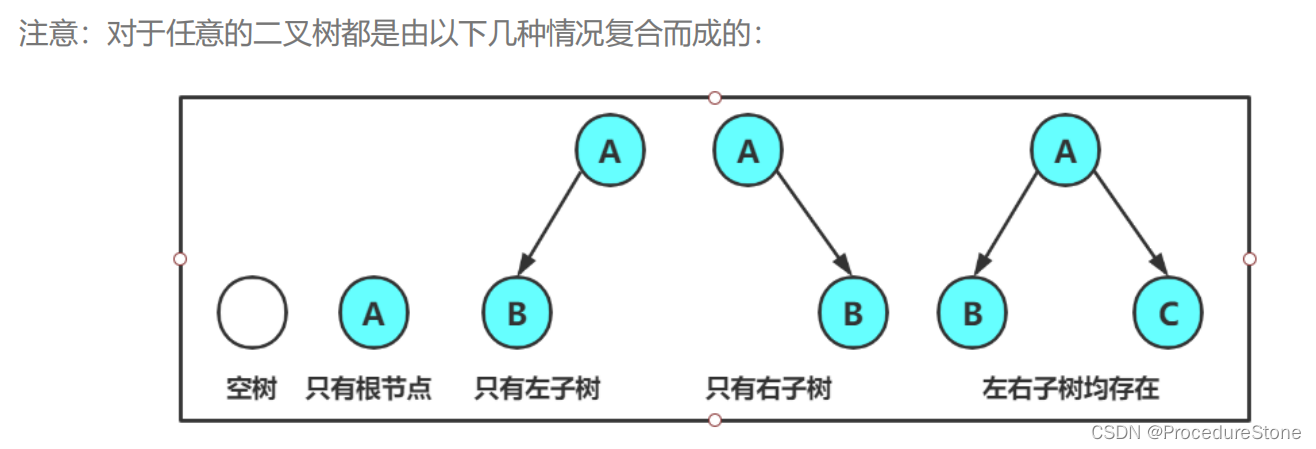
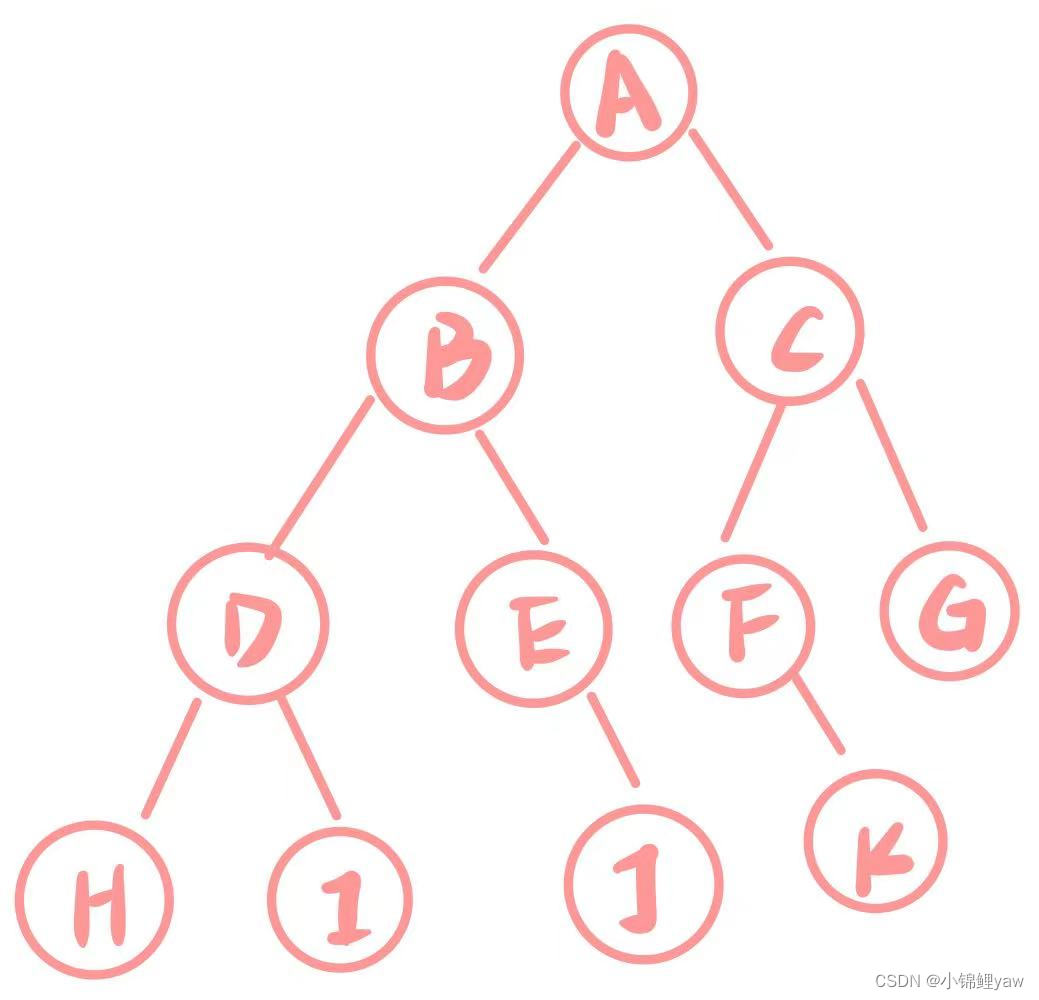
2.1 二叉树的概念
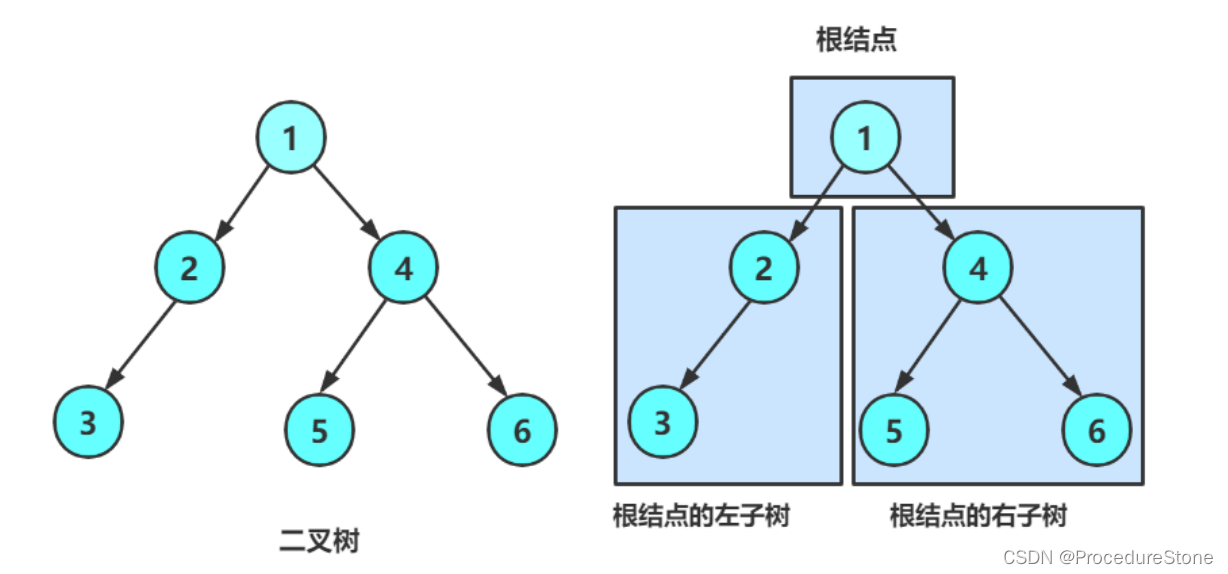
二叉树是一种特殊的树形结构,
- 每个节点最多只有两个子节点,分别被称为左子节点和右子节点。
- 左子树和右子树都是二叉树。
- 二叉树可以为空。
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
2.2 两种特殊的二叉树
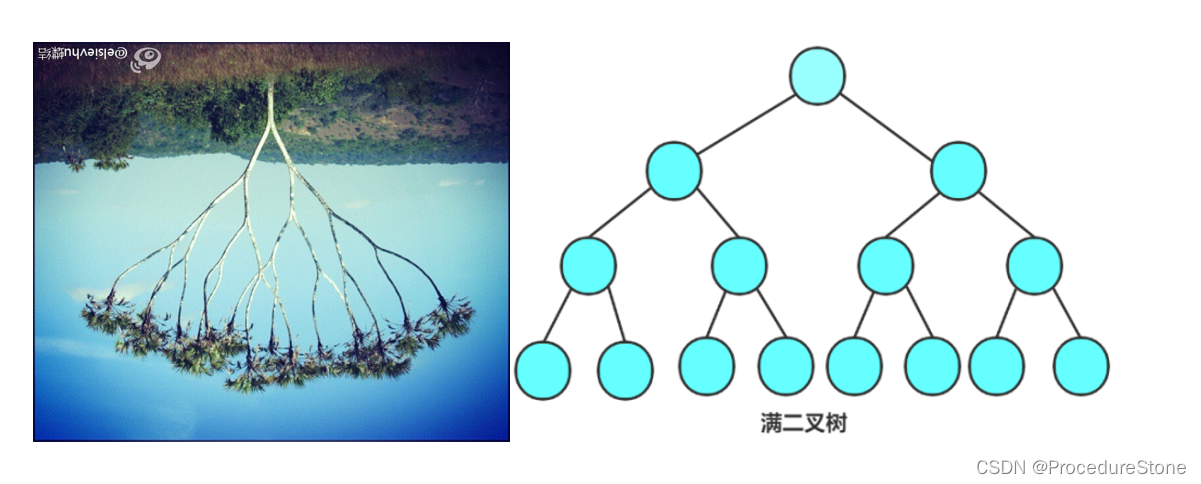
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
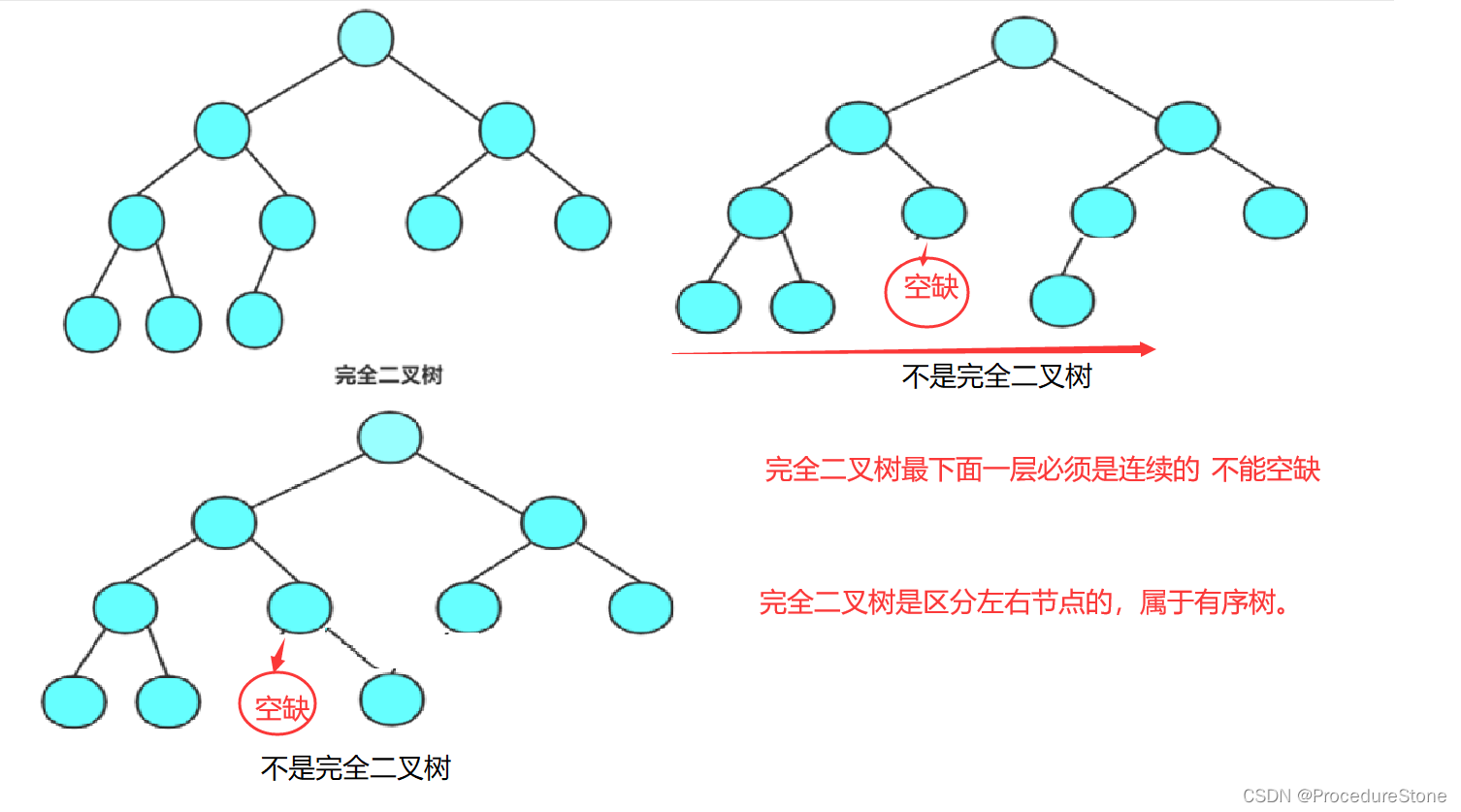
完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.3 二叉树的性质
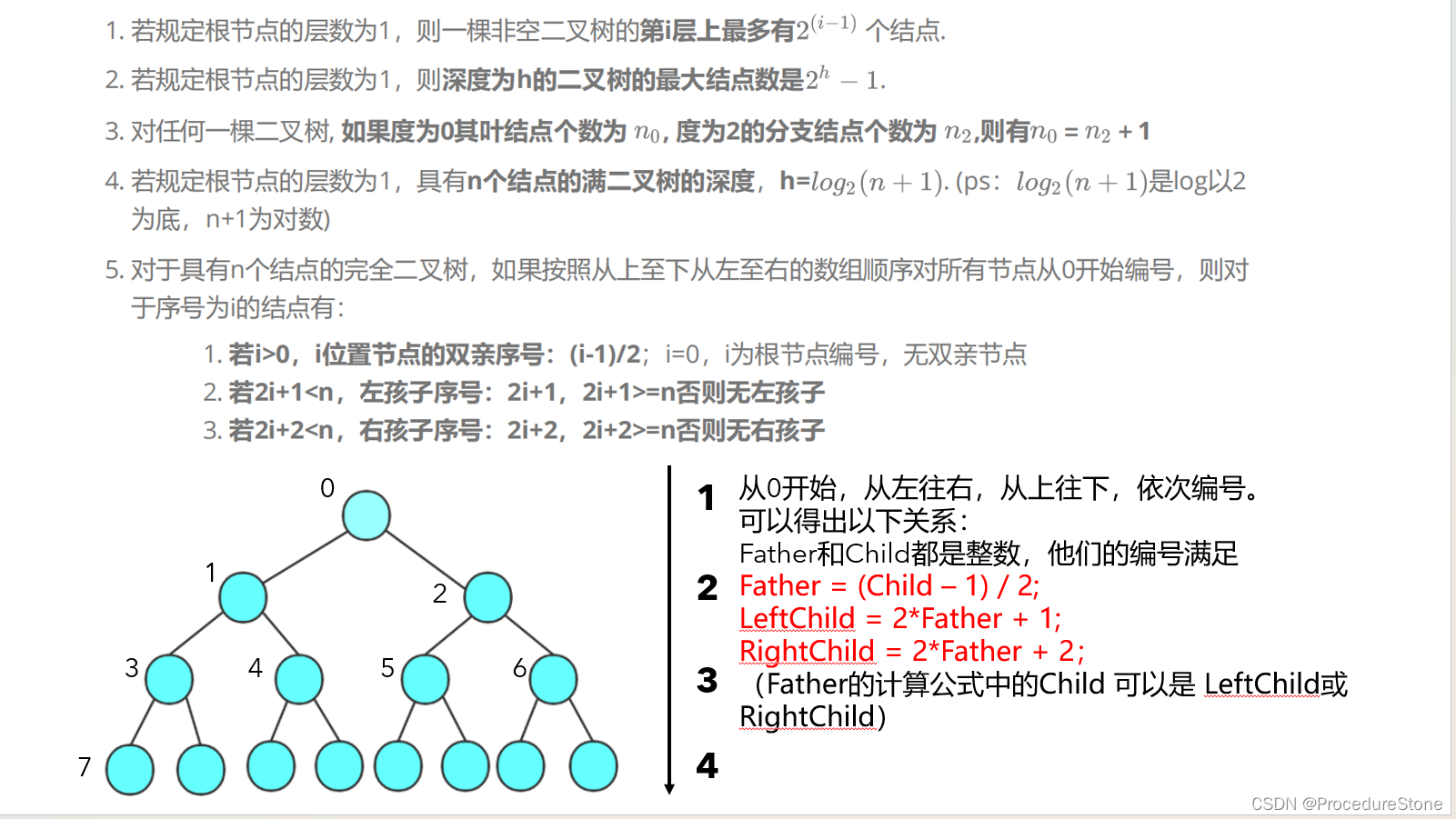
2.4 二叉树的存储方式
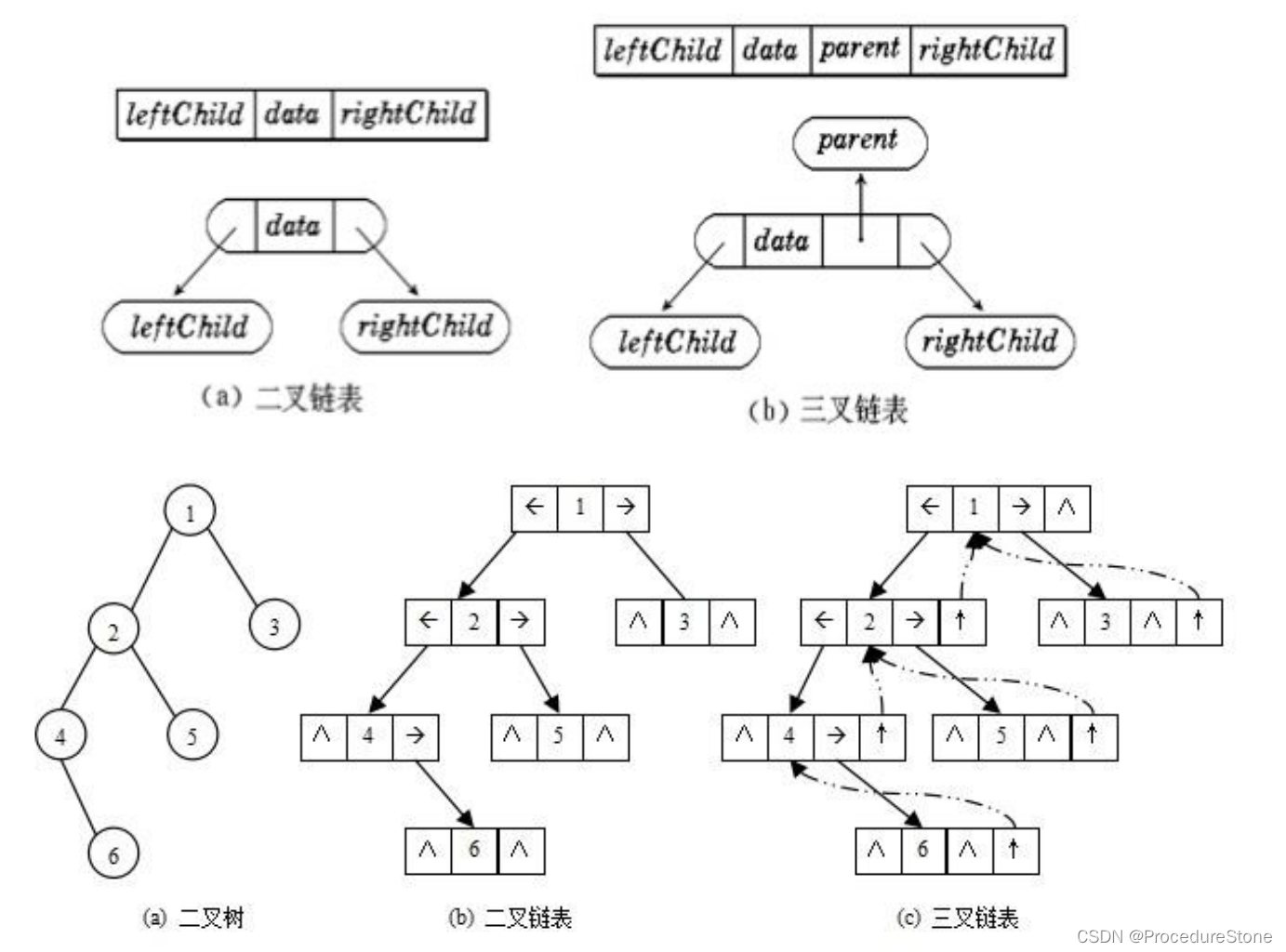
二叉树的存储方式:顺序存储和链式存储
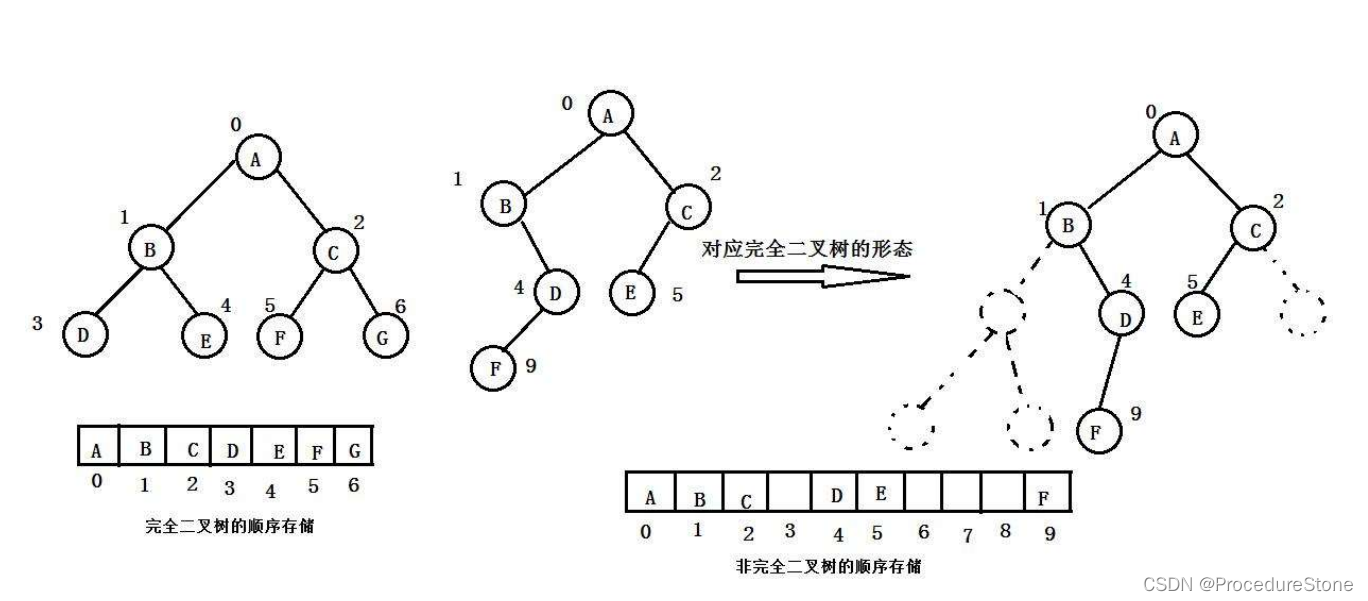
顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
注意:这里的堆指的是一种数据结构,而不是指内存的某一区域
链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链。
总结
树是一种非常重要的数据结构,它可以帮助我们处理许多复杂的问题。
感谢您阅读本文。如果您觉得这篇文章对您有所帮助,不妨给我点个赞,这将是对我最大的鼓励。同时,如果您对本文还有任何疑问或建议,欢迎在评论区留言,我会尽力回答和改进。谢谢!