2.3二叉树的存储

// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}

1.手动快速创建一棵简单的二叉树

 

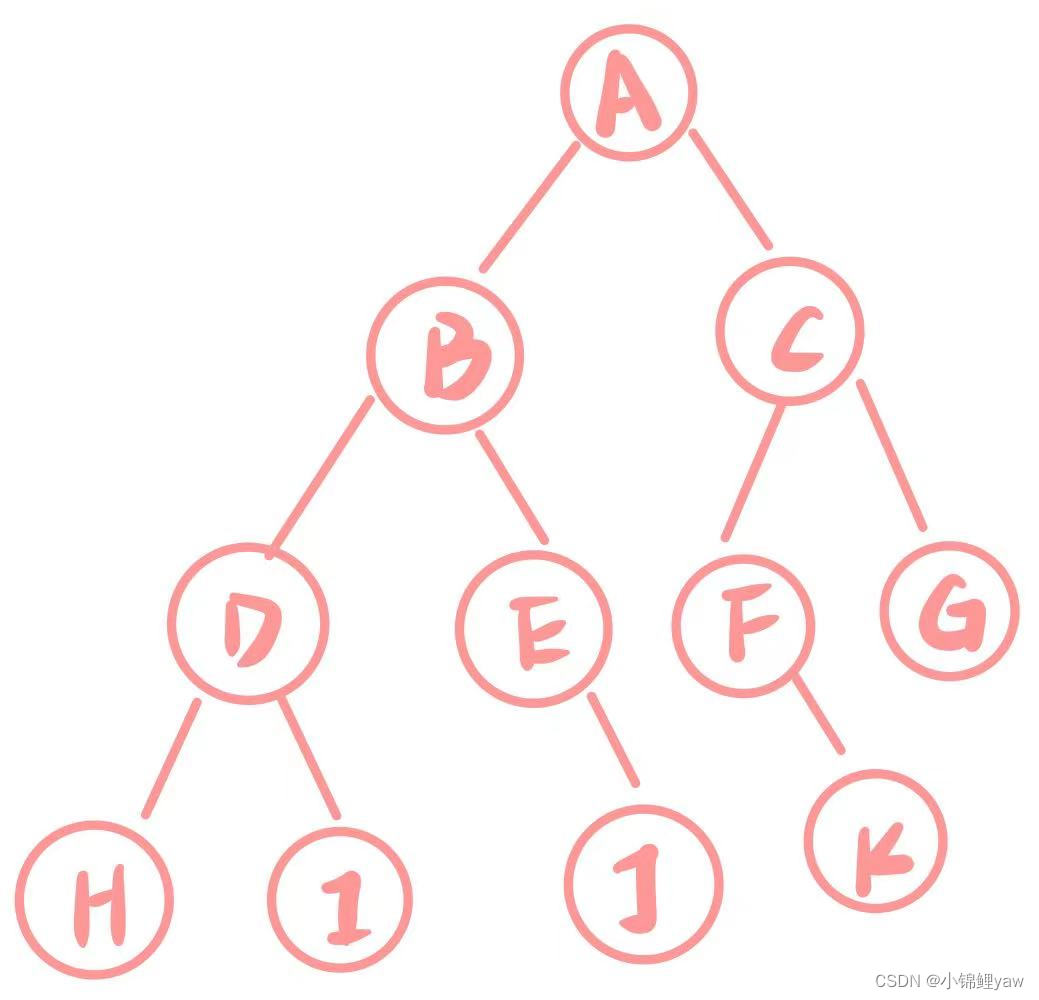
public Node TreeBuild(){Node node1 = new Node('A');Node node2 = new Node('B');Node node3 = new Node('C');Node node4 = new Node('D');Node node5 = new Node('E');Node node6 = new Node('F');Node node7 = new Node('G');Node node8 = new Node('H');Node node9 = new Node('I');Node node10 = new Node('J');Node node11 = new Node('K');node1.left = node2;node1.right = node3;node2.left = node4;node2.right = node5;node3.left = node6;node3.right = node7;node4.left = node8;node4.right = node9;node5.right = node10;node6.right = node11;return node1;}

·   //前序遍历public void preOrder(Node root){if(root == null){return ;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}//中序遍历public void inOrder(Node root){if(root == null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}//后序遍历public void postOrder(Node root){if(root == null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}

    //层序遍历public List<List<Character>> levelOrder(Node root){//创建一个二维数组保存每一层的元素List<List<Character>> list = new ArrayList<>();if(root == null){return list;}//临时队列Deque<Node> deque = new LinkedList<>();//头节点放入队列deque.offer(root);//队列非空进循环while(!deque.isEmpty()){int size = deque.size();List<Character> curList = new ArrayList<>();for (int i = 0; i < size; i++){Node x = deque.pop();//左子树不为空，左子树入队列if(x.left != null){deque.offer(x.left);}//右子树不为空，右子树入队列if(x.right != null){deque.offer(x.right);}//出栈的元素值存放在临时数组里curList.add(x.val);}//出循环将临时数组加入二维数组list.add(curList);}return list;}

4.获取树中节点的个数

    public int size(Node root){if(root == null){return 0;}return 1 + size(root.left) + size(root.right);}

5.获取叶子节点的个数

    // 获取叶子节点的个数int getLeafNodeCount(Node root){if(root == null){return 0;}if(root.left == null && root.right == null){return 1;}return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);}

6.获取第K层节点的个数

    // 获取第K层节点的个数int getKLevelNodeCount(Node root,int k){if(root == null || k <= 0){return 0;}if(k == 1){return 1;}return getKLevelNodeCount(root.left,k-1) + getKLevelNodeCount(root.right,k-1);}

7.获取二叉树的高度

    // 获取二叉树的高度int getHeight(Node root){if(root == null){return 0;}return 1 + Math.max(getHeight(root.left),getHeight(root.right));}

8.检测值为value的元素是否存在

    // 检测值为value的元素是否存在public boolean find(Node root, int val){if(root == null){return false;}if(root.val == val){return true;}return find(root.left,val) || find(root.right,val);}

9.判断一棵树是不是完全二叉树

    // 判断一棵树是不是完全二叉树boolean isCompleteTree(Node root){if(root == null){return true;}//队列为空出循环，两个阶段//1.所有都是度为2的节点//2.碰到第一个度为1的节点，右节点直接false,左节点进入第二阶段//碰到第一个度为0的节点，进入第二阶段//3。第二阶段，都是叶子节点，如果有不是叶子节点，直接falseDeque<Node> deque = new LinkedList<>();deque.offer(root);boolean flag = true;while(!deque.isEmpty()){if(flag){Node x = deque.poll();if(x.left != null && x.right != null){deque.offer(x.left);deque.offer(x.right);}else if(x.right != null){return false;}else if(x.left != null){deque.offer(x.left);flag = false;}else {flag = false;}}else {Node x = deque.poll();if(x.left != null || x.right != null){return false;}}}return true;}