一、概述

贪心法将一个复杂问题分解为一系列较为简单的局部最优解，每一步都是对当前解的一个扩展，直到获得问题的完全解。贪心法的典型应用时求解最优化问题，而且即使是非最优解，最终得出的解也和最优解比较近似

1.1 贪心法设计思想

贪心法在解决问题的策略目光上比较短浅（笑），只会根据当前的信息做出最优的选择，而不会管未来发生了什么。贪心法并不是从整体最优考虑的，他所做出的选择只是局部上的最优，这种局部最优选择并不总能获得整体最优解，但是通常可以获得近似最优解。如果一个问题的最优解只能使用穷举获得，那么贪心法是一个牺牲精度换取时间的寻找问题近似最优解的较好方法

二、图问题的贪心法

2.1 TSP问题

描述：

TSP问题是指旅行家要旅行n个城市，要求各个城市经历并且只经历一次然后回到出发城市，并且要求所走的路径最短。

解法1：

TSP问题的贪心策略可以采用最近临近点策略：从任一城市出发，在与之相邻并且没有到达的城市中选择最近的一个，直到经过了所有城市后回到初始出发城市。这种方法同时也使用在了图求单源最短路径的普利姆算法上。

分析：
算法的时间性能为O(n²)，因为执行了n-1次贪心选择，每一次贪心选择都需要查找满足贪心条件的最短边。使用该算法求解TSP问题所得结果不一定是最优解，更加多情况是一种近似解。

解法2：

思路：
TSP问题的贪心策略还可以采用最短链接策略：每次在整个图的范围内选择最短边加入解集合中，但是要保证加入解集合中的边最终新城一个哈密顿回路。在有n个结点的图中，该算法刚开始会将图的所有边都去除，变成无边的非连通图T，每个节点都是一个连通分量。算法首先使用一个线性表存储边的信息（包括连接哪两个节点，边的权值信息），然后从小到大排序。算法会按权值从大到小遍历该线性表，不断选取当前未被选取并且权值最小的边，如果这个边连接的两个顶点落在两个不同的连通分量上的时候，证明该边可以沟通两个连通分量，将两个连通分量变成一个连通分量，那么就将这个边加入到T中；否则跳过继续遍历下一个边。以此类推直到所有节点都在一个连通分量上。最后只需要将度只有1的顶点和起始顶点连接，就得出了最终解。

分析：
该算法执行了n-1次贪心选择，在每一次贪心选择中，如果顺序查找最短边，那么时间复杂度为O(n^2)。如果采用堆排序的方法对未选择的边建立小顶堆，那么可以将时间复杂度提高到O(n*long₂n)。

2.2 图着色问题

问题：
给定无向连通图G=(V,E)，图着色问题要求使用k种颜色对图G中的顶点进行着色，需要使任意两个相邻的顶点颜色不同，求k的最小值是多少。

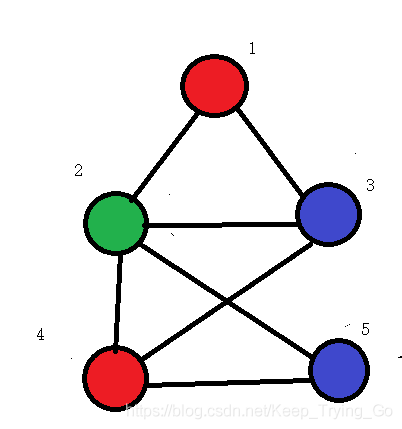
思想：
假设k个颜色的集合为{1,2…k}，一种贪心算法是选择一种颜色，然后使用改颜色尽可能多地将顶点着色，也就是选择颜色1，遍历图中未被着色的各个顶点，如果某定点可以用颜色1着色，也就是它相邻的顶点颜色都不是颜色1，那么就将它着色。一次遍历后再选择颜色2重复上述过程，直到所有的顶点都已经被着色。

分析：
该方法需要试探k种颜色，每种颜色都需要遍历所有顶点进行冲突测试，设图有n个结点，那么他的时间复杂度为O(k*n)。需要说明的是，贪心法求解图着色问题得到的不一定是最优解，在二部图中，当i为奇数的时候，顶点i和除了顶点i+1之外的所以顶点相连；当i为偶数的时候顶点i和除了顶点i-1之外的所有顶点相连。这样的图称之为二部图，在二部图中，顶点可以被划分为两个集合：编号为奇数的顶点划分到集合v，编号为偶数的顶点划分到集合u。

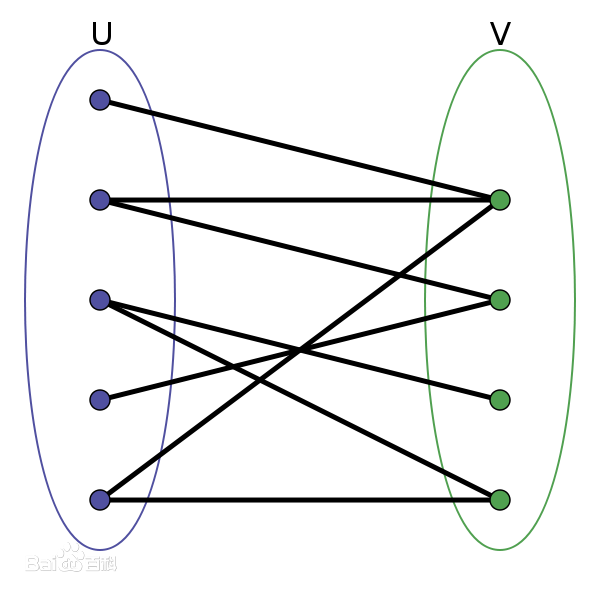
显然，二部图只需要两种颜色就可以完成着色，但是按照贪心着色法，需要使用n种颜色进行着色。

2.3 最小生成树问题

详情请见数据结构中的克鲁斯卡尔算法和普利姆算法
https://blog.csdn.net/weixin_45434953/article/details/127459188

三、组合问题中的贪心法

3.1 背包问题

问题描述：
给定n种物品和一个背包，物品i的重量为w_i，其价值为v_i，背包容量为C，如何选入装入背包的物品，使得装入背包中物品的总价值最大？

思想：
用贪心法求解背包问题的关键是如何确定贪心策略，使得按照一定次序选择装入物品，直到背包装满。常用的贪心策略有三种：

1. 选择价值最大的物品，但是可能会导致背包容量消耗过快
2. 选择重量最轻的物品
3. 综合以上两种策略，选择性价比最高的物品，也就是使用价值/重量，选出单位价值最大的物品。

贪心策略3往往是最容易得出近似最优解的策略，而策略3的主要时间消耗来自于需要将各物品按照单位重量价值进行排序，因此其时间复杂度为O(n*log₂n)，贪心法无法得出0-1背包问题的最优解，因为物品不允许分割，部分闲置的背包容量浪费了，因此0-1背包问题的最佳解法还是使用动态规划法

3.2 活动安排问题

问题：
设有n个活动集合E={1,2…n}，其中每个活动都要求使用统一资源，而同一时间内只有一个活动能够使用该资源，每个活动i都有一个起始时间si和一个结束时间fi，如果选择了将资源分配给活动i，那么活动i将会在$[s_i,f_i）$内占用该资源。如果两个活动的时间区间不相交，则称两个活动是相容的。活动安排问题要求在所给出的活动中选出最大的相容活动子集，也就是尽可能安排更多的活动

思想：
贪心法求解活动安排问题的关键是如何选择贪心策略，使得按照一定顺序选择相容活动，并且能够安排尽量多的活动，一般使用的贪心策略是：贪心地选择最早结束的活动，这样可以使得下一个活动尽早开始。这种贪心选择的目的是使得剩余时间最大化，以便安排尽可能多的相容活动。为了在每一次贪心选择时快速查找具有最早结束时间相容活动，可以将n个活动按照结束时间非减续排列。

算法分析：
各个活动按照结束时间从小到大排序，使用快速排序其时间代价是O(nlog₂n)。然后依次考察活动的代价是O(n)，因此总的时间复杂度为O(nlog₂n)。

3.3 多机调度问题

问题：
设有n个独立作业{1,2…n}，由m台相同的机器{M₁,M₂,…M_m}进行加工处理，作业i所需的处理时间为t_i，每个作业都可以在任何一机器上，但是不可以间断和拆分。多机调度问题要求是的所给的n个作业在尽可能短的时间内使用m台机器加工完成。

想法：
贪心法求解多机调度问题的贪心策略是最长处理时间作业优先，也就是将处理时间最长的作业分配给最先空闲的机器，这样可以保证处理时间长的作业优先处理，从而在整体上获取尽可能短的处理时间。

分析：
首先使用快排进行排序，时间性能为O(nlog₂n)，然后完成前m个作业，时间性能为m。通常时间复杂度为O(nxm)