【题目链接】

ybt 1216：红与黑
OpenJudge NOI 2.5 1818:红与黑

【题目考点】

1. 搜索 连通块问题

【解题思路】

1. 深搜

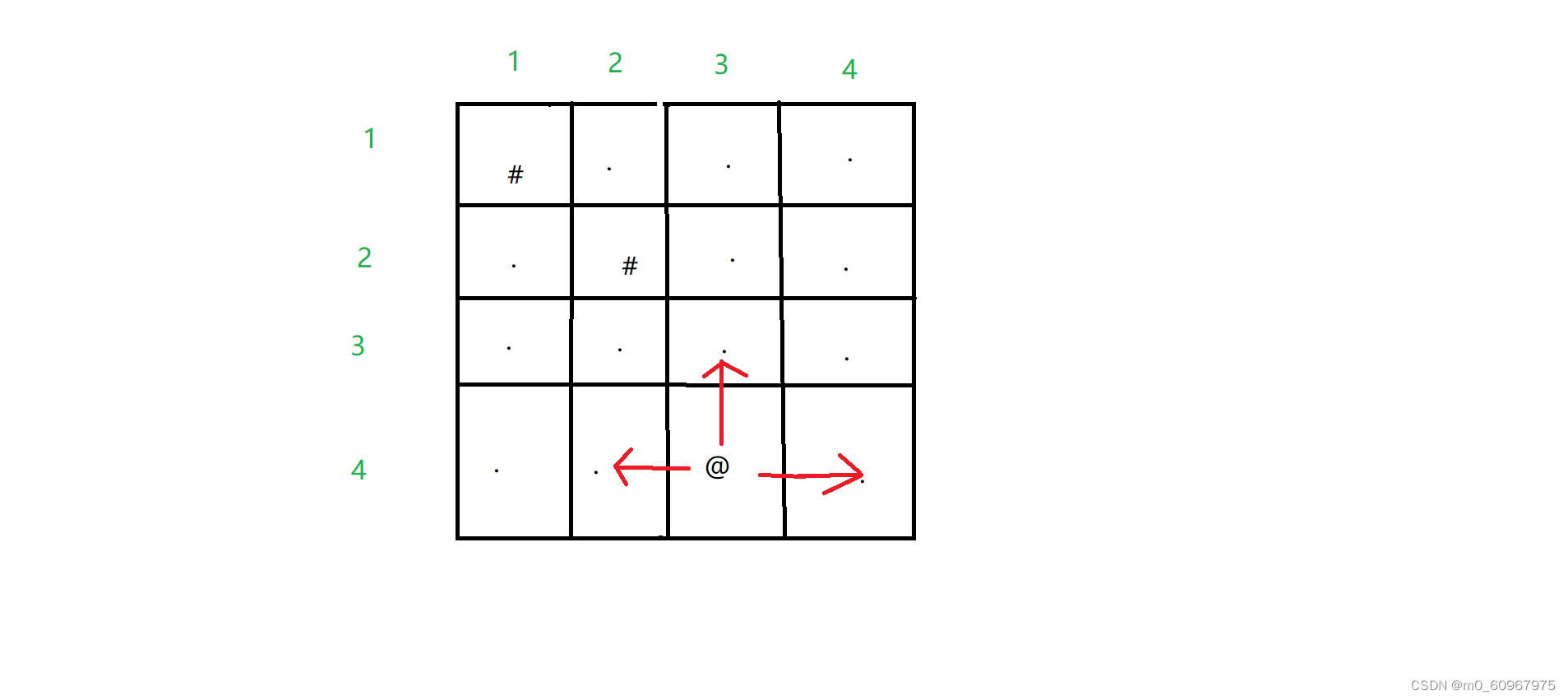
从第一个格子出发，遍历所有可以前进的方向，前进到下一个格后，再遍历可以前进的方向，走过的格子做标记，标记过的格子就不走了，不是黑色的格子不走。如果没有可以走的格子，那么退回到上一位置，看其它前进方向的格子可不可以走。
每走一个格子，格子计数加1，如果退回，也不减少格子计数。深搜结束后，输出格子计数。

2. 广搜

将起始位置做标记，而后入队。每出队一个位置，看看能从这个位置走到哪些位置，可以走到的位置必须满足3个条件：在地图内，没标记过，是黑色格子。将能从该位置走到的位置做标记，而后入队。继续出队一个位置，循环此过程，直到队空。
每标记一个位置，格子计数加1。广搜结束后，输出格子计数。

【注意】：该题中，w表示宽度，也就是列数。h表示高度，也就是行数。这是一个h行w列的矩阵。

【题解代码】

解法1：深搜

#include <bits/stdc++.h>
using namespace std;
#define N 25
char mp[N][N];//地图
int w, h, ct;//h:行数，w:ct:结果计数
int dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};//方向数组
bool vis[N][N];
void dfs(int sx, int sy)
{for(int i = 0; i < 4; ++i){int x = sx + dir[i][0], y = sy + dir[i][1];if(x >= 1 && x <= h && y >= 1 && y <= w && vis[x][y] == false && mp[x][y] != '#'){ct++;vis[x][y] = true;dfs(x, y);}}
}
int main()
{int stx, sty;//起始位置while(true){cin >> w >> h;if(w == 0 && h == 0)return 0;for(int i = 1; i <= h; ++i)for(int j = 1; j <= w; ++j){cin >> mp[i][j];if(mp[i][j] == '@')stx = i, sty = j;}memset(vis, 0, sizeof(vis));//多组数据，注意状态还原ct = 1;vis[stx][sty] = true;dfs(stx, sty);cout << ct << endl;}return 0;
}

解法2：广搜

#include <bits/stdc++.h>
using namespace std;
#define N 25
struct Node
{int x, y;Node(){}Node(int a, int b):x(a),y(b){}
};
char mp[N][N];//地图
int w, h;//w：列数 h：行数
int dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};//方向数组
bool vis[N][N];
int bfs(int sx, int sy)//传入起始位置
{queue<Node> que;vis[sx][sy] = true;que.push(Node(sx, sy));int ct = 1;//计数，看可以到达几个黑色格子while(que.empty() == false){Node u = que.front();que.pop();for(int i = 0; i < 4; ++i){int x = u.x + dir[i][0], y = u.y + dir[i][1];if(x >= 1 && x <= h && y >= 1 && y <= w && vis[x][y] == false && mp[x][y] != '#'){vis[x][y] = true;que.push(Node(x, y));ct++;}}}return ct;
}
int main()
{int stx, sty;while(true){cin >> w >> h;if(w == 0 && h == 0)return 0;for(int i = 1; i <= h; ++i)for(int j = 1; j <= w; ++j){cin >> mp[i][j];if(mp[i][j] == '@')stx = i, sty = j;}memset(vis, 0, sizeof(vis));cout << bfs(stx, sty) << endl;}return 0;
}