【题目描述】
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻的黑色瓷砖移动。请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
【输入】
包括多组数据。每组数据的第一行是两个整数W和H,分别表示x方向和y方向瓷砖的数量。W和H都不超过20。在接下来的H行中,每行包括W个字符。每个字符表示一块瓷砖的颜色,规则如下:
1)‘.’:黑色的瓷砖;
2)‘#’:白色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每组数据中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
【输出】
对每组数据,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
【输入样例】
6 9 ....#. .....# ...... ...... ...... ...... ...... #@...# .#..#. 0 0
【输出样例】
45
题解:
这题是一个类似经典深搜走迷宫问题(其实广搜也可以)
首先
输入得用while循环,终止条件是m==0||n==0。输入的时候发现‘@’(起点)那么存下标,之后dfs:
int x=0,y=0;cin>>m>>n;while(m!=0&&n!=0){ans=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];if(a[i][j]=='@'){x=i;//记录起点y=j;}}}dfs(x,y);//深搜cout<<ans+1<<endl;//因为起点也算cin>>m>>n;}然后:
写dfs:
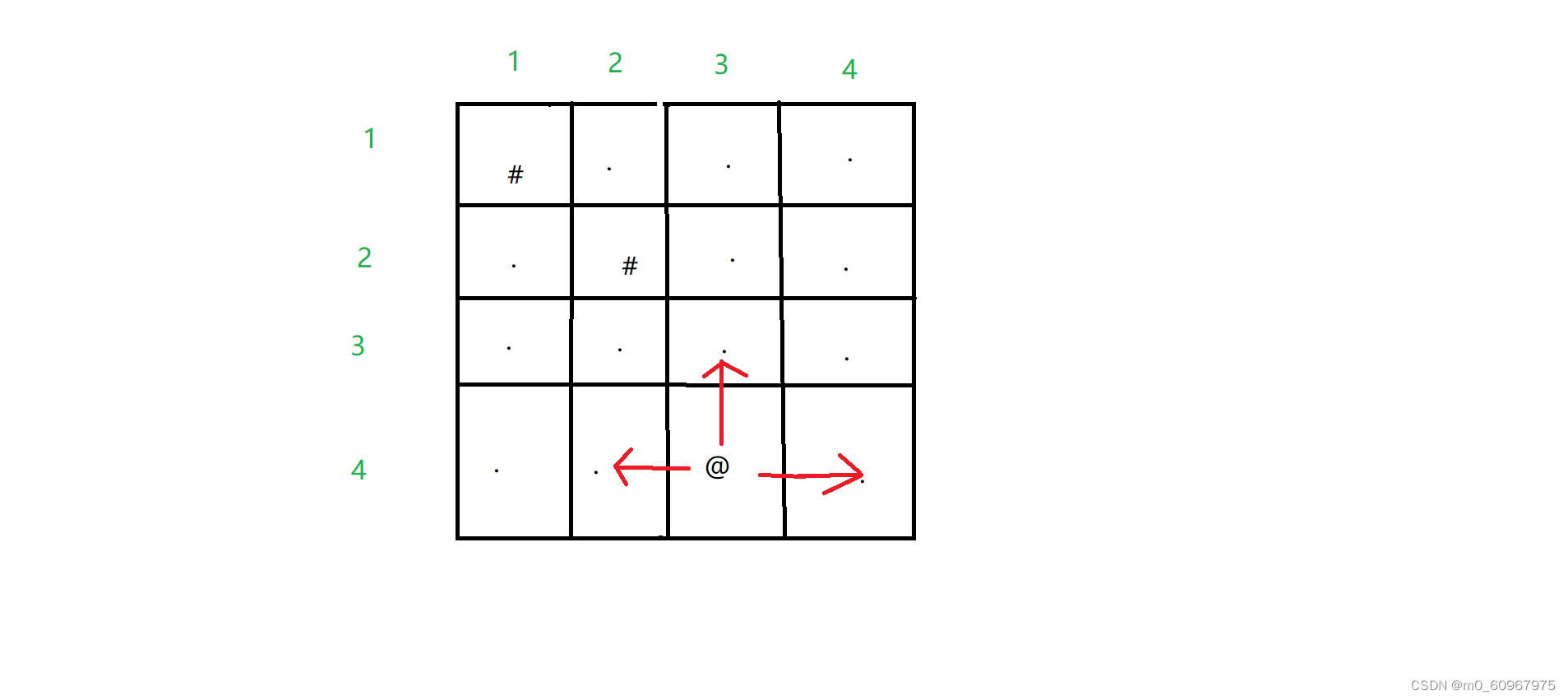
如图4×4的矩阵4行3列为起点,本可向上下左右走,但因下面为边界,所以下不能走。而走过的瓷砖得标记,下次再走的时候ans就不加一了。如图3行2列的‘.'向上是’#‘不能走,所以移动时得判断这个方向是否可走:
int qx[]={1,0,-1,0};
int qy[]={0,1,0,-1};
void dfs(int x,int y)
{for(int i=0;i<4;i++){int xx=x+qx[i];int yy=y+qy[i];if(xx<1||xx>n||yy<1||yy>m){continue;//越界}if(a[xx][yy]=='.'){ans++;a[xx][yy]='!';//标记为走过dfs(xx,yy);}}
}不管你懂不懂,把总代码给你们看:
#include<bits/stdc++.h>
using namespace std;
int m,n,ans;
char a[1001][1001];
int qx[]={1,0,-1,0};
int qy[]={0,1,0,-1};
void dfs(int x,int y)
{for(int i=0;i<4;i++){int xx=x+qx[i];int yy=y+qy[i];if(xx<1||xx>n||yy<1||yy>m){continue;}if(a[xx][yy]=='.'){ans++;a[xx][yy]='!';dfs(xx,yy);}}
}
int main()
{int x=0,y=0;cin>>m>>n;while(m!=0&&n!=0){ans=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];if(a[i][j]=='@'){x=i;y=j;}}}dfs(x,y);cout<<ans+1<<endl;cin>>m>>n;}return 0;
}